
5.3. Влияние поперечной деформации εу на профиль продольной скорости
Вертман [139, 140, приложение] рассмотрел частный случай трехмерной деформации в шельфовом леднике. Для двухмерного случая, т. е. при нулевой боковой деформации 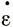 у = 0,
у = 0,
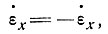
Вертман получил
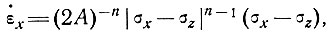
(1)
а для случая шельфового ледника, расширяющегося одинаково во всех горизонтальных направлениях (три измерения), -
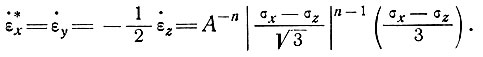
(2)
Заметим, что
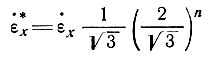
и, поскольку 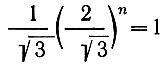 при n ≈ 4, получаем интересный результат - скорость продольной деформации для данного девиатора напряжения уменьшается при наличии равного бокового растяжения при малых значениях n (<4), в то же время при больших значениях n скорость должна возрастать.
при n ≈ 4, получаем интересный результат - скорость продольной деформации для данного девиатора напряжения уменьшается при наличии равного бокового растяжения при малых значениях n (<4), в то же время при больших значениях n скорость должна возрастать.
Теперь рассмотрим влияние на скорость продольной деформации  х скорости произвольной поперечной деформации
х скорости произвольной поперечной деформации  у. Примем закон течения в виде
у. Примем закон течения в виде
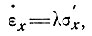
(4)
где
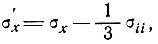
(5)
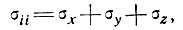
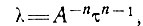
(6)
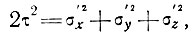
(7)
здесь τ - эффективное напряжение сдвига, равное 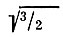 октаэдрического напряжения сдвига, А и n - параметры степенного закона течения.
октаэдрического напряжения сдвига, А и n - параметры степенного закона течения.
Теперь необходимо определить скорость деформации 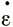 х выраженную через продольные и вертикальные напряжения σх, σz и скорость поперечной деформации
х выраженную через продольные и вертикальные напряжения σх, σz и скорость поперечной деформации 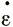 у. Из выражений (4) и (5) получаем
у. Из выражений (4) и (5) получаем
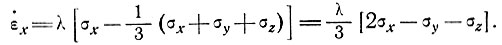
(8)
Значение σу находим по формулам:
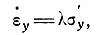
(9)
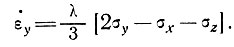
(10)
Следовательно
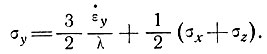
(11)
Подставив это выражение в уравнение (8), получаем
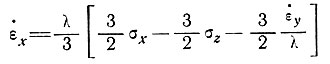
или

Затем, чтобы получить значение λ из выражения (6), надо определить сначала величину τ из уравнения (7), для чего необходимы девиаторы напряжения.
Решая уравнения (4) и (12), находим
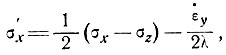
(13)
аналогично-
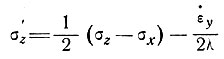
(14)
и
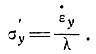
(15)
Отсюда, по формуле (7), получаем
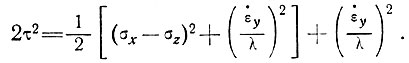
(16)
Теперь запишем скорость боковой деформации как некоторую часть (скажем, γλ) от разности напряжений σх - σу, т. е.
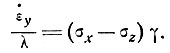
Тогда из уравнения (12) следует
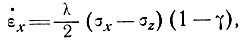
(18)
а из уравнения (16) -
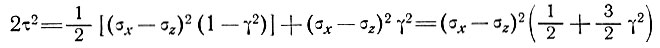
(19)
или
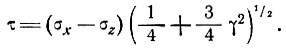
(20)
Заменим этим выражением параметр τ в уравнении (6), чтобы получить величину λ, которую мы можем подставить в формулу (18) для скорости продольной деформации:
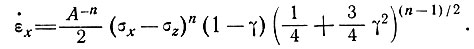
(21)
Поскольку мы хотим знать соотношение между скоростью продольной деформации 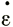 х и разностью напряжений σх - σz для данной скорости поперечной деформации
х и разностью напряжений σх - σz для данной скорости поперечной деформации 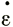 у, которая составляет некоторую часть (скажем, ν) от скорости продольной деформации, запишем
у, которая составляет некоторую часть (скажем, ν) от скорости продольной деформации, запишем
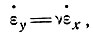
(22)
тогда из выражения (12) получим
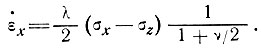
(23)
Сравнивая это выражение с уравнением (18), видим, что параметры γ и ν связаны между собой одним из следующих соотношений:
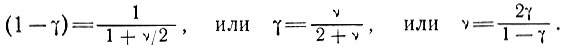
(24)
Затем, наконец, исходя из выражений (24) и (21), скорость деформации можно записать в виде
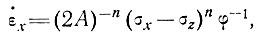
(25)
где
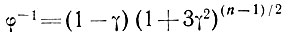
(26)
или
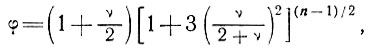
(27)
где φ - функция поперечной деформации.
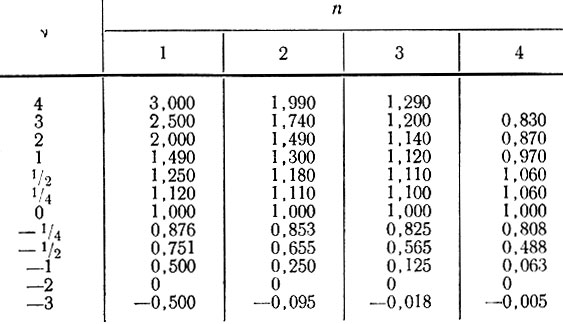
Таблица 5.1
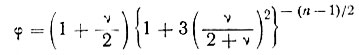
По аналогии с уравнением (1) для двух измерений, где скорость боковой деформации равна нулю, для скорости боковой деформации, которая в ν раз больше скорости продольной деформации, имеем
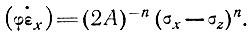
(28)
Другими словами, если поперечная деформация 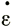 y = νεx существует, то можно учесть ее влияние, вводя величину φ1/nε1/nx вместо
y = νεx существует, то можно учесть ее влияние, вводя величину φ1/nε1/nx вместо 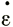 1/nx.
1/nx.
Таблица 5.2
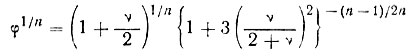
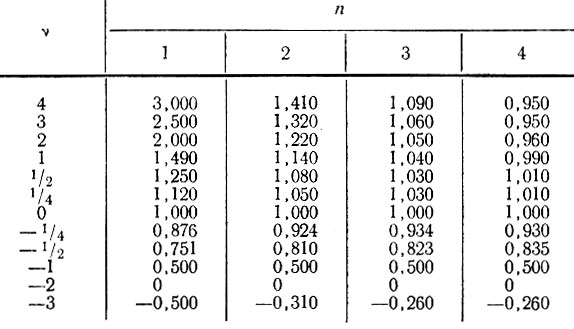
Значения функций φ и φ1/n при различных значениях ν и n приведены в табл. 5.1 и 5.2. Они иллюстрируются рис. 5.1 и 5.2. По данным таблиц видно, что для закона течения при n, равном 3 или 4, наличие скорости боковой деформации не вызывает существенных изменений. Даже значения ν, составляющие +1, +2, + 3, вызывают лишь небольшие изменения при больших значениях n. При n, равном 1 или 2, отклонения становятся более значительными.
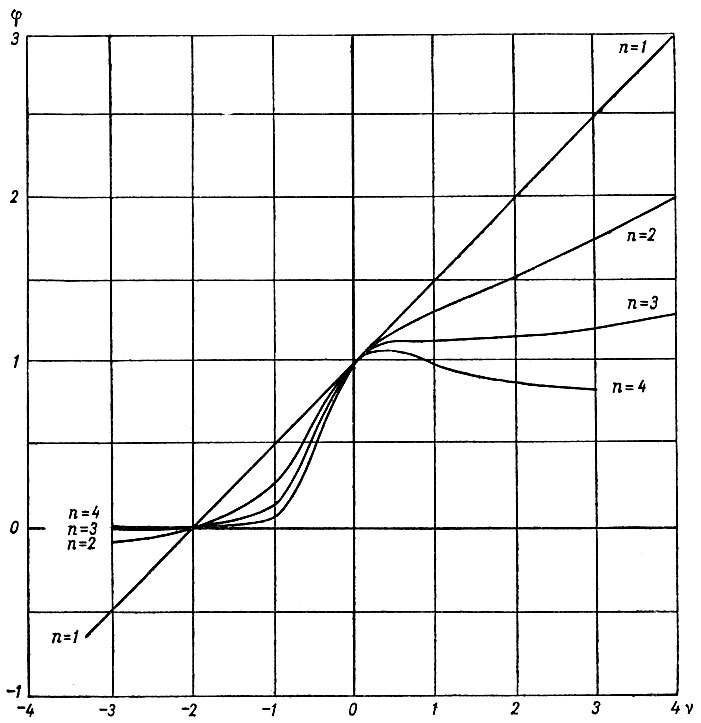
Рис. 5.1. Зависимость функции φ(ν, n) поперечной деформации от величин ν и n
Однако, когда боковая деформация имеет обратный знак, отклонения становятся очень существенными. В частности, для ν = -2 находим, что разность продольных напряжений равна нулю. Это прямо следует из условия неразрывности для несжимаемой среды:
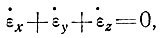
и, если
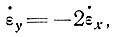
то
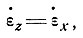
т. е. скорость продольной деформации может существовать даже при σх - σz = 0.
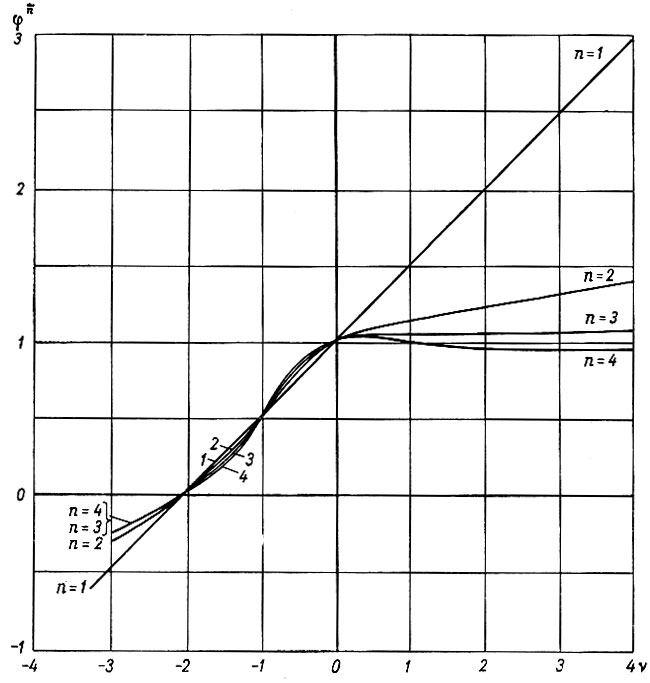
Рис. 5.2. Зависимость функции φ1/nn(ν) продольной деформации от величин ν и n
Это означает, что при ν = -2 боковое движение преобладает над продольным и вызывает равные вертикальные и продольные деформации, приводящие к сохранению объема. При больших отрицательных значениях ν (-3, -4, . . .) разность средних продольных напряжений имеет знак, противоположный знаку скорости продольной деформации.
Таким образом, наше общее уравнение движения для трех измерений теперь может быть записано в виде
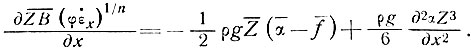
(29)
Кроме того, мы можем связать продольный наклон α со скоростью продольной деформации 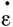 х и учесть влияние функции поперечной деформации φ. Рассмотрение следствий этого для некоторых типов масс льда будет осуществлено в разделе 6.
х и учесть влияние функции поперечной деформации φ. Рассмотрение следствий этого для некоторых типов масс льда будет осуществлено в разделе 6.
|
ПОИСК:
|
© GEOMAN.RU, 2001-2021
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'