5.4. Течение льда по волнообразному ложу

5.4.1. Коротковолновые колебания. Бентли [11], Робинсон [117], Бадд [17], Робин [116] и Мок [81] приводили много примеров волнообразного характера поверхности холодных ледниковых куполов. Механизм образования волн на поверхности ледовых масс обсуждался Вертманом [141] и Наем [88 - 90]. Общая теория этих зависящих от времени волн весьма сложна и здесь не рассматривается.

В настоящей работе влияние нерегулярности ложа на течение льда до сих пор не затрагивалось, так как наклон основания ??? в явном виде не входил в окончательные уравнения скорости продольной деформации. Однако уравнения, полученные для продольной скорости и скорости деформации, могут использоваться для изучения установившегося течения по волнообразному ложу.

Рассмотрим недивергентное двухмерное течение куполового ледника вниз по небольшому, установившемуся наклону β₀.

В общем случае ложе шероховатое и не носит регулярного характера. Здесь же для рассмотрения течения ледника по волнообразному ложу принимаются следующие допущения.

Допущение 1.

(1)

где β₀ - региональный наклон, β₁ - амплитуда колебаний угла наклона и ω частота колебаний подстилающей поверхности вдоль линии движения х. Можно ожидать, что действительные формы ложа могут быть аппроксимированы суперпозицией различных мод колебаний.

Сначала рассматривается лишь простейший вид установившегося течения, однако возможны некоторые обобщения, выполненные в дальнейшем.

Допущение 2. Средняя толщина льда по региону незначительно меняется над волнообразной подстилающей поверхностью, причем градиент толщины льда определяется выражением

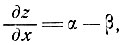
(2)

где α - наклон поверхности.

Допущение 3. Предположим, что наклон поверхности определяется следующим образом:

(3)

где α - постоянный региональный наклон, α₁ и α₂ - константы, подлежащие определению.

Допущение 4. Скорость аккумуляции А постоянна вдоль волнообразной поверхности.

Допущение 5. Изменения в толщине льда z и средняя горизонтальная скорость во льду V малы по сравнению с аналогичными величинами в данном регионе.

Допущение 6. Исходя из результата, полученного в предыдущем подразделе для низкой скорости деформации, принимаем градиент скорости деформации пропорциональным отклонению наклона поверхности от общего регионального наклона, т. е. в соответствии с уравнением (29) подраздела 5.1

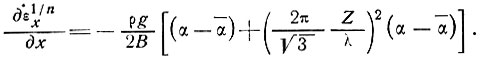
Результаты, полученные в разделе 6 (см. рис. 67), предполагают, что для небольших скоростей продольной деформации можно принять n = 1

или

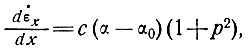
(4)

где

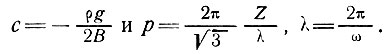
Условие неразрывности требует, чтобы

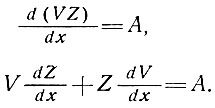
(6)

Из уравнений (1), (2) и (3) имеем

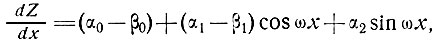
(7)

а из уравнений (3) и (4) -

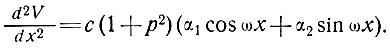
Следовательно,

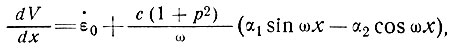
поскольку р можно считать константой, при условии, что 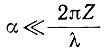. Подставляя выражения (9) и (7) в уравнение (6), видим, что допущение 3 совместимо с допущением 1 и условием неразрывности установившегося состояния, если

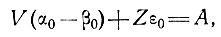
(10)

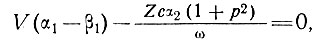
(11)

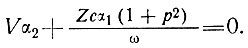
(12)

Уравнение (10) является уравнением неразрывности для региональных (сглаженных) величин, независимых от колебаний ложа в данной области. Остальные уравнения определяют колебания поверхности в величинах колебаний ложа и других параметров: толщины льда Z, скорости V, длины волны λ и параметра "вязкости" В.

Из уравнения (12) получаем

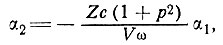
(13)

а из уравнения (11) -

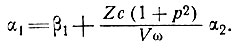
(14)

Подставляя в последнее уравнение значения из уравнения (13), получаем

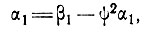
где

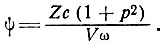
(15)

Следовательно,

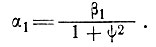
(16)

Отсюда и из выражения (13) находим

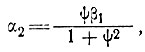
(17)

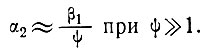
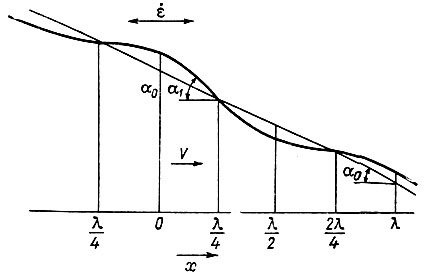
При φ >1 из уравнений (16) и (17) следует, что колебания поверхности не совпадают по фазе с колебаниями ложа. Когда φ 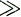1, расхождение колебаний по фазе составляет π/2, а максимальный наклон поверхности имеет место над высшей точкой ложа. Это означает, что наклоны поверхности совпадают по фазе с выступами ложа. Из уравнений (16) и (17) очевидно, что поверхностные волны всегда меньше, чем волны ложа, т. е. они демпфируются с коэффициентом φ, который можно назвать коэффициентом демпфирования.

Выражая φ из уравнений (5) и (15), получаем

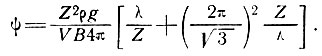
(18)

Эта функция имеет минимум при длине волны

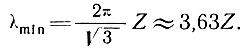
(19)

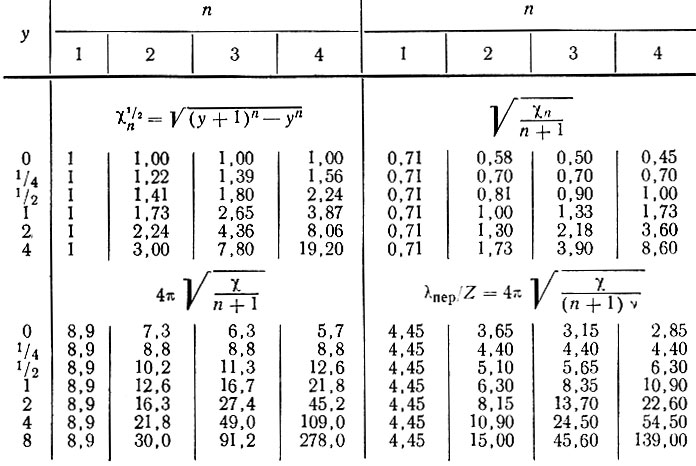
Это означает, что колебания ложа с длиной волны, превышающей примерно в три-четыре раза толщину льда, меньше демпфируются, чем при других длинах волн. Однако по данным табл. 5.3 видно, что φ не является быстро меняющейся функцией λ, особенно при больших значениях, чем λmin. Представляется, что волны с меньшим периодом быстро демпфируются, а волны с большими периодами демпфируются лишь немногим быстрее. Это приводит к появлению большого числа гармоник, т. е. волны длиной 2λmin, 3λmin или 4λmin могут преобладать, особенно когда они накладываются на более короткие волны.

Таблица 5.3

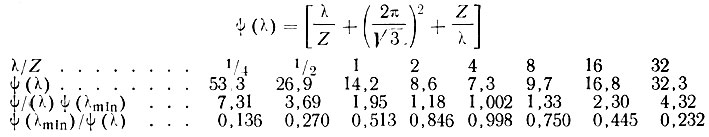
Из уравнений (17) и (18) очевидно, что большая толщина льда вызывает большее демпфирование колебаний поверхности. Если другие параметры остаются неизменными, то при более высоких скоростях, а также более высоких значениях параметра вязкости В демпфирование меньше. Параметр В можно оценить по относительным амплитудам колебаний ложа и поверхности следующим образом:

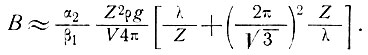
(20)

Оценку порядка величины демпфирования можно получить, если вспомнить, что из уравнения (40) подраздела 5.1 имеем

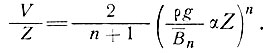
(21)

При n = 1

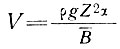
или

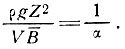
Если обозначить через 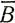₁ величину 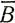_n из уравнения (21), выраженную в единицах, соответствующих n = 1, с помощью общего уравнения [16, 17]

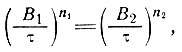
(22)

тогда выражение (21) может быть записано в виде

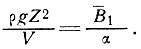
Отсюда φ из уравнения (18) выразится следующим образом:

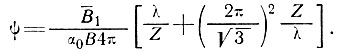
(23)

Здесь α₀ - региональный наклон, причем его типичные величины изменяются в пределах от 10^-3 до 10^-1. Величина В в знаменателе взята из уравнений (4) и (5). Она характерна для продольной деформации по всей толщине льда. Параметр В₁ в числителе - величина, характерная для базисных слоев (в единицах, соответствующих величинам при n = 1). При высокой температуре в этих слоях она может быть на порядок меньше. Следовательно, можно ожидать, что типичное демпфирование уменьшается в 2 - 100 раз в направлении к побережью, по мере того как средний наклон поверхности возрастает. Коэффициенты демпфирования колебаний ложа и поверхности куполового ледника Уилкса будут рассмотрены в п. 6.3.5 и использованы при расчете параметра течения В.

Распространение анализа на случаи трехмерных возмущений ложа можно осуществить введением коэффициента поперечной деформации φ из уравнения (28) подраздела 5.4 и обобщения уравнения неразрывности. Чистым результатом при равной скорости поперечной деформации является увеличение демпфирования с коэффициентом ⁴/₃ при низких скоростях деформации (n = 1). По нормали к линии тока волны поверхности и ложа находятся в фазе. Следовательно, для направлений, лежащих между линией тока и нормали к линии тока разность фаз между наклоном поверхности и высотой ложа изменяется от 0 до - π/2.

Как это было установлено Блэком и Баддом [13], вышеприведенный анализ аналогичным образом может быть распространен на случай переменной скорости аккумуляции на волнообразной поверхности. В этом случае можно записать

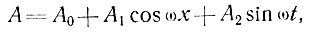
и тогда вместо уравнений (16) и (17) получаем:

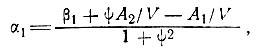
(16')

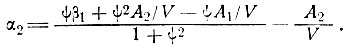
(17')

При φ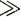1

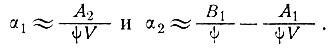
Отсюда следует, что при больших значениях φ, являющихся результатом больших скоростей деформации, или малых значениях В аккумуляция не изменяется в больших пределах.

Блэк и Бадд [13] установили, что максимумы аккумуляции наблюдались около мест, где наклон поверхности минимален. Этот эффект становится важным при малой величине φ или больших значениях В, что является причиной малых скоростей деформации.

Положив φ→0 в уравнениях (16') и (17'), получаем:

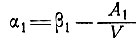
(16")

и

(17")

Отсюда при низкой скорости деформации характер аккумуляции может стать очень существенным при определении конфигурации поверхности в установившемся состоянии.

5.4.2. Длинноволновые колебания. Переходя к большим масштабам и принимая сглаженные величины параметров на расстоянии, примерно в 20 раз большем толщины льда, возьмем вместо уравнения (4) соотношение, связывающее скорости V, толщину Z и наклон поверхности α льда, из формулы (40) подраздела 5.1 в виде

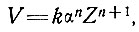
(24)

где

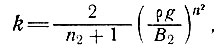
n₂≈3 и k можно считать константой при условии, что температуры на всем рассматриваемом расстоянии изменяются незначительно.

Аналогично анализу, изложенному в п. 5.4.1, принимаем:

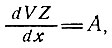
(25)

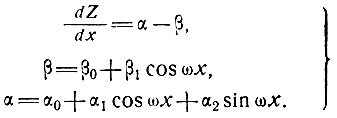
(26)

Тогда подстановка уравнения (26) в уравнение (25) дает:

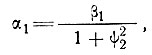
(27)

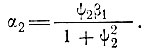
(28)

Как и ранее, колебания поверхности и основания будут иметь сдвиг по фазе, равный π/2. В этом случае коэффициент демпфирования ???2 определяется как

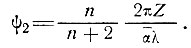
(29)

Этот результат означает, что демпфирование увеличивается с толщиной льда, уменьшается с уменьшением длины волны и обратно пропорционально наклону поверхности (табл. 5.4).

Таблица 5.4

При более общей форме изменений ложа подставляем уравнения (24) и (26) в уравнение (25) и получаем:

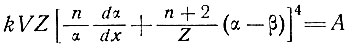
(30)

или

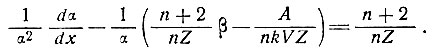
(31)

Теперь, если допустить, что изменения Z и V малы по сравнению с их средними значениями по всей области, это уравнение может быть записано в виде

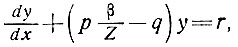
(32)

где у = ¹/₂ и р, q и r - константы. Интегрируя это выражение, получим

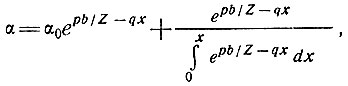
(33)

где b - высота ложа относительно точки при х = 0. Здесь не будет обсуждаться значение этого уравнения в целом, но, рассматривая профиль ложа с колебаниями вида b = b₀ + b₁ cosωx, можно показать, что уравнение (33) предполагает слегка более удлиненную поверхность, чем поверхность правильной синусоидальной формы, т. е. что ее пики короче, а впадины длиннее.

5.4.3. Масштабы расстояний, соответствующие длинноволновым и коротковолновым колебаниям. В крупном масштабе при сглаженных значениях скорости V, наклона α и толщины ледника Z имеем уравнение (21) подраздела 5.4

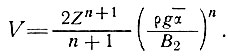
(34)

Для мелкомасштабных колебаний, где скорости деформации так малы, что напряжение и скорость деформации связаны линейно (n = 1), из уравнения (4) подраздела 5.4 имеем

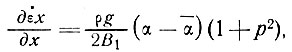
(35)

где 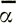- средний региональный наклон. Нам нужно найти расстояние, на котором можно "сгладить" величину 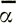в уравнениях (34) и (35). При длинноволновых колебаниях значением р можно пренебречь.

По мере увеличения длины волны колебаний λ отношения (34) и (35) становятся взаимосвязанными и уравнение (35) постепенно будет заменено уравнением (28), поскольку

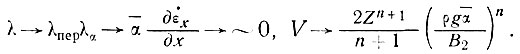
Эта замена возможна, когда увеличение скорости от вершины волны к точке максимального наклона вследствие скорости деформации, согласно формуле (35), будет равно увеличению скорости в этом интервале вследствие увеличения значений наклона из выражения (34), т. е. когда интегралы

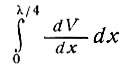
из уравнений (34) и (35) равны.

Предполагается, что наклон колебаний

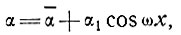
(36)

где

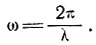
Из выражения (34) для сглаженного наклона имеем

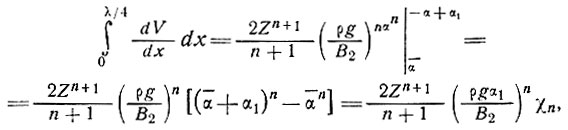
(37)

где

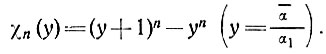
(38)

Из уравнений (35) и (36) для коротковолновых колебаний находим

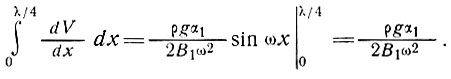
(39)

Приравнивая выражения (37) и (39), получаем

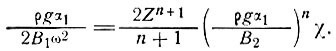
Теперь параметры В₁ и В₂ выражены соответственно в бар/с и бар/с^1/n, т. е.

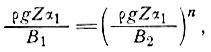
при условии, что после приведения к одинаковым единицам В₁ = В₂, например, В_к для колонки и В_осн для основания, когда n = 1. Для случая, когда они не равны, что обычно имеет место для типичных профилей температуры, существующих в холодных куполовых ледниках, где В_к > В_осн, запишем

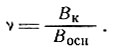
Тогда

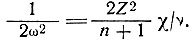
(40)

Поэтому переходная длина волны λ_пер выражается следующим образом:

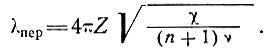
(41)

Для куполового ледника Уилкса было найдено, что (см. подраздел 6.3) ν ≈ 4 (табл. 5.5), n ≈ 3,4, а типичное значение -α/α₁ = 4. Следовательно, как можно видеть по данным табл. 5.5, переходная длина волны примерно в 30 раз больше толщины льда для этого региона.

Таблица 5.5

Результаты этого раздела показывают, что во избежание несоответствий в уравнении (34) для сглаженных величин скорости и наклона необходимо усреднять их значения по расстоянию, большему, чем величина λ_пер. С другой стороны, можно ожидать, что уравнение флуктуаций деформации и наклона

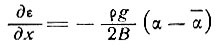
будет справедливо только при 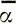, взятом сглаженным на расстоянии, большем, чем λ_пер, и при флуктуациях наклона по расстоянию, меньшему, чем λ_пер.