5.2. Трехмерный поток

Уравнения скорости для массы льда, медленно движущейся в трех измерениях вниз по склону под действием своего собственного веса, аналогичны уравнениям (4) и (5) подраздела 5.1:

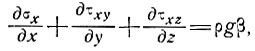
(1)

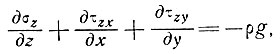
(2)

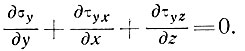
(3)

Допущение 1. Изменения формы поперечного сечения и ширины массы льда вдоль линии тока достаточно малы и ими можно пренебречь. Тогда основными изменениями в массе льда вдоль линии тока будут изменения по толщине Z и наклону поверхности α.

Поскольку канал, в котором течет ледник, не расходящийся, то составляющие скорости перпендикулярны к линиям тока, и поэтому

и

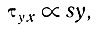
где s - коэффициент формы, который постоянен для определенной конфигурации: полукруглого поперечного сечения, бесконечно широкого поперечного сечения, бесконечно глубокого поперечного сечения, но, вообще говоря, является функцией у и z. В данном случае предположим, что s не зависит от х. Отсюда

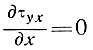
и из уравнения (3)

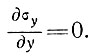
Уравнение (2) приводится к эквивалентному уравнению (6) подраздела 5.1 для двух измерений.

Проинтегрируем уравнение (1) по площади поперечного сечения и получим

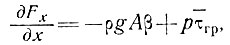
(4)

где Fx - полная сила по поперечному сечению в линии тока, р - периметр границ и 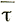_гр - среднее напряжение сдвига в пределах границ, определяемых формулой

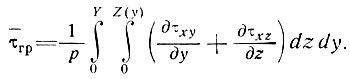
(5)

Интегрируя уравнение (2) по поперечному сечению и используя допущение 1, получим

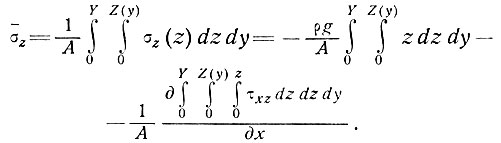
(6)

Допущение 2. Примем в первом приближении, что аналогично уравнению (23) подраздела 5.1 справедливо равенство

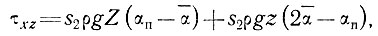
(7)

где s₂ - второй коэффициент формы, постоянный по поперечному сечению.

В разделе 3 было показано, что хотя эта аппроксимация, вообще говоря, приемлема лишь вблизи центральной линии, она достаточно справедлива для прямоугольных поперечных сечений, а также для масс льда, широких по сравнению с их толщиной. Для других поперечных сечений необходимо учитывать изменение характера поперечного сечения ледника, т. е. s₂. Мы рассмотрим лишь случай наклона α, постоянного по всему поперечному сечению.

Теперь уравнение (6) можно записать как

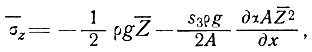
где черта означает среднее значение по сечению, т. е.

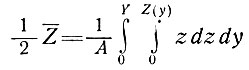
и

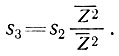
Среднее продольное напряжение определяется выражением

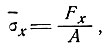
и, согласно уравнению (4), равно

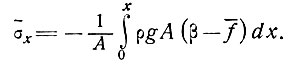
(9)

Коэффициент трения f принимаем равным

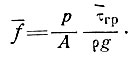
(10)

Теперь из уравнений (8) и (9) находим девиатор среднего напряжения:

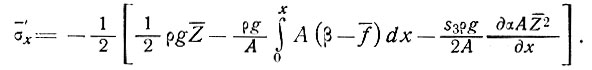
(11)

Откуда

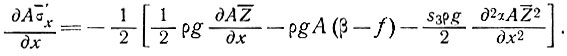
(12)

Принимая закон течения в виде

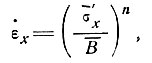
(13)

аналогичном случаю из двух измерений, где 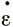_х - скорость деформации на центральной линии 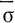и '_х и 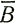- осредненные величины по сечению, и определяя 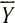через

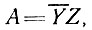
(14)

получаем уравнение (12) в виде

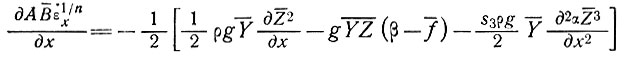
(15)

или для 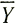= const.

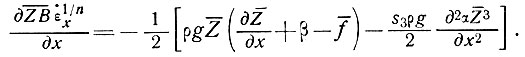
(16)

Наконец, при 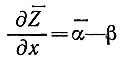и допуская, что последним членом правой части уравнения (16) в условиях, соответствующих рассмотренным для двух измерений, можно пренебречь, запишем

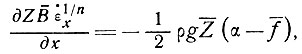
(17)

что аналогично результатам, полученным для двух измерений, причем некоторые из параметров усреднены по поперечному сечению и имеют более общий смысл. Аналогично этому можно выразить член f через величины средней скорости или скорости на центральной линии, используя приближенные коэффициенты формы в том виде, в каком они были рассчитаны для конкретных поперечных сечений Наем [92, 93]. Это позволяет распространить результаты двух измерений, полученные в разделе 3, на массы льда, ограниченные с боков, такие, как типичные глетчеры или шельфовые ледники, при условии, что поперечные растяжение или сжатие пренебрежимо малы. Влияние такого конвергентного или дивергентного потока на скорость продольной деформации и профиль скорости будет исследовано ниже.