5.1. Двухмерный поток

Рассмотрим элементарный объем, движущийся вдоль линии тока льда, где нет скоростей поперечной деформации, типичной, скажем, для центральной линии тока очень широкого по сравнению с его толщиной глетчера, имеющего параллельные стороны, или для линии тока куполового ледника, где горизонтальная дивергенция пренебрежимо мала. Мы хотим определить профиль продольной скорости и скорость деформации по изменению размеров массы льда и закону течения льда. Этот метод аналогичен методу Шумского [122 - 125], но отличается от него некоторым существенным видоизменением и в значительной мере основывается на измерениях, проведенных непосредственно в массах льда.

Бадд [18], Либутри [66], Шумский [127], Робин [115] и другие показали, что продольные напряжения имеют большое значение для движения льда. Коллинз в 1968 г. пришел к аналогичным выводам и исследовал условия, при которых справедливо приближенное уравнение Робина для скорости продольной деформации. Най доказал, что точное уравнение градиента продольного напряжения можно упростить при ориентации продольной оси координат параллельно поверхности.

В данной работе влияние продольной деформации рассматривается на основании приближенного метода Бадда [18]. Оно оказывается корректным для масс льда с небольшим наклоном поверхности. Вывод основного уравнения при произвольной ориентации осей, которое справедливо для наклонов поверхности любой величины, дан в приложении I. Главным результатом этого более общего исследования является то, что для небольших наклонов поверхности и ложа основное уравнение градиента скорости продольной деформации не зависит от ориентации продольной оси массы льда относительно поверхности или ложа.

Возьмем ортогональные оси х (параллельную осредненному ложу и направленную вдоль движения) и z (перпендикулярную поверхности).

Введем обозначения:

α - наклон поверхности в точке х,

β - наклон ложа в точке х,

z - толщина льда в точке х,

ρ - плотность льда (принимаемая постоянной),

g - ускорение силы тяжести,

τ_б - напряжение сдвига в базисном слое,

τ_х, σ_хz, σ_z - компоненты напряжения и

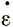 , ε_xz, ε_z - компоненты скорости деформации.

На основании результатов раздела 2 имеем следующее эмпирическое соотношение для закона течения хаотически ориентированного поликристаллического льда:

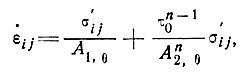
(1)

где 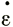_ij - тензор скорости деформации, σ_ij - девиатор напряжения, τ₀ - октаэдрическое сдвиговое напряжение, определяемое как

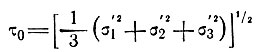
(2)

(σ'₁, σ'₂, σ'₃ - главные девиаторы напряжения);

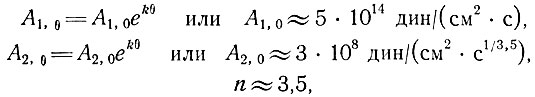
(3)

где θ - температура льда, °С, и

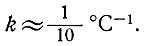
Закон течения льда можно выразить в значениях эффективного напряжения сдвига, т. е.

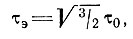
простым подбором соответствующей величины А₂. Поэтому в дальнейшем индекс у τ опускается. Заметим, что в некотором ограниченном диапазоне напряжений можно представить закон течения льда в виде

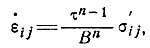
(4)

где величины n и В выбраны такими, чтобы они соответствовали кривой рис. 2.2 в заданной области. Этот вид закона течения примем в качестве общего, хотя в некоторых случаях может оказаться более удобным представить обобщенный закон течения льда в виде

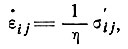
где η (τ, θ) - "обобщенная функция вязкости", зависящая как от напряжения, так и от температуры, и определяемая по формуле 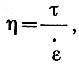, где τ и 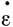- октаэдрическое сдвиговое напряжение и скорость деформации при данной температуре, устанавливаемые эмпирически по кривым зависимости скорости деформаций от напряжения (см. рис. 2.2).

Примем допущение, что наклоны ложа и поверхности достаточно малы и можно считать:

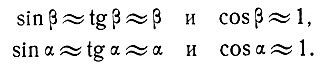
Тогда уравнения движения можно записать в виде:

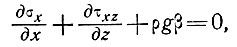
(5)

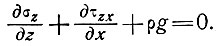
(6)

Проинтегрируем эти уравнения по ординате z, чтобы получить приближенное выражение

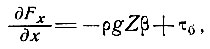
(7)

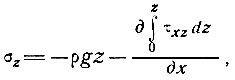
(8)

где F_x - суммарная продольная сила поперечного сечения, а τ_б - принимается положительным в направлении, противоположном течению.

В качестве основной величины, управляющей скоростью продольной деформации, нам нужен средний девиатор продольного напряжения

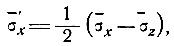
(9)

где черта - осреднение по вертикали.

Теперь

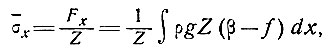
(10)

где f - коэффициент трения в базисном слое, определенный по формуле

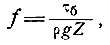
(11)

и

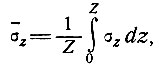
(12)

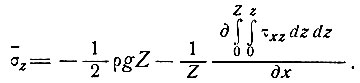
(13)

Таким образом получим

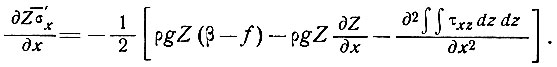
(14)

Заметим, что

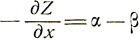
(15)

и, следовательно, уравнение (14) примет вид

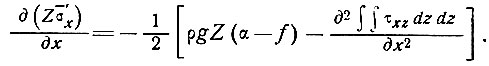
(16)

Рассматривая закон течения вида

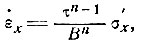
(17)

где

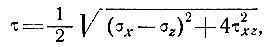
(18)

отметим, что при линейном законе течения (n = 1) скорость продольной деформации непосредственно связана с девиатором продольного напряжения, который не зависит от вертикального сдвигового напряжения τ_xz. Однако, когда действует более высокий степенной закон, вертикальный сдвиг становится существенным.

Запишем закон течения в виде

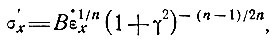
(19)

где

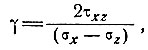
(20)

Из выражения [19] следует, что влияние вертикального сдвига τ_xz пренебрежимо мало, когда оно значительно меньше 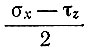или когда n ≈ 1. В подразделе 6.3 будет установлено, что действительно n ≈ 1 при скоростях продольной деформации, измеренных в куполовом леднике Уилкса.

Однако работа Картера, в которой исследуются более высокие степени сдвигового напряжения, приводит к необходимости рассмотреть влияние вертикальных сдвиговых напряжений на скорость продольной деформации (приложение II). Откуда видно, что лишь для параметра течения В₁ требуется иная интерпретация.

Последующее обсуждение затронутой темы ограничивается малыми напряжениями, а обобщение относительно участков ледниковых масс с заметным вертикальным сдвигом может быть легко осуществлено изменением интерпретации величины В₁.

Следовательно, принимаем допущение, что при вертикальном осреднении закон течения может быть записан в виде

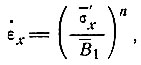
(21)

где 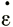_х - скорость продольной деформации на поверхности и В₁ - простое линейное осреднение параметра В и погрешность, вносимая интегралом уравнения (19). Теперь уравнение (16) приобретает вид

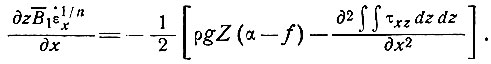
(22)

Шумский [122, 123] считал член в правой части уравнения (22), содержащий параметр τ_xz, пренебрежимо малым.

Для ламинарного течения 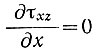и в общем случае зависит от изменений вертикальной скорости вдоль линии тока. Оценим роль этого члена уравнения (22) при течении ледника по волнообразному ложу. Если сила сцепления на поверхности равна нулю, то напряжение сдвига τ_xz на поверхности, скажем τ_п, связано с девиатором продольного напряжения и наклоном поверхности α_п соотношением

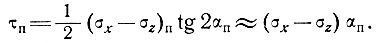
Теперь, если скорость продольной деформации незначительно изменяется с глубиной по всей массе льда, за исключением базисного слоя, можно принять следующее допущение для расчета изменения сдвигового напряжения с глубиной:

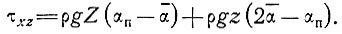
(23)

Здесь напряжение сдвига τ_xz равно ρg(α_п - α)Z на поверхности (α_п и 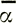- местные и региональные наклоны поверхности), которое изменяется линейно с глубиной до величины τ_осн = ρgαZ у основания. Эту величину мы принимаем постоянной по оси х.¹

¹(Другие допущения, помимо 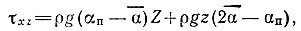, такие, как τ_xz = ρg(α_п-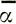)z или τ_xz = ρg(α_п-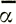)Z, приводят к аналогичным результатам, но коэффициент р, равный в уравнении (29) 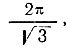, в данном случае составляет соответственно )

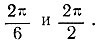Пользуясь выражением (23), находим

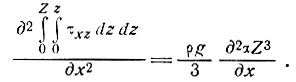
(24)

Теперь рассмотрим, как отношение 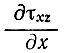влияет на изменение деформации сначала на волнах поверхности на сравнительно небольших расстояниях х, где Z = const, а затем на больших протяжениях массы льда, где учитывается общая кривизна льда.

Волнообразная поверхность куполовых ледников. Рассмотрим короткий участок куполового ледника с небольшими флуктуациями длиной волны ??? по высоте по сравнению с толщиной льда Z.

Высоту ледника Н можно выразить следующим образом:

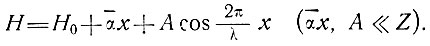
(25)

Наклон поверхности ледника тогда составит

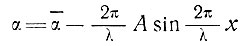
(26)

Пользуясь выражением (24) и предполагая, что Z и В остаются постоянными на всем участке, можно уравнение (22) приближенно записать в виде:

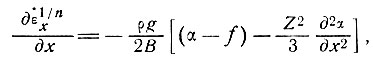
(28)

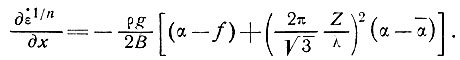
(29)

Поскольку 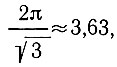находим, что для волн поверхности с небольшим периодом колебаний (λ ≈ 3,63 или меньше) второй член уравнения (28) ∂²/∂х² становится существенным. Если f = 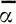(как это следует из данных, полученных на ст. Уилкс, см. раздел 6), то влияние второй производной наклона поверхности ледника для волн с небольшим периодом сводится к усилению относительного максимального растяжения на гребнях волн и относительного сжатия во впадинах.

Крупномасштабная кривизна куполового ледника. Чтобы оценить величину второго члена в правой части уравнения (22) в большом масштабе, приняв, что в идеальном случае α = f в уравнении (22), проинтегрируем и разделим это уравнение на 2В, и из уравнения (24) получим

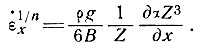
(30)

Рассматривая формы куполовых ледников вида Z = х^m npи m = 1, ¹/₂, ¹/₃,..., можно увидеть, что хотя скорости деформации и скорости движения, выведенные из уравнения (30), сопоставимы со скоростями, рассчитанными в разделе 6, с учетом допущения, что напряжение сдвига в базисном слое пропорционально наклону поверхности куполового ледника большого масштаба, эти величины оказываются весьма малыми.

Члены уравнения (30) будут исследованы ниже применительно к различным гипотетическим куполовым ледникам, после того как будет найдено выражение скорости движения масс льда на большом протяжении ледника. Здесь достаточно констатировать, что в масштабе, примерно в 10 - 20 раз большем, чем толщина льда, этой величиной можно пренебречь, но для волн с небольшим периодом колебаний (λ≈3,6) она становится существенной и рассматривается с учетом особенностей течения льда по волнообразному ложу (см. подраздел 5.4).

Запишем основное уравнение скорости продольной деформации в виде

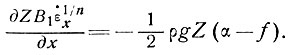
(31)

В уравнении (31) предполагается, что флуктуации наклона, которые на небольших расстояниях, где Z, f и В можно считать константами, вызывают соответствующие флуктуации скорости продольной деформации, т. е.

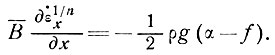
(31а)

Отсюда вытекает способ определения f - путем измерения мелкомасштабных изменений деформаций и наклона поверхности ледника. Если чистая скорость деформации на больших расстояниях очень мала или относительно постоянна, то из уравнения (31), если

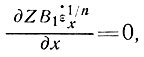
найдем, что f→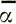. Это означает, что на больших расстояниях при сглаженных значениях параметров формула базисного напряжения, полученная Наем:

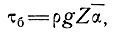
(32)

является приемлемым приближением. Фактическое расстояние, на котором происходит сглаживание, дано в п. 5.4.3.

По уравнению (31) можно определить значения n и В, сравнив изменения напряжения, обусловленные изменением наклона, с результирующими изменениями скорости деформации, т. е. по уравнению

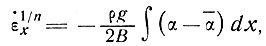
(33)

где интеграл берется по полуволне. Значение этого уравнения подробно рассматривается в разделе 6.

Рассмотрим далее профиль продольной скорости, который при больших масштабах определяется в основном кривизной ледникового купола, а не небольшими флуктуациями наклона. Для этого определим сначала связь скорости на поверхности с базисным сдвиговым напряжением. Най [87, 89, 90] показал, что наличие небольшой скорости продольной деформации не оказывает значительного влияния на вертикальный профиль скорости.

Мы можем выразить 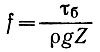в значениях скорости на поверхности. Принимая τ_xz = ρg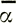z и закон течения

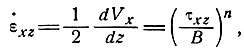
(34)

получим

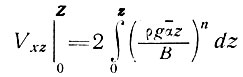
(35)

или

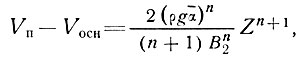
(36)

где V_п, V_осн - скорости на поверхности и у основания соответственно, В₂ - среднее взвешенное значение, полученное в результате интегрирования и зависящее от температурного распределения, определяется как

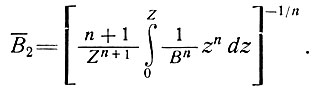
(37)

Параметр B₂ есть по существу осредненное значение параметра В в базисных слоях. При изотермических условиях 94% величины интеграла для В определяется нижней половиной массы льда. (Более того, типичный положительный температурный градиент (≈ 2÷4°С/100 м) у основания дает еще меньшие величины В. Это приводит к тому, что В₂ фактически определяется температурой в самых нижних 10 - 20% льда. Поэтому для этих значений В и n будет принят индекс 2, чтобы отличить их от значений В и n уравнения (31), которые характерны для среднего значения по, колонке. По уравнениям (36) и (23) для напряжения в базисном слое можно записать

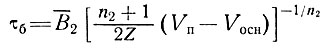
(38)

Для холодной массы льда (температура в базисном слое существенно ниже нуля) можно ожидать, что V_осн = 0. Отсюда с учетом выражений (33) и (11) уравнение (22) может быть записано в виде

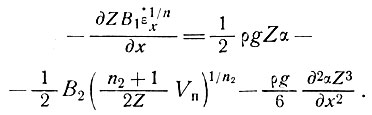
(39)

Это - дифференциальное уравнение второго порядка для скорости, содержащее параметры течения и граничные размеры массы льда, т. е. толщины льда и наклона поверхности. При точном знании параметров течения можно было бы использовать уравнение (39) для расчета скорости деформации вдоль движения ледника при условии, что известны граничные величины скоростей движения и деформации в некоторой граничной точке. С другой стороны, если скорости деформации и движения могут быть измерены по всей толщине ледника, то можно рассчитать эффективные параметры течения.

Так как степенной закон течения справедлив лишь для небольшого диапазона напряжений, то величины n и В в левой и правой частях уравнения (39) могут быть совершенно неидентичными, поскольку они относятся к совершенно различным частям ледника с разными напряжениями и температурами. Значения этих величин в левой части уравнения связаны с продольной деформацией пр всей глубине ледника, в то время как в правой части они относятся к большому сдвигу в базисных слоях. В частных случаях, где имеют место равенства

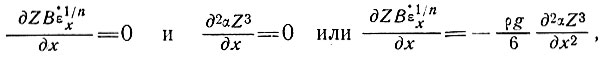
получим f = 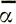, что приводит к следующему уравнению для продольной скорости:

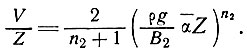
(40)

Это уравнение эквивалентно результату, который получил Хефели, для случая, когда В - константа, и которым он воспользовался для определения скорости вдоль линии тока массы льда в Гренландии [40, уравнение (12)].

Можно ожидать, что эта зависимость скорости от толщины льда, наклона поверхности и параметров закона течения будет справедлива для их сглаженных значений при больших масштабах при условии, что средняя скорость продольной деформации мала, в отличие от мелкомасштабных флуктуаций наклона и скоростей деформации, описываемых уравнением (33). Поскольку параметр В зависит от температуры, необходимо знать также и распределение температур по всей массе льда.

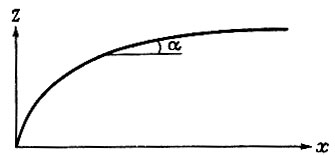
Кривизна куполового ледника

Рассмотрим теперь зависимость параметра τ_zx от кривизны куполового ледника:

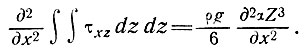
Пусть профиль куполового ледника определяется зависимостью

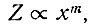
(41)

где Z - толщина льда на расстоянии х в глубь континента от края ледника.

Если предположить, что ложе горизонтально, то имеем

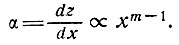
Тогда уравнение (30) даст нам для скорости деформации соотношение

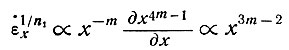
(42)

при условии, что В = const.

С другой стороны, если уравнение (40) справедливо, получим

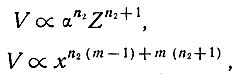
следовательно,

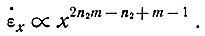
(43)

Приравнивая эти выражения, получим равенства экспонент, т. е.

(44)

или

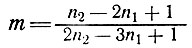
(45)

при n = 1 m = ¹/₂ для всех значений n₂, при n₁ = 2 и n₂ = 3 m = 0, при n₁ = 2 и n₂ = 3,5 m = ¹/₄, при n₁ = 2 и n₂ = 4 m = ¹/₃. Также, если n₂→∞ m → ¹/₂.

Най [84, 85] установил, что парабола Z = x¹/₂ эквивалентна зависимости τ_б = ρgαZ для пластического твердого тела. При высоких значениях n2 мы также приближаемся к этой зависимости, поскольку формы многих существующих куполовых ледников (см. раздел 7) приближенно описываются этой зависимостью. Для рассчитанных выше больших значений 1/m, как можно видеть, требуются лишь небольшие различия в значениях n₁ и n₂, чтобы сохранялось соответствие между отношениями

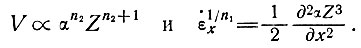
Реальные значения этих параметров будут рассмотрены в разделе 6.

Хотя изменения наклона ложа и параметра В приводят к необходимости модификации этого общего расчета, представляется, однако, что наличие члена 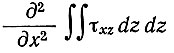в уравнении (22) не противоречит использованию уравнений продольной скорости (40) и скорости деформации (33) для определения параметров течения. В разделе 6 будет показано, что это справедливо.

Результаты этого двухмерного анализа применимы и к ледниковым щитам, где скорости поперечной деформации пренебрежимо малы. В подразделе 5.2 этот метод будет распространен на некоторые простые трехмерные модели, чтобы охватить случаи глетчеров, где поперечный сдвиг играет существенную роль. Это будет сделано введением величин, осредненных по поперечному сечению, и соответствующих коэффициентов формы [92, 93]. Поперечные растяжение и сжатие будут обсуждены в подразделе 5.3.