
4.6. Влияние аккумуляции и вертикального движения льда на профиль температуры масс льда
Эта проблема была подробно рассмотрена сначала Робином [115] и позднее Зотиковым [153], причем оба они выполнили весьма полезные теоретические расчеты профилей температуры и температурного градиента. Енсен и Радок [47, 48] получили численные решения, соответствующие конкретным случаям и учитывающие толщину льда, наклон поверхности, вертикальное и горизонтальное движение льда и скорость аккумуляции.
Результаты измерения температурных градиентов в Антарктиде [6, 14, 16, 17, 25, 37, 38, 77] показывают, что физические допущения принятые в теоретических расчетах, представляются, по крайней мере, частично справедливыми. Однако на данном этапе не существует подробных рядов температурных градиентов на поверхности ледников при их движении от побережья в глубь континента в районах, где остальные параметры движения льда известны. Значения температурного градиента, полученные Баддом [16, 17] на леднике Уилкса, близки к температурным градиентам вдоль линии его движения, полученным Маклареном [71], и позволяют достаточно точно оценить скорости движения, характерные для этого ледника. Однако эти скорости малы и, хотя они вполне сопоставимы со скоростями, полученными при анализе имеющихся в этом районе температурных градиентов, они не обеспечивают полной проверки теории.
В этом и следующем разделах профили температуры в движущихся массах льда при наличии аккумуляции будут рассмотрены на примерах, представляющих самые простые ситуации, типичные для регионов Антарктиды. Основным достижением настоящей работы по сравнению с предшествующей является отказ от допущения существования установившихся профилей температур куполовых ледников. Изменение толщины ледников во времени может быть более важным, чем другие факторы, определяющие условия установившегося состояния. Например, этим могут объясняться положительные температурные градиенты, измеренные Батти [6] в толстом льду в Антарктиде. Более того, установлено, что изучение профилей температуры проливает новый свет на состояние равновесия масс ледников.
Высокие отрицательные температурные градиенты, измеренные на различных участках материка в верхних 50 метрах льда [115], были частично объяснены климатическими изменениями, происшедшими в последнее время. Климатические изменения вообще имеют довольно большую географическую протяженность, однако это не объясняет различных скоростей нагревания льда в соседних районах за один и тот же период времени. Здесь будет показано, что флуктуации топографии и наклона поверхности на небольших расстояниях (см. раздел 6) на поверхности некоторой массы льда связаны также с флуктуациями скорости деформации и аккумуляции. В результате этого на поверхности массы льда могут иметь место различные скорости нагревания на небольших расстояниях (≈5 ÷10 км), которые могут сохраняться в течение небольших периодов времени (примерно 1000 лет) и вызывать различные температурные градиенты в приповерхностных слоях льда по сравнению с более глубокими слоями. Эти флуктуации могли бы совершенно не зависеть от климатических изменений, и, таким образом, прежде, чем делать вывод о влиянии климатических изменений, следует сначала полностью проследить влияние движения масс льда на температуры в них.
Для начала рассмотрим простую модель, не учитывающую аккумуляцию или горизонтальное движение льда.
1. Для массы льда постоянной толщины Я, постоянной температуры θ и постоянного градиента температуры базисного слоя γб (соответствующих геотермическому тепловому потоку) при температурном градиенте на глубине z имеем
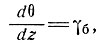
и, следовательно,
θz = θп-γбz.
Таким образом, температура льда у основания
θосн = θп-γбН,
(40)
т. е. температурный профиль просто определяется температурой поверхности θп и геотермическим градиентом базисного слоя γб (рис. 4.7). Подобная ситуация должна встречаться, когда чистая скорость аккумуляции близка нулю, а горизонтальная скорость движения льда мала. Поскольку геотермический поток очень важен при определении профиля температуры, необходимо знать, как он изменяется от места к месту. Ли и Иеда [61] суммируют все имевшиеся к 1964 г. по этому вопросу данные. Исходя из результатов их работ, следует отметить, что по Гренландии и Антарктиде данных по существу нет. Однако Ли и Иеда установили высокую степень корреляции между тепловым потоком и основными геологическими особенностями земной поверхности:
| - | Среднее и стандартное отклонение μ кал/(см2·с) |
| На суше | - |
| Докембрийские щиты. . . . . . . . . . . . . . . . . . . . . . . . . . . | 0,92±0,17 |
| Палеозойские орогенезисные районы. . . . . . . . . . . . . | 1,23±0,4 |
| Последокембрийские неорогенезисные районы. . . . | 1,54±0,38 |
| Мезозойско-кайнозойские орогенезисные районы. . . | 1,92±0,49 |
| На море | - |
| Океанские впадины. . . . . . . . . . . . . . . . . . . . . . . . . . . . | 0,99±0,61 |
| Океанские бассейны. . . . . . . . . . . . . . . . . . . . . . . . . . . . | 1,28±0,53 |
| Океанские хребты. . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 1,82±1,56 |
Эта корреляция теплового потока с основными геологическими особенностями предполагает, что тепловой поток в Гренландии и Восточной Антарктиде составляет величину, близкую к 0,9μ кал/(см2·с), что типично для старых докембрийских щитов, в то время как Западная Антарктида с ее более поздним происхождением может иметь более высокий геотермический поток. Отметим, что если θосн→0, то поправка, приведенная в пункте 4.4.1, будет справедливой.
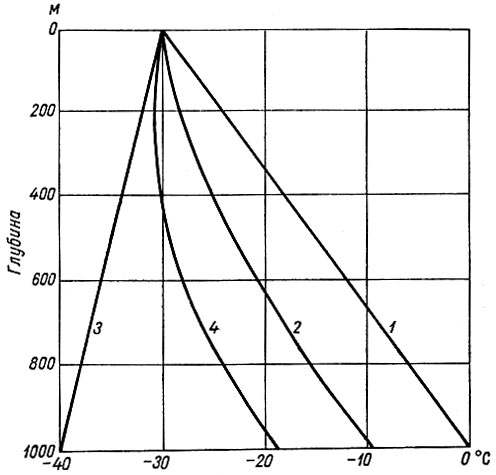
Рис. 4.7. Зависимость температуры льда от его толщины для куполового ледника толщиной 1000 м, определенная по значениям: 1 - θп и γб (нулевое накопление) ; 2 - θп, γб и А (робиновское установившееся накопление); 3 - θп, А и нагревания поверхности αVλ, но без величин теплопроводности (робиновское нагревание поверхности); 4 - θп, γб, А и αVλ
2. Для второго случая пока еще нет данных о горизонтальном движении, однако мы вводим скорость аккумуляции А на поверхности. Делается допущение, что толщина льда постоянна во времени, а скорость продольной деформации постоянна по глубине, так что вертикальное движение на уровне z выше основания определяется выражением
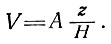
Это модель установившегося состояния Робина [115], для которой он нашел следующее решение:
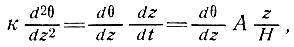
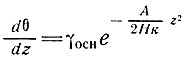
(41)
и
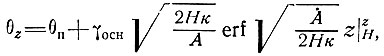
(42)
где
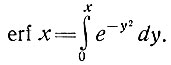
В частности, температурный градиент на поверхности выражается как
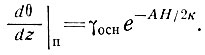
(44)
Можно полагать, что это решение близко соответствует действительности в районах малого горизонтального движения (таких, как на вершине купола или ледоразделе) и если сохраняется установившееся состояние и не происходит климатических температурных изменений.
Отметим, что, поскольку 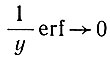 при у→0, уравнение (42) сводится к нашим результатам, полученным для модели 1, когда скорость аккумуляции становится небольшой.
при у→0, уравнение (42) сводится к нашим результатам, полученным для модели 1, когда скорость аккумуляции становится небольшой.
Чтобы проанализировать некоторые типичные значения поверхностного температурного градиента по Атарктиде, рассмотрим табл. 4.3 и 4.4 и рис. 4.8 и 4.9.
Таблица 4.3
Температурные градиенты установившегося состояния γоснe-АН/2к, по Робину
| АН/2к. . . . . . | 0,1 | 0,5 | 1 | 2 | 3 | 4 | 5 | 6 |
| exp АН/2к. . . | 1,1 | 1,65 | 2,72 | 7,4 | 20 | 54 | 150 | 400 |
| γп °С/100 м. . | - | - | - | - | - | - | - | - |
| γосн = 2,2. . . . | 2,0 | 1,3 | 0,81 | 0,30 | 0,11 | 0,04 | 0,015 | 0,005 |
| γп = 4,4. . . . . | 4,0 | 2,6 | 1,6 | 0,60 | 0,22 | 0,081 | 0,030 | 0,01 |
На большей части территории Антарктиды градиент температуры поверхности, соответствующий модели установившегося состояния Робина, менее 1°С/100 м. Можно ожидать, что на большей части континентальной области этот градиент будет менее 0,1°С/100 м.
Таблица 4.4
Значения параметра АН/2к
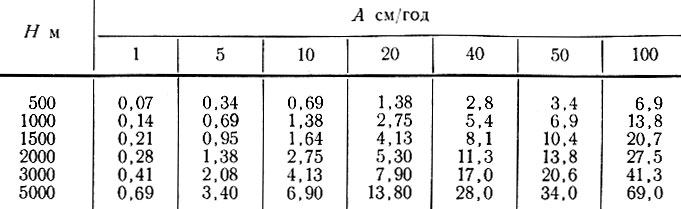
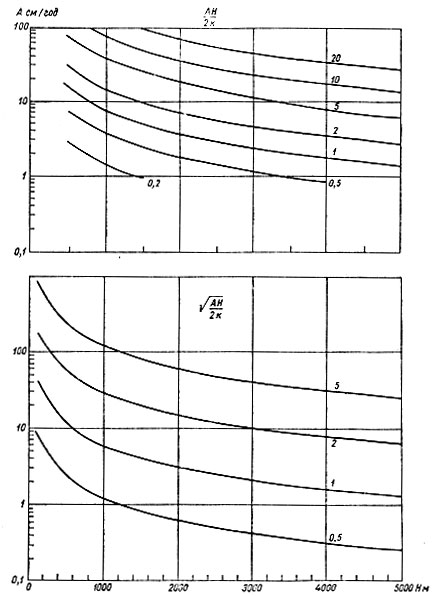
Рис. 4.8. Безразмерные величины АН/2/к и АН/2к для типичных значений А и Н и постоянного k≈1,16×10 см/с
Значения температурного градиента, рассчитанного по уравнению (44) вдоль линии ст. Уилкс - ст. Восток по данным Батти [6] и Уолкера [138], приведены в табл. 4.5. Ясно, что температурный градиент, рассчитанный по формуле Робина для установившегося состояния, пренебрежимо мал вдоль почти всей рассматриваемой линии в противоположность измеренным температурным градиентам, которые к тому же в большинстве своем отрицательны. Даже для глубинных районов континента, где измеренные температурные градиенты положительны, представляется, что расчетных градиентов для данной модели пока еще слишком мало, чтобы объяснить результаты измерений.
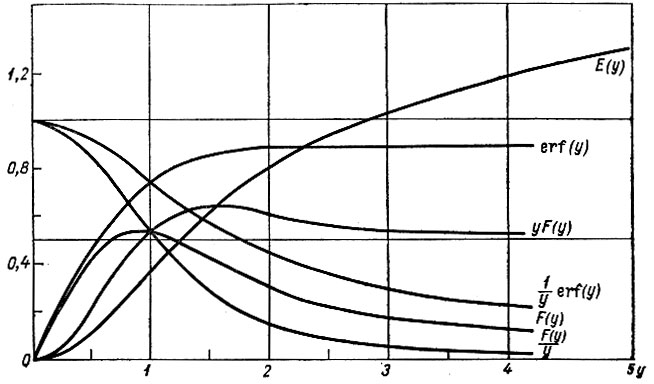
Рис. 4.9. Функция погрешности erf у, интеграл Доусона F(y) и его интеграл F(у) для величин аргумента в диапазоне типичных значений
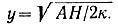
Таблица 4.5
Температурные данные вдоль линии ст. Уилкс - ст. Восток
| x, км. . . . . . . . . . . . . | 178 | 280 | 370 | 463 | 516 | 570 | 720 | 820 | 920 | 1020 | 1120 | 1206 | 1312 |
| h, м. . . . . . . . . . . . . . | 855 | 1475 | 2115 | 2515 | 2650 | 2740 | 2910 | 3015 | 3180 | 3280 | 3380 | 3530 | 3640 |
| Н, м. . . . . . . . . . . . . . | 3200 | 2055 | 2500 | 2890 | 2690 | 3700 | 4600 | 4560 | 4320 | 3380 | 3460 | 2890 | 3140 |
| θп°С на глубине 15 м | -19,0 | -27,0 | -32,5 | -37,8 | -40,4 | -43,6 | -52,7 | -54,8 | -57,2 | -57,5 | -59,3 | -59,6 | -60,4 |
| А, см2/год. . . . . . . . . | 35,0 | 35,0 | 17,0 | 5,2 | 12,0 | 9,1 | 10,5 | 8,8 | 8,8 | 5,2 | 10,5 | 7,0 | 5,2 |
| γп, °С/100 м. . . . . . . | -0,2 | 1,9 | -1,7 | -1,1 | -1,2 | -0,7 | 0,4 | -0,7 | 0,3 | -0,2 | 1,1 | 0,6 | 0,6 |
| γR °C/100 м. . . . . . . . | 10-5 | 10-4 | 10-4 | 0,17 | 0,01 | 0,1 | 10-4 | 10-3 | 10-3 | 0,4 | 10-3 | 0,07 | 0,17 |
|
ПОИСК:
|
© GEOMAN.RU, 2001-2021
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'