4.7. Влияние горизонтального и вертикального движения льда на профиль температуры ледника

Робин [115] первым рассмотрел совокупное влияние горизонтального движения и аккумуляции на профили температуры в ледниковых куполах. Прежде всего, если пренебречь теплопроводностью (для высоких скоростей движения и аккумуляции), отрицательный температурный градиент на поверхности 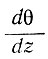определяется по формуле

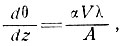
(45)

где V - скорость движения вниз по склону с углом наклона α (небольшим) при вертикальном градиенте температуры воздуха λ ≈ 1 °С/100 м в прибрежных районах Антарктики и скорости аккумуляции А.

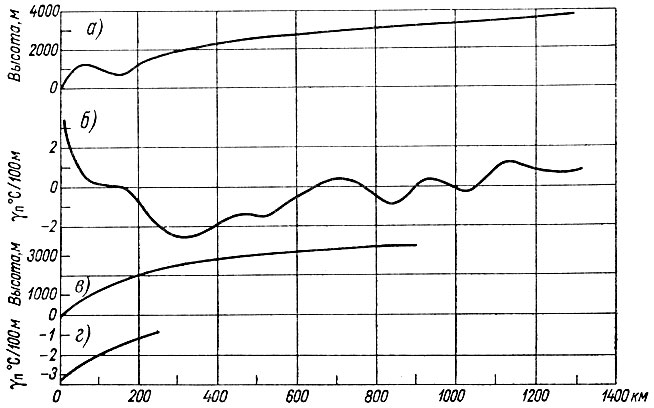
Рис. 4.10. Измеренные поверхностные градиенты температуры в Восточной Антарктиде. Профиль высоты (а) и поверхностные температурные градиенты (б) вдоль линии ст. Уилкс - ст. Восток; профиль высоты (в) и поверхностные температурные градиенты (г) вдоль линии ст. Восток - ст. Мирный

Радок [108] указал, что температурный градиент на поверхности также асимптотически приближается к 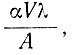, когда t→ ∞, при теплопроводности в полубесконечной среде, аккумулирующей на поверхности со скоростью А и постоянно нагревающейся со скоростью αVλ, независимо от теплопроводности.

Рис. 4.11а. Изменение физических параметров льда в глубь материка от станции Уилкс, измеренных (Н, α, А, V, θ_п, γ_п) и рассчитанных (τ, V, γ_б, θ_б) по данным Уолкера [138] и Бэтти [6]

Отрицательные температурные градиенты, измеренные от станций Уилкс и Мирный в глубь континента [14], представлены на рис. 4.10. Величина этого градиента в обоих случаях уменьшается в направлении движения. При удалении от ст. Уилкс в глубь континента они даже становятся положительными (рис. 4.11). Типичные значения αV и 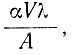приведены на рис. 4.12 и 4.13, что позволяет оценить величину влияния горизонтального движения льда на профиль температур в Антарктиде.

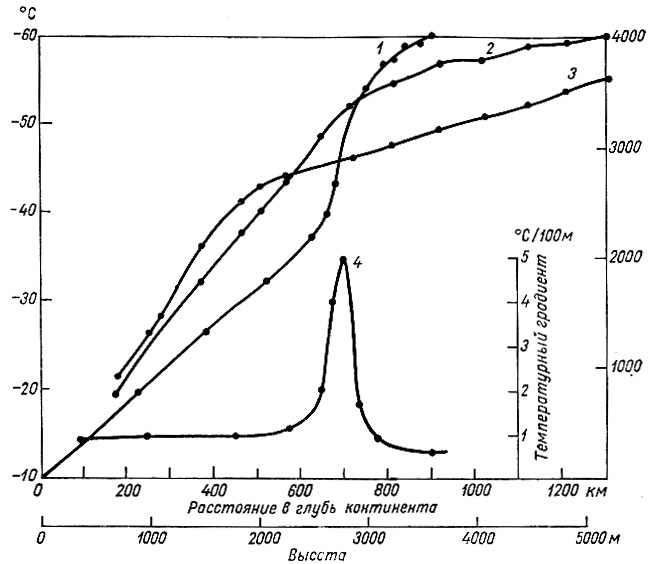
Рис. 4.11б. Температура и высота поверхности ледника в глубь континента от ст. Уилкс. 1 - зависимость температуры ледника от его высоты, 2 - температура ледника через каждые 10 м, 3 -высота над ур. моря, 4 - температурный градиент

Если предположить скорость V для линии ст. Восток - ст. Уилкс такой, чтобы выводной сток массы льда компенсировался аккумуляцией, можно рассчитать соответствующие градиенты температуры, вызванные только этим влиянием.

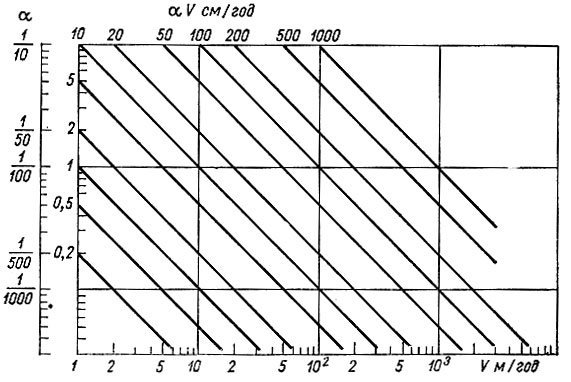
Рис. 4.12. Зависимость величин скорости установившегося понижения уровня ледникового купола αV от типичных величин скорости V и наклона поверхности а больших ледниковых масс

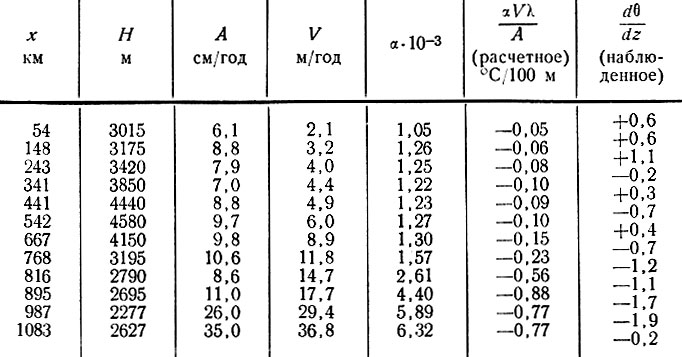
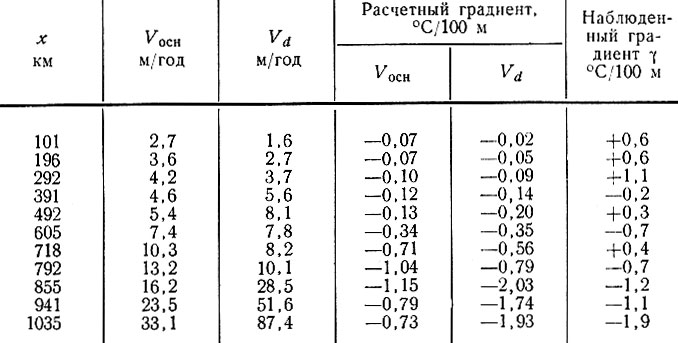
В табл. 4.6 видно близкое согласие между рассчитанными и измеренными градиентами для района побережья, где встречаются высокие отрицательные температурные градиенты. Расхождения могут быть следствием погрешностей расчета скоростей движения льда или влияния теплопроводности. Эта модель не объясняет положительных градиентов, наблюдающихся при движении в глубь континента.

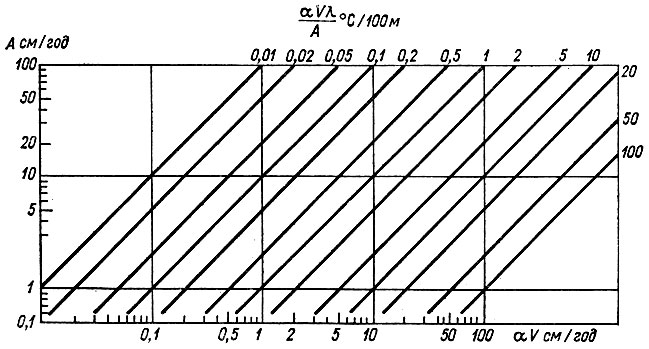
Рис. 4.13. Зависимость отрицательного градиента температуры на поверхности ледника от нагревания поверхности αV при аккумуляции А и нулевой теплопроводности

Таблица 4.6

Теперь рассмотрим влияние движения льда по склону на профиль температуры при наличии теплопроводности, но без аккумуляции. Здесь движение предполагается таким медленным, что оказывается возможным установившееся состояние, т. е. профиль температуры льда постоянен во времени в данной точке ложа. По мере того как лед движется по склону, он нагревается с той же скоростью, что и его поверхность.

В этом случае для изменения температуры "колонки" льда во времени, движущейся вместе с ледником, имеем

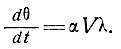
(46)

Следовательно,

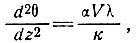
(47)

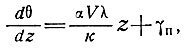
(48)

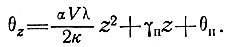
(49)

Поверхностный температурный градиент может быть выражен в значениях температурного градиента базисного слоя следующим образом:

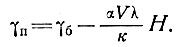
(50)

Следовательно,

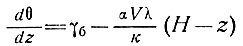
(51)

и

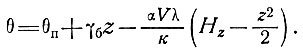
(52)

О характерных значениях температурного градиента, который мог бы возникнуть в результате влияния скорости горизонтального движения и аккумуляции в различных массах льда, можно судить по табл. 4.7 и 4.8. Таблица 4.8 и рис. 4.13 для безразмерного параметра αVH/к дают температурный градиент на поверхности в °С/100 м, при этом следует учесть, что λ (вертикальный градиент температуры воздуха) равен примерно 1°С/100 м.

Формула γ_п = αVλ/A предполагает, что температурный градиент на поверхности большой, когда скорость аккумуляции мала.

Таблица 4.7

Формула αVH/к показывает, что для среды конечной толщины поверхностный температурный градиент в установившемся состоянии имеет максимальный предел даже при нулевой аккумуляции.

Таблица 4.8

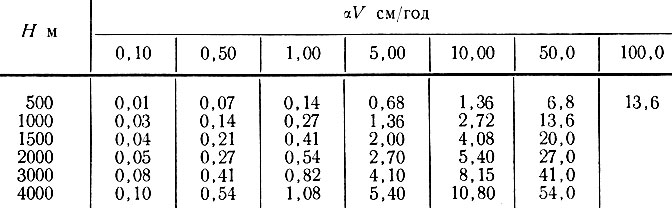
Сопоставляя таблицы (4.7 - 4.9) для безразмерных параметров αV/A и αVH/к и рис. 4.13, можно сравнить величины этих двух эффектов. Ясно, что в характерных для Антарктиды условиях они сопоставимы. Следующий этап - сравнение совместного влияния нагревания поверхности как при теплопроводности, так и аккумуляции для глыбы льда конечных размеров (рис. 4.14).

Таблица 4.9

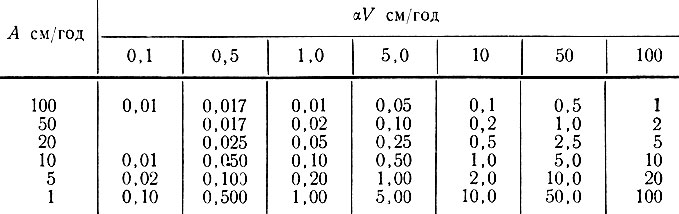
Включим в рассматриваемую модель влияние аккумуляции. Предполагается, что толщина льда Н остается постоянной при скорости аккумуляции на поверхности А и продольном растяжении, соответствующем вертикальной скорости аккумуляции А(Н - z)/Н на глубине г. Этот случай был рассмотрен Робином [115]. Для льда, медленно движущегося вниз по склону с углом наклона α, когда толщина льда остается постоянной и сохраняется профиль температуры при устойчивом состоянии, имеем дифференциальное уравнение, аналогичное уравнению (47), в виде

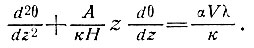
(53)

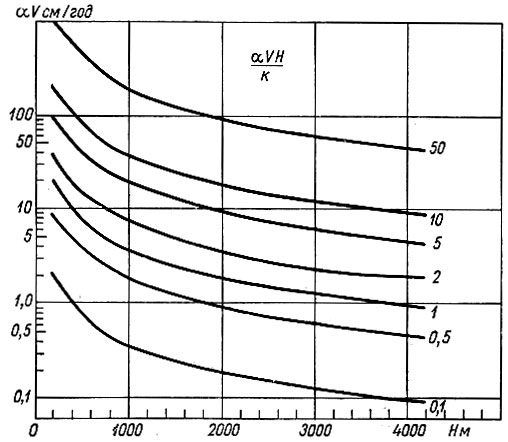
Рис. 4.14. Зависимость отрицательного градиента температуры на поверхности ледника от нагревания поверхности αV и теплопроводности при нулевой аккумуляции для различных толщин льда Н

Предполагается, что по мере течения льда рассматриваемая колонка от поверхности до основания нагревается с постоянной скоростью, а именно αVλ. Во многих случаях это допущение может быть весьма реалистичным, в других - более правильным было бы принять скорость нагревания в виде какой-либо другой функции от глубины, например, изменяющейся линейно от поверхности к основанию. Если бы температура у основания достигла точки таяния, скорость нагревания была бы равна нулю и уравнение, соответствующее выражению (53), имело бы вид

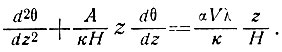
(53а)

Однако поскольку мы, в общем, не знаем, как нагреваются (или охлаждаются) нижние слои ледовых масс, рассмотрим сначала уравнение (53). После того как будет рассчитано несколько профилей температуры для установившегося состояния вдоль линии тока, вероятно, появится возможность заменить правую часть уравнения (53) более реалистичной функцией глубины.

Робин [115] нашел численные решения уравнения (53) для наблюдаемых профилей температуры и соответствующих им величин скорости V.

Найдем решение уравнения для температурного градиента следующим образом. Записав

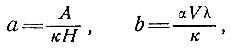
(54)

уравнение (53) приводим к виду

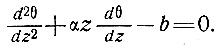
Это уравнение линейно относительно 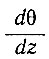при интегрирующем множителе е^+(а/2)z2.

Следовательно,

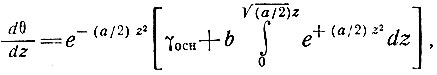
где γ_ocн - температурный градиент у основания ледника (z = 0). На поверхности (z = H)

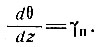
Отсюда

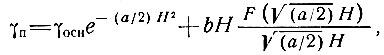
(55)

где F (x) - интеграл Даусона, определяемый как

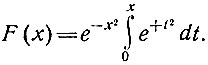
(56)

(Эта функция табулирована у Абрамовица и Стегуна [1].) Следовательно, температурный градиент на глубине z определяется выражением

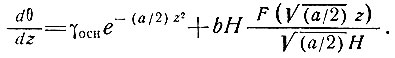
(57)

Заметим, что для данного случая ось z направлена вверх от основания и, таким образом, в уравнении (57) γ_осн - отрицательная величина.

В частности, температурный градиент на поверхности (z = H) становится равным

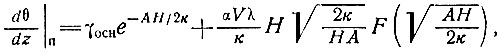
(58а)

что является обобщенным видом уравнения (50), или для сопоставления с формулой Робина [уравнение (45)] -

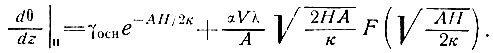
(58б)

Соответствующее решение уравнения (53а), в котором скорость нагревания уменьшается линейно до нуля у основания, будет иметь вид

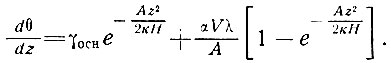
(57а)

Запишем уравнение (58)¹ в виде

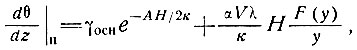
(58а')

¹(Формулы (58а) и (586) в силу их идентичности именуются в дальнейшем формулой (58).)

где 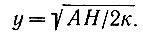. Теперь 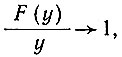когда у→0, и 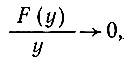становится большим. Таким образом, это решение сводится к предыдущему, т. е. к решению уравнения (50), когда А→0, а влияние аккумуляции заключается в простом уменьшении величин поверхностного температурного градиента.

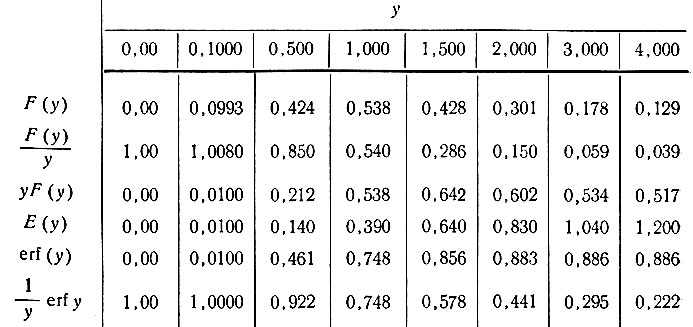
Типичные для внутренней Антарктиды величины 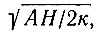, F(у), 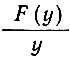представлены в табл. 4.10 и 4.12. Расчетные температурные градиенты для линии ст. Уилкс - ст. Восток даны в табл. 4.11. Эти градиенты удивительно близки к значениям, полученным расчетным путем (см. табл. 4.5) для случая, когда теплопроводностью пренебрегалось. Это является прежде всего следствием большой величины базразмерного параметра 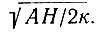. Поэтому уравнение (58) может быть записано в виде

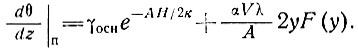
(58б')

Таблица 4.10

Кроме того, уF(у)→¹/₂, когда у∞→. Отсюда, когда Н→∞, А ≠ 0,

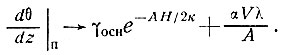
(59)

Таблица 4.11

Таким образом, приходим к выводу, что для мощной массы льда (Н большое), где скорость аккумуляции не слишком мала (А ≠ 0), температурный градиент на поверхности для установившегося состояния приближается к простой сумме результатов Робина [115]: 1) для установившейся аккумуляции и оседания без движения по склону и 2) для движения вниз по склону и аккумуляции в отсутствие теплопроводности.

Значения параметра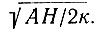

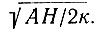
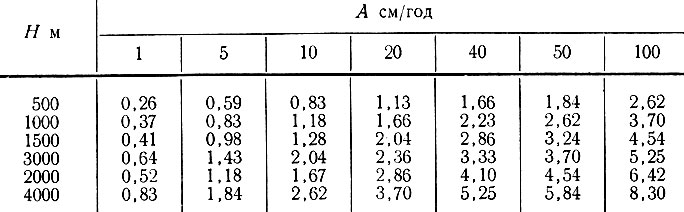
По данным табл. 4.10 видно, что при у>1 уF(у) не изменяется существенно (менее чем на 25%) от значения 0,5, а при у = 3 разница составляет менее 7%. По величинам 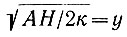в табл. 4.12 видно, что большинство антарктических куполовых ледников входит в категорию ледников с большим Н, т. е. 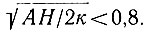. Поскольку значение выражения γ_осне^-АН/2к тоже мало для большей части континентальной Антарктики, получает объяснение близкое согласование между градиентами поверхностного нагревания Робина и градиентами, полученными по уравнению (58) для линии ст. Уилкс - ст. Восток.

Уравнение (58) позволяет сделать некоторые общие выводы относительно зависимости поверхностного температурного градиента от скорости аккумуляции и толщины льда.

Отрицательный температурный градиент, необходимый для поддержания установившегося состояния, возрастает по мере того, как вертикальная скорость αV по толщине Н увеличивается. Этот градиент становится более отрицательным по мере уменьшения температуропроводности (т. е. когда плотность в верхних слоях ледника понижается). Это соответствует увеличению аккумуляции (в сантиметрах). Уменьшение величины к оказывает аналогичное влияние на увеличение значения АН. По уравнению (58б) можно видеть, что в верхних слоях фирна, где температуропроводность мала, поверхностный температурный градиент более полно соответствует формуле Робина без теплопроводности 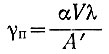, при условии, что А' принимается в качестве скорости аккумуляции фирна на соответствующей глубине. Эти результаты подтверждают справедливость использования формулы Робина (например, [16, 17, 77]) при установлении связи между поверхностными температурными градиентами и скоростями движения. Следует подчеркнуть, однако, что, за исключением установившихся ледниковых куполов, αV не является истинной вертикальной скоростью (см. подраздел 4.8), потому что, вообще говоря, она также включает в себя наклон основания и скорость вертикальной деформации, которые со временем могут привести к увеличению или уменьшению толщины куполового ледника.

Далее, интегрируя уравнение (57), получаем профиль температуры:

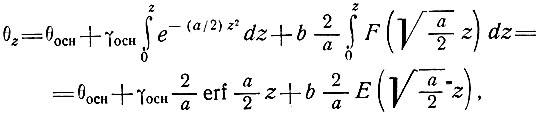
(60)

где Е(х) определяется из условия 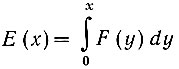и вычислено Зотиковым [153] для 0<x<3. Эту величину можно легко получить и по таблицам интеграла Даусона, составленным Абрамовицем и Стегуном [1]. График функции Е(х) для величин до х = 4 показан на рис. 4.10.

Температуру у основания находим по выражению

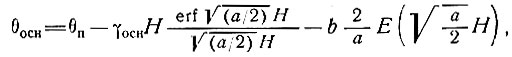
(61)

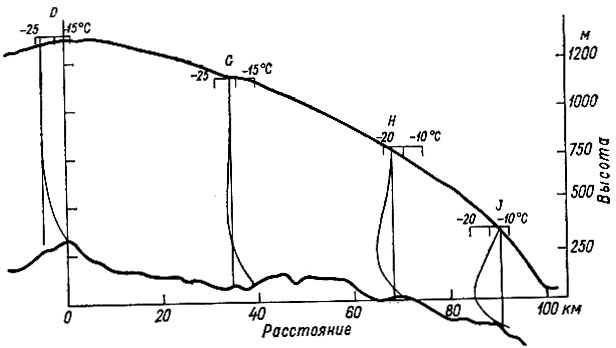
Рис. 4.15. Рассчитанные установившиеся профили температуры для части куполового ледника Уилкса

т. е.

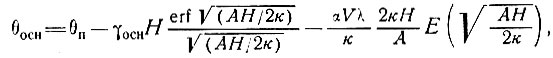
(61а)

или

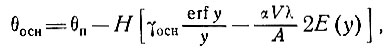
(62)

где градиент 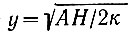- безразмерен (табл 4.12). Отсюда температурный профиль определяется как

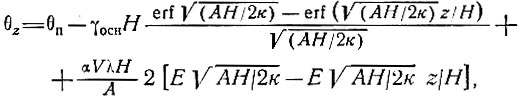
(60а)

или

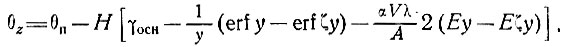
(63)

где ζ = z/H - часть толщины льда.

Типичные профили температуры для куполового ледника Уилкса показаны на рис. 4.15. Из этих профилей видно, что по мере приближения к побережью влияние возросшей скорости течения льда проявляется в увеличении отрицательного температурного градиента на поверхности и положительного у основания. Как следствие этого, средняя температура в массе льда ниже, чем температура его поверхности.

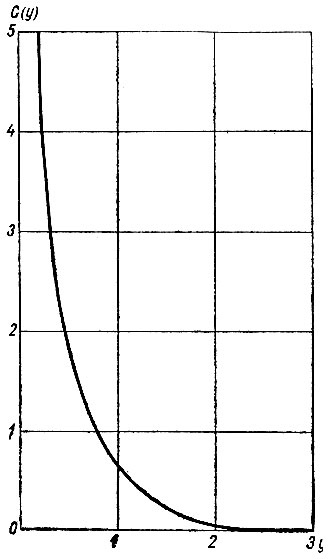
Рис. 4.16. Относительная глубина z/Н температурного минимума для установившихся распределений температуры во льду

Глубина нахождения минимума температуры определяется через dθ/dz = 0, что дает, согласно выражению (57),

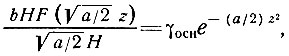
(64)

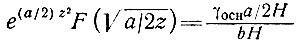
(65)

или, пользуясь уравнением (54),

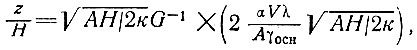
(66)

где 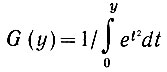(рис. 4.16).

Наконец, следует отметить, что дифференциальное уравнение (53) также может быть решено разложением в ряды по температуре и температурному градиенту. Эти ряды могут также быть получены из рядов для аналитических функций erf у, F(y) и других [1].