4.8. Профиль температуры растущего куполового ледника

Крэри [25] показал, что при медленном возрастании толщины Н шельфового ледника и постоянных остальных граничных условиях форма установившегося температурного профиля θ = f(H) оставалась той же при простой замене прежнего значения Я новым.

Для определения величины температуры θ на глубине z Крэри использовал дифференциальное уравнение

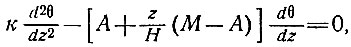
(67)

где к - температуропроводность, А - скорость аккумуляции на поверхности и М - скорость таяния льда у основания.

Из решения

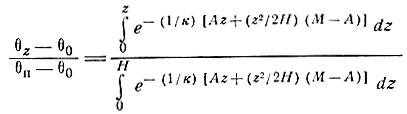
(68)

он получил численное выражение. Запишем

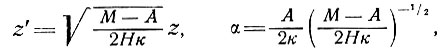
откуда

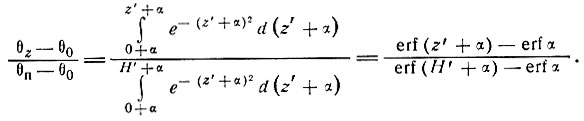
Обращаясь вновь к первоначальным параметрам [уравнение (67)], получаем

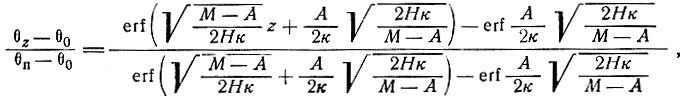
(69)

где θ_п - температура на поверхности и θ₀ - температура у основания. Этот результат предполагает, что решение для установившегося состояния при медленном увеличении или уменьшении толщины куполового ледника может быть найдено как функция нагревания или охлаждения поверхности при тех значениях вертикальной скорости и существующих физических параметров массы льда, которые характерны для данной точки.

Для массы льда с толщиной Н, высотой Е, скоростью аккумуляции А, наклоном поверхности α и наклоном базисного слоя β, которая движется с горизонтальной скоростью V и имеет скорость вертикальной деформации 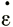_z, скорость изменения толщины льда над некоторой точкой ложа определяется уравнением

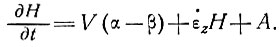
(70)

Вертикальная скорость на высоте z над ложем

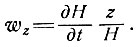
Теперь, пользуясь той же самой моделью, что и в подразделе 4.7, получаем дифференциальное уравнение для колонки, движущейся со средой, при условии, что координата z изменяется в зависимости от высоты Н, так что отношение z/Н остается постоянным:

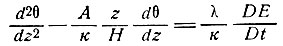
(71)

или

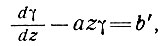
(72)

где

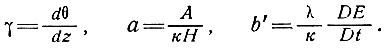
(73)

Нагревание поверхности выражается через повышение или понижение высоты поверхности Е куполового ледника в результате движения, т. е.

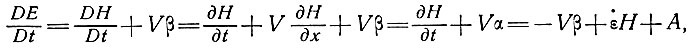
поскольку

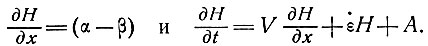
Для сбалансированного куполового ледника имеем ∂H/ ∂t = 0, и, следовательно, DE/Dt= Vα, то же, что и у Робина. Как и раньше (подраздел 4.7), дифференциальное уравнение (72) имеет решение

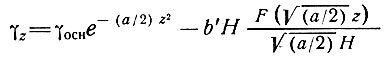
(74)

и, в частности, поверхностный градиент выражается следующим образом:

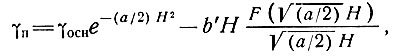
(75)

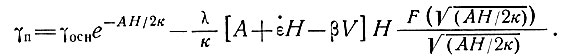
(75')

Отсюда можно видеть, что даже для очень толстого льда и высоких скоростей аккумуляции температурный градиент поверхности может быть положительным или отрицательным в зависимости от того, положительна или отрицательна величина DE/Dt, иначе говоря, для растущего ледникового купола температурный градиент поверхности становится положительной величиной, когда скорость аккумуляции увеличивается настолько, что выполняется условие

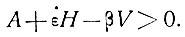
В 1963 г. Батти наблюдал положительные температурные градиенты поверхности в континентальной Антарктике. Поскольку робиновский член уравнения установившегося состояния е^-АН/2к мал, представляется, что причина в том, что поверхность ледникового купола поднимается. Мы можем рассчитать скорость роста величины ∂H/ ∂t, при которой имеет место положительный температурный градиент γ_п, по выражению (75):

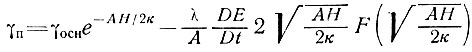
(75")

или, поскольку

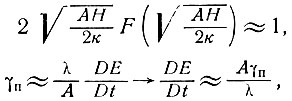
или

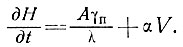
(76)

Типичные значения γ_п и λ, определенные вдоль линии ст. Уилкс - ст. Восток (см. рис. 4.11), дают основание предполагать, что подъем поверхности во внутренней области Антарктиды может составлять 20-25% скорости аккумуляции (т. е. ≈ 2,5 см/год), что является общим подтверждением положительного бюджета ледниковых масс в континентальной Антарктиде [5, 19, 32, 33]. Из этого вытекает ряд очень важных следствий.

Так, если нам известны климатические температурные изменения в течение некоторого периода, то из уравнения (76) можно определить скорость понижения поверхности. С другой стороны, если нам известна скорость понижения ледниковой поверхности, например, по измерениям дивергенции потока, то уравнение (76) будет служить нам своего рода путеводителем при определении происшедших недавно изменений температуры поверхности. Это означает, что температурный градиент поверхности может служить весьма эффективным средством для определения бюджета внутренних областей больших ледниковых масс. В качестве другого примера рассмотрим температурный градиент ледниковой поверхности (до глубины примерно 150 м) на Стасьон Сентраль в Гренландии [45, 79]. Здесь температурный градиент на глубине от 100 до 150 м составляет около 0,26°С/100 м, скорость аккумуляции - примерно 40 см/год (в пересчете на лед) и расчетная скорость движения льда и наклон [40] около 2 м/год и 0,002 соответственно.

Отсюда

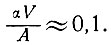
Из этого следует, что ожидаемый температурный градиент равен 0,1°С/100 м.

Это дает основание предполагать, что понижение поверхности (или чистый отрицательный бюджет ледниковых масс) составляет примерно 150% скорости аккумуляции, когда влияние климатических изменений пренебрежимо мало. С другой стороны, если бы это влияние было только следствием климатических изменений, то потребовалось бы повышение температуры воздуха примерно на 0,06°С/100 лет. Эта цифра не противоречит расчетным величинам недавних климатических изменений [30]. В расчетах, проведенных до сих пор, температуропроводность предполагалась постоянной. В действительности же теплопроводность льда, теплоемкость и температуропроводность, как оказывается, заметно зависят от температуры. Это показано в табл. 4.13 и на рис. 4.17.

Таблица 4.13

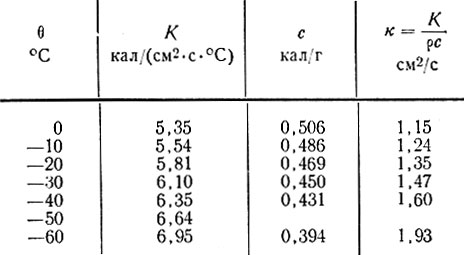
Учет температурной зависимости температуропроводности приводит к гораздо большей нелинейности уравнения теплопроводности. В этом случае существенное преимущество имеют численные методы. Здесь же мы просто введем среднюю величину температуропроводности для того конкретного температурного диапазона, который характерен для данного случая. При этом следует учитывать, что в зависимости от температурного диапазона погрешность в определении температуропроводности может достигать ±20%.

В задаче, которая до сих пор рассматривалась, имеется допущение об установившихся температурных условиях. Однако для очень толстого льда это установившееся состояние не может быть достигнуто. Временная зависимость, имеющая при этом место, значительно усложняет задачу. Самым удобным способом ее решения для любой конкретной ледниковой области является численный подход Енсена и Радока.

Если временная зависимость значительна, то недостаточно определить температурное распределение по величинам имеющихся параметров ледникового купола (скорость, аккумуляция, деформация и т. д.) в определенном месте, как это было сделано здесь. Надо в течение длительного времени проследить за движением и изменением ледникового купола по мере того, как лед движется от центра, накапливается, деформируется, увеличиваясь или уменьшаясь по толщине. Поскольку скорости и температуры во внутренней Антарктиде в значительной мере неизвестны, детальный расчет такого рода может на данном этапе быть не более чем умозрительным. С другой стороны, как только все параметры движения льда наряду с температурными распределениями станут известными, можно будет установить и его предысторию и, в частности, возможные изменения климата за последнее время (последние 100 000 лет).

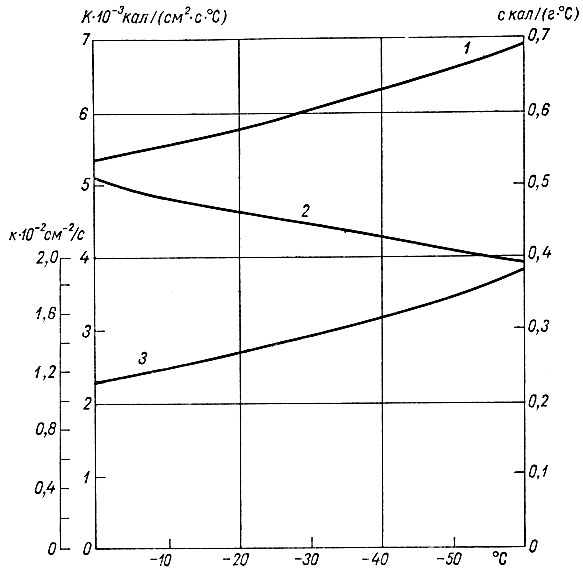
Рис. 4.17. Зависимость тепловых свойств льда от температуры. 1 - теплопроводность К, 2 - температуропроводность к, 3 - теплоемкость с