4.9. Справедливость предположения установившегося температурного распределения

Суть термина "установившийся" состоит в том, что параметр постоянен во времени. Это может быть температура, температурный градиент или толщина льда. В связи с этим мы даем следующие определения.

1. Мы определяем "установившийся температурный профиль" куполового ледника как такой профиль, который остается постоянным во времени и в пространстве над некоторой неподвижной точкой ложа по мере движения льда. В этом случае куполовый ледник должен находиться в установившемся состоянии.

2. Для динамичной поверхности куполового ледника мы можем определить "установившийся температурный профиль по толщине", если температура выражается постоянной функцией (во времени) толщины льда Я, даже если последняя медленно изменяется во времени.

3. Если вся колонка льда нагревается с постоянной скоростью (или, что более вероятно, со скоростью, которая является постоянной функцией глубины), то мы можем определить "профиль установившегося температурного градиента" как профиль, в котором температурный градиент остается постоянным во времени.

4. Подобно предыдущему, для растущей (или убывающей) колонки льда куполового ледника, которая нагревается со скоростью, являющейся постоянной функцией его относительной глубины, назовем "относительным профилем установившегося температурного градиента" такой профиль, температурный градиент которого представляет постоянную функцию толщины льда, способную изменяться во времени. Это более общий случай, рассмотрение которого необходимо для представления движущейся колонки.

Везде конечный результат - это выражение температуры или температурного градиента как функции от глубины, а не времени. Рассмотрим теперь, при каких условиях куполовый ледник может иметь профили температуры, соответствующие различным типам установившегося состояния. Чтобы сохранять установившийся температурный градиент по всей толщине льда, масса льда должна нагреваться с той же скоростью, с какой нагревается ее поверхность.

Поскольку по мере течения колонки льда в куполовом леднике от центра к периферии ее поверхность нагревается, возникает вопрос, нагревается ли и остальная часть колонки так, чтобы сохранять установившееся состояние, или же изменение температуры ее основания отстает от роста температуры поверхности. Время нагревания быстро уменьшается, когда скорость движения колонки и ее наклон возрастают по направлению к побережью. В этом случае, вероятно, профиль температуры не определяется установившимся состоянием, соответствующим постоянной скорости нагревания. Однако по мере приближения к побережью уменьшение толщины колонки и увеличение тепла, выделяющегося в результате трения при более высоких скоростях движения льда, способствуют реализации в массе льда установившегося состояния. Чтобы определить критерий, позволяющий судить об устойчивости установившихся температурных профилей в движущемся куполовом леднике, рассмотрим теперь зависящие от времени решения уравнения теплопроводности для глыбы льда конечных размеров и исследуем время, необходимое для достижения устойчивости.

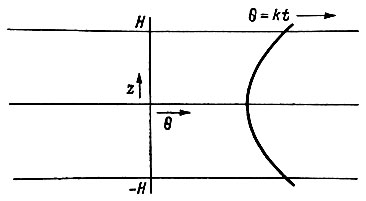
4.9.1. Куполовый ледник с постоянной скоростью нагревания поверхности. Рассмотрим, во-первых, простую модель - нагревание колонки льда при движении вниз и к периферии. Это имеет место для глыбы конечных размеров -H<z<H при нулевой аккумуляции и с постоянно повышающейся температурой поверхности. Такая задача рассмотрена Карсло и Ягером [22].

Принимаем для всей колонки начальную температуру равной нулю при t >0 и полагаем, что на поверхностях удерживается температура θ₀ = kt, где k = const. Температура θ на глубине z во время t определяется по выражению

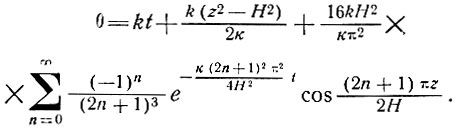
(77)

Формулу (77) можно использовать для имитации распределения температуры в колонке льда постоянной толщины Н до ложа, т. е. при z = 0. Температурный градиент в базисном слое в этом случае равен нулю; для куполового ледника, имеющего постоянный поток тепла в базисном слое γ_б, нужно просто к приведенному выше решению добавить член γ_бz.

Колонка льда

Согласно результатам, приведенным в подразделе 4.7, первый и второй члены в этой формуле являются решениями для установившегося состояния. Этот ряд представляет собой зависящую от времени часть уравнения, которая стремится к нулю при t→∞, и сходится очень быстро с возрастанием n, что свидетельствует о быстром демпфировании высокочастотных изменений. При n = 0 имеем

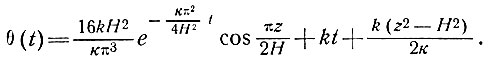
(77')

Можно видеть, что температура у основания (z = 0) стабилизируется в течение наибольшего промежутка времени.

Для температуры у основания имеем:

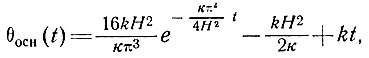
(78)

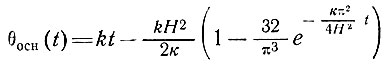
(79)

(заметим, ).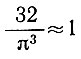

Рассмотрим теперь величину, стоящую под знаком экспоненты:

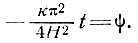
(80)

Чтобы величина температуры базисного слоя была в пределах 90% ее конечного значения, необходимо выполнение равенства t = 2,2 (4 Н²/кπ²).

При Н = 3000 м 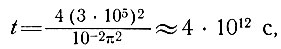или 1,3·10⁵ лет.

При Н = 1000 м 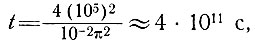или 1,3·10⁴ лет.

Следовательно, при постоянстве скорости нагревания куполового ледника в пределах полученных интервалов времени (для данной толщины льда) можно ожидать, что профиль температуры останется неизменным. Это будет в том случае, если скорость движения льда в континентальной Антарктиде равна приблизительно 1 м/год. Если скорость движения приближается к 10 м/год, то стационарное состояние не сохраняется.

Трудность состоит в том, что по мере удаления колонки льда от центра можно ожидать, что скорость ее нагревания возрастет. Поэтому рассмотрим изменение к во времени, приняв

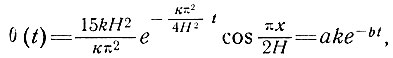
где

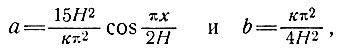
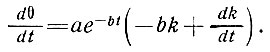
(81)

Для установившегося состояния величина отношения dk/dt должна быть малой по сравнению с величиной bk, или 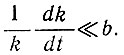. Если k = αVλ, то мы можем оценить величины 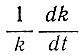в предположении постоянства λ из условия 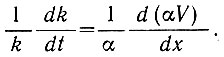. Типичные значения 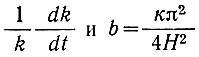, в год в год^-1 для различных толщин льда следующие:

Таким образом, величины 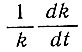сравнимы с величинами b или даже больше их. Это означает, что в отсутствие аккумуляции увеличение скорости нагревания льда по мере его удаления от центра ледника слишком велико, чтобы для столь толстого льда сохранялось установившееся состояние, соответствующее постоянной скорости нагревания.

Если стабильности в континентальной области Антарктиды не достигается, то различие во времени достижения установившегося температурного состояния в поверхностных и базисных слоях ледника может составлять примерно 30 000 лет. Это запаздывание может соответствовать пройденному расстоянию примерно в 100 км, и, следовательно, температуры у основания позволяют оценивать, в какой мере реализуются установившиеся состояния выше рассматриваемой точки.

Температурный градиент приближенно находится по формуле

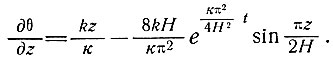
(82)

На поверхности (z = H) температурный градиент определяется как

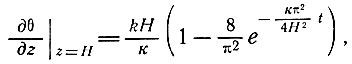
(83)

а у основания (z = 0) как

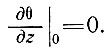
Можно ожидать, что для достижения устойчивости температурного градиента поверхности необходимо столько же времени, что и для температуры базисного слоя при постоянстве температурного градиента последнего. Величина температурного градиента на поверхности всегда меньше его предельной величины.

4.9.2. Масса льда с экспоненциально возрастающей скоростью нагревания. Поскольку в куполовых ледниках скорость нагревания поверхности непостоянна и быстро возрастает к побережью, то следует рассмотреть случай для массы льда толщиной - Н<z<Н, на поверхности которой температура изменяется во времени как Ve^νt, иначе говоря, нагрев поверхности происходит со скоростью νVe^νt = νT (где Т - температура в момент времени t). Эта задача была также рассмотрена Карсло и Ягером [22, стр. 105].

Для малых значений νe^νt ≈ 1 + νt и νе^νt ≈ ν. Поэтому для очень малых скоростей нагревания можно ожидать, что решение поставленной задачи приближается к нашему результату для постоянной скорости нагревания Vν = k и таким образом реализуются установившиеся профили температуры при постоянной скорости нагревания. Теперь определим величины ν, которые имеют достаточно малые значения. Решение этой задачи, полученное Карсло и Ягером, имеет вид

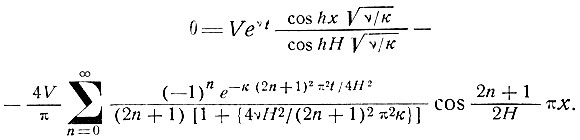
(84)

Асимптотическое решение для температуры у основания, если пренебречь членами, которые неограниченно убывают с течением времени, содержится в формуле:

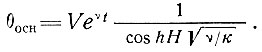
(85)

В предыдущем случае, т. е. когда нагревание постоянно и определяется величиной kt, мы имели

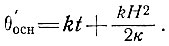
(86)

При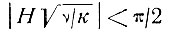

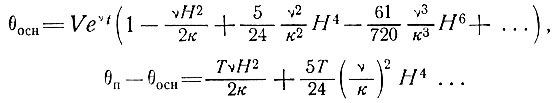
(87), (88)

Первый член в правой части уравнений соответствует ранее полученному результату при условии постоянной скорости нагревания к = νТ. Чтобы остальными членами можно было пренебречь, нужно

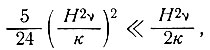
(89)

т. е.

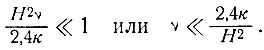
Для выяснения, как это условие реализуется на практике, введем в расчетные формулы величины, типичные для участков толстого и тонкого льда:

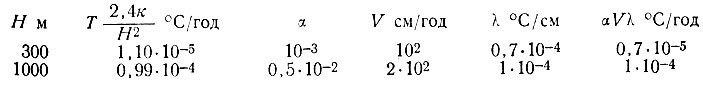
При этих значениях скорости движения и наклона поверхности скорости нагревания поверхности сравнимы по величине с 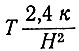и, следовательно, членами, имеющими в уравнении (88) более высокие степени, пренебречь нельзя. Отсюда следует, что скорости нагревания современных куполовых ледников с учетом их толщины слишком велики, чтобы сохранились устойчивые температуры масс льда в отсутствие аккумуляции и вертикальной скорости.

Влияние аккумуляции можно оценить по уравнению (71), если ввести в него члены, определяющие внутреннее нагревание льда, из уравнения (31), записанного в виде

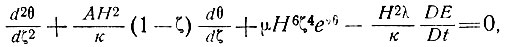
(91)

где

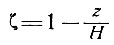
и

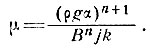
В качестве типичных можно принять А ≈ 10 см/год, 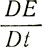≈ 10 см/год, μН⁶ ≈ 50, θ_п ≈ -30°С, λ = 1°С/100 м. Пользуясь этими величинами, находим, что для температуры поверхности первым и третьим членами уравнения (91) можно пренебречь, в то время как два других имеют значения примерно -30° С каждый. Около основания третий член достигает ≈ -50° С и становится доминирующим, но в других случаях им можно пренебречь.

Отсюда мы видим, что член уравнения (91), связанный с аккумуляцией на поверхности, имеет такую же величину, как и член, связанный с нагреванием, но противоположен последнему по знаку при отрицательных поверхностных градиентах (типичных для высоких скоростей нагревания) и, следовательно, уменьшает влияние нагревания. По мере возрастания глубины вертикальная скорость уменьшается, но то же происходит и с остающейся эффективной толщиной льда. Таким образом, в качестве приближенного критерия реализации установившегося состояния при наличии аккумуляции может быть принято условие (89), которое было выведено для случая, когда аккумуляция отсутствует:

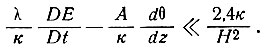
(92)

Для куполового ледника в установившемся состоянии

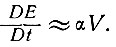
Согласно уравнению (58), температурный градиент на поверхности приближенно определяется выражением

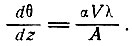
(93)

Отсюда неравенство (92) перепишем следующим образом:

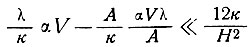
и его левая часть тождественно равна нулю.

Можно сделать вывод, что при достаточно высоких скоростях аккумуляции, обеспечивающих состояние массы льда, близкое к равновесному (в пределах 10%), влияние нагревания на поверхности компенсируется скоростью аккумуляции. Тогда чистое нагревание массы льда оказывается достаточно малым, чтобы эта масса сохраняла установившееся состояние при течении к побережью.