4.10. Проникновение поверхностных температурных изменений в аккумулирующую среду

Для больших периодов времени, для которых устанавливаются профили температуры, возникает вопрос, как длительные изменения температуры поверхности влияют на внутреннюю температуру массы льда. Зависимость внутренних температур накапливающегося снежного покрова от температурных изменений на поверхности массы льда рассматривалась Бенфилдом [8 - 10]. В то же время исследование периодических годичных синусоидальных температурных колебаний было проведено автором [16, 17]. Это исследование в принципе можно распространить на весьма большие периоды времени и, используя методы гармонического анализа, применить к другим формам температурных колебаний на поверхности.

Для случая нулевой скорости аккумуляции температурная волна на поверхности с амплитудой А₀ и частотой ω, определяемая как

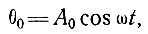
генерирует температурную волну на глубине z, т. е.

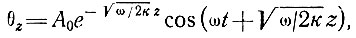
(94)

где к - температуропроводность льда.

Автор [16, 17] показал, что для аккумулирующей среды, т. е. среды, движущейся вниз от поверхности с постоянной скоростью u, амплитуда Az соответствующей температурной волны на глубине z связана с величиной А₀ зависимостью

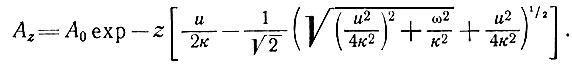
(95)

Отставание по фазе на глубине z определяется выражением

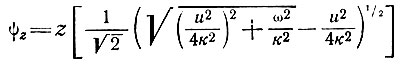
(96)

Скорость прохождения температурной волны в толщу льда при отсутствии накопления равна

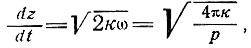
(97)

где р = 2π/ω - период волны.

Из формулы (95) следует, что при быстром накоплении массы льда или низкочастотных температурных изменениях, т. е. если 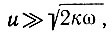, амплитуда температурной волны, проходящей сквозь среду, не уменьшается, а скорость этого прохождения равна вертикальной скорости движения льда. При медленном накоплении или высокочастотных изменениях температуры 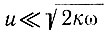температурная волна рассеивается как обычно в среде при отсутствии аккумуляции (табл. 4.14 и 4.15).

Таблица 4.14

В табл. 4.15 представлены параметры, характеризующие проникновение температурных волн с периодами от 1 до 10⁶ лет при отсутствии аккумуляции (т. е. скоростях накопления, значительно меньших, чем скорость проникновения).

Поскольку для температурных волн с периодом р<10³ лет скорость аккумуляции обычно пренебрежимо мала, то в табл. 4.15 дан точный прогноз глубин их проникновения в толщу массы льда. Эти с небольшими периодами колебаний волны очень быстро затухают в верхних нескольких сотнях метров и поэтому не могут оказывать влияния на температуру в глубоких слоях куполовых ледников. Только очень длинные волны проникают в глубокие слои. В табл. 4.16 показано время, требующееся для достижения волнами различных глубин во льду (от 100 до 4000 м), и уменьшение амплитуды температурных волн с различными периодами в отсутствие аккумуляции. Даже самые длинные температурные волны (10⁶ лет) существенно демпфируются на глубине в 4000 м, а на глубине 3000 м они лишь незначительно больше. Однако для этих длинных волн влияние аккумуляции является основным фактором.

Таблица 4.15

Время, требующееся для того, чтобы лед, отложившийся на поверхности, достиг глубины z, для массы льда, находящегося в состоянии равновесия, определяется уравнением

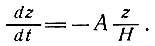
(98)

Средняя скорость установившегося движения льда равна А/2. Интегрируя уравнение (98), получаем

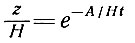
(99)

или

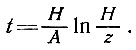
(100)

В частности, время, необходимое для достижения отложившимся льдом 90% глубины ниже поверхности, составляет

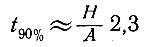
(табл. 4.17).

В действительности, для скоростей аккумуляции, равных 10 г/(см^-2 · год) или больших, температурные изменения с периодами 50 000 лет или более вследствие внутренней конвекции льда Доходят до основания ледника. За этот период при горизонтальной скорости от 1 до 5 м/год лед продвинулся бы на расстояние от 50 до 250 км. Для меньших скоростей аккумуляции можно сделать вывод, что ледовые массы толщиной 3000 - 4000 м в нижних слоях практически не подвергаются воздействию температурных флуктуаций с периодом менее чем 100 000 лет.

Таблица 4.16

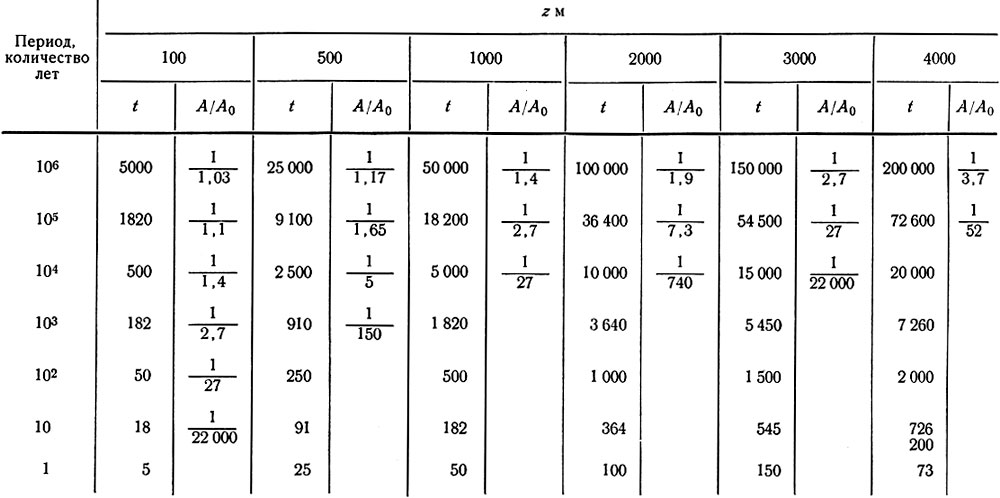
Примечание. t - время (количество лет), необходимое для достижения глубины z, А/А₀ - уменьшение амплитуды температурных колебаний.

Нагревание верхней поверхности льда по мере его течения к побережью можно рассматривать как изменения с очень большим периодом колебаний. Следовательно, в районах, где скорости аккумуляции достаточно высоки, температурная волна относительно быстро проходит через массу льда, а профиль температуры будет сохранять установившийся асимптотический характер, возможно, с небольшим запаздыванием по фазе у основания. Это запаздывание означало бы, что в зависимости от горизонтальной скорости температура основания соответствует температуре установившегося состояния льда на нескольких десятках километров вверх по его течению. Следует иметь также в виду, что в течение столь долгих периодов времени форма и размер ледникового купола могли претерпеть значительные изменения вследствие небольшого дебаланса в ледниковом бюджете. За 50 000 лет чистый дебаланс масс льда от 1 до 5 см/год привел бы к изменению толщины ледника от 500 до 2500 м. Этот подъем или опускание уровня льда может оказаться главным фактором, определяющим температурные изменения на поверхности ледников [см. формулу (100)].

Таблица 4.17

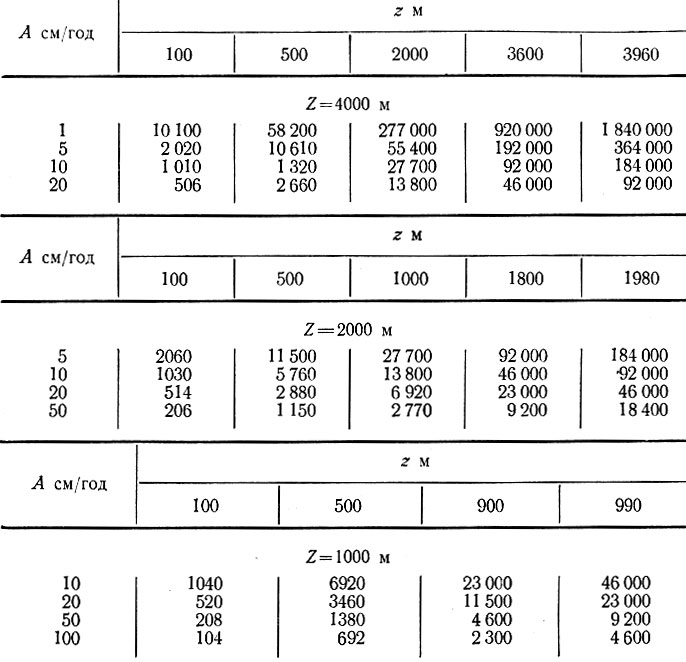
Подчеркнем еще раз, что оценка неустановившихся температурных градиентов очень сложна, так как необходимо ввести в расчет изменение граничных условий во времени и их текущие величины. Поэтому при определенной толщине, скорости аккумуляции, скорости движения, наклоне поверхности и основания, скорости деформации и т. п. нельзя дать какого-либо общего решения для температурного профиля в массе льда, т. е. решения в виде

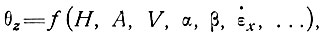
(101)

так как оно будет, кроме того, включать скорости изменения этих параметров за период времени, который требуется, чтобы лед переместился до занимаемого им в настоящее время положения. Другими словами, профиль температуры является функцией членов

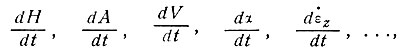
которые будут изменяться во времени и зависеть от координат. Это означает, что для интерпретации измеренного профиля температуры в некотором положении прежде всего должны быть получены все соответствующие данные, касающиеся движения, аккумуляции и т. п. в районе выше и ниже по течению масс льда вдоль линии их тока. Затем, если скорость течения и толщина льда достаточно малы для сохранения установившегося состояния, эти профили можно интерпретировать при помощи изложенной здесь в общих чертах теории. С другой стороны, если масса льда не находится в установившемся состоянии, можно использовать численный метод Енсена и Радока [48], чтобы проследить за движением колонки льда вдоль линии тока, интегрируя уравнение теплопроводности и учитывая действительные граничные условия в течение времени, достаточно длительного для того, чтобы в ледниковом куполе установилось присущее ему температурное распределение от некоторой предполагаемой величины. Если временные интервалы не слишком велики, то могут оказаться удобными методы теории возмущений, примененные к установившемуся профилю.

В плане эксперимента следует обратить внимание на получение профилей температуры для большого числа характерных точек (особенно вдоль линии тока), для которых имеются все требуемые данные. Важными характерными точками являются вершины куполов и ледоразделы, где горизонтальное движение пренебрежимо мало, а климатические изменения легко интерпретируются. Важность учета теплопотока у основания ледника в уравнениях для профиля температуры диктует необходимость получения сведений о температурном градиенте у основания и, желательно, непосредственно в самом ложе, т. е. в конечном итоге информации об изменениях геотермического потока от точки к точке. В соответствии с существующими программами глубинного бурения можно осуществить точные инклинометрические измерения, которые позволят раскрыть характер распределения вертикальной скорости движения льда. Это важно для расчета внутреннего тепла, производимого вязким трением, и его влияния на профили температуры.

Поскольку требуется большое количество данных о температуре и скорости массы льда в зависимости от глубины для дополнения сведений, полученных с помощью глубоких буровых скважин, очень полезными могут оказаться новые методы, как, например, филбертовское зондирование для взятия расплава [105].