4.5. Положительная обратная связь между температурой и скоростью у основания движущейся массы льда

Рассмотрим теперь случай температурно - зависимого закона течения. По результатам измерений течения льда при тех значениях напряжения, которые мы рассматриваем [21, 80], было показано (см. подраздел 2.4), что закон течения льда можно представить в форме

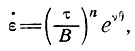
(30)

где θ -температура в °С, ν ≈ 0,1÷0,3 (°С)^-1.

Дифференциальное уравнение (23) теперь принимает вид

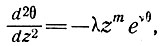
(31)

где

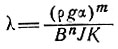
(32)

и

Наличие θ в правой части уравнения (31) делает его более сложным, чем в предыдущем случае.

Решение ищется в форме ряда и имеет следующий вид:

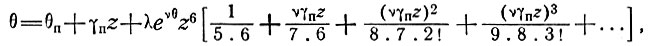
(33)

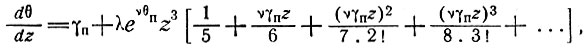
(34)

где θ_п, γ_п - температура и температурный градиент на поверхности (z = 0).

Значение γ_п в величинах температурного градиента у основания γ_ocн, который обычно известен из граничных условий, можно найти графически, как показано на рис. 4.6.

Таким образом, получаем значения γ_п из выражения

(35)

где Ф (γ_п) - возрастание потока тепла за счет внутреннего трения, определенное для некоторого диапазона градиентов на поверхности. Построив затем функцию γ_осн+Ф(γ_п) как функцию γ_п решение для γ_п получим как пересечение этих кривых. Теперь можно усмотреть, что при быстром возрастании функции Ф может возникнуть такое неустойчивое состояние, когда тепло, образующееся вследствие возрастания величины γ_п, не сможет отводиться именно в результате увеличения последней. Этот случай не имеет решения. Для небольших значений λ существует два решения, причем малое значение γ_п вообще устойчиво, в то время как высокое - неустойчиво. Если решения не существует, то это означает, что для заданных граничных условий не существует установившегося температурного профиля.

Как и ранее, используя типичные значения величины теплового потока, мы можем найти критические значения количества тепла, образующегося за счет внутреннего трения, выше которых решение становится неустойчивым. Для напряжения сдвига у основания величиной 1 бар это соответствует некоторой скорости, определяемой приведенным ниже уравнением (36). Значение критической скорости течения льда уменьшается с увеличением его мощности.

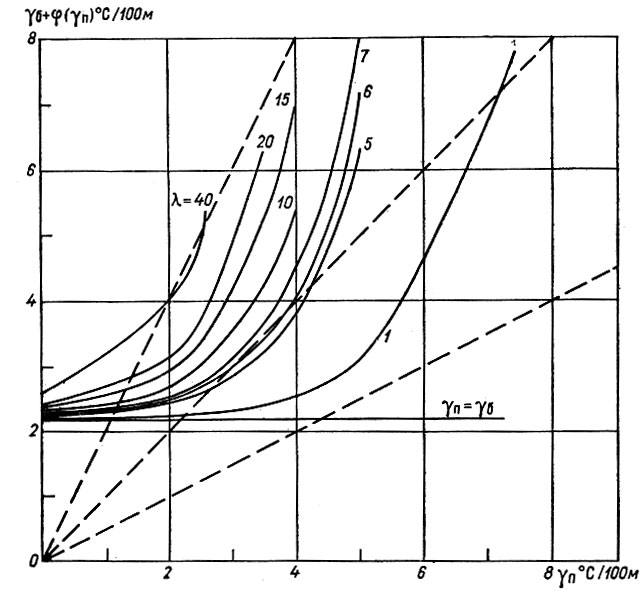
Рис. 4.6. Графическое решение поверхностного градиента температуры γ_п при его возрастании выше градиента температуры в базисном слое γ_б

Неустойчивость вызывается не тем, что температура льда достигает точки таяния, а тем что увеличение внутреннего теплообразования (пропорционального d²θ/dz²) становится слишком большим вследствие увеличения температурного градиента и тепло не может отводиться при этом увеличенном температурном градиенте.

Градиент скорости в массе льда определяется выражением

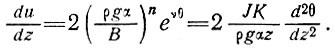
(36)

Используя зависимость (34), запишем

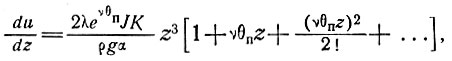
(37)

поскольку

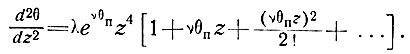
(38)

Отсюда, интегрируя, получаем

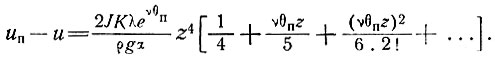
(39)

С помощью этого уравнения и принятых ранее величин параметров находим, что скорость на поверхности 1000-метровой массы льда равна примерно 8 м/год.

Следует отметить, что температурные кривые (см. рис. 4.4) вообще не согласуются с теми профилями температуры, которые к настоящему времени измерены (от поверхности до ложа) в холодных куполовых ледниках [14, 44]. Измеренные профили показывают сравнительно постоянные температурные градиенты в нижних слоях ледников. Это наводит на мысль, что внутреннее тепло, образующееся в этих слоях, пренебрежимо мало или же компенсируется влиянием других факторов, таких, как аккумуляция. Однако можно полагать, что скорость движения также небольшая. Чтобы полностью оценить влияние движения на температуру массы льда, очевидно, необходимо получить профили температуры в ложе ледника под движущимися массами льда. Как видно на рис. 4.4, существует лишь очень малая разница между профилями температуры в базисном слое (все тепло выделяется у основания) и внутренним нагреванием вследствие движения при температурно-зависимом степенном законе течения. Это различие становится очевидным лишь в непосредственной близости от основания.

Предшествующее рассмотрение согласуется с выводами Либутри [63] о том, что проблемы теплообразования вследствие внутреннего трения и аккумуляции при вертикальном движении могут в значительной мере рассматриваться как самостоятельные. Это является следствием того, что внутреннее трение возникает в основном в базисных слоях, где вертикальное движение пренебрежимо мало, в то время как аккумуляция и вертикальное движение главным образом связаны с верхними слоями, где нагрев за счет трения не существен. В следующем подразделе мы рассмотрим влияние поверхностной аккумуляции и вертикального движения льда на профиль температуры, пренебрегая внутренним трением или рассматривая его как часть возросшего температурного градиента в базисном слое γ_б*, т. е.

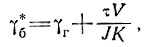
где γ_г - геотермический градиент во льду, τ - сдвиговое напряжение у основания, V - средняя скорость течения льда вниз по склону по длине ледника.