
4.4. Внутреннее нагревание ледника за счет грения и движения льда
Уже Лагалли [57] рассматривал нагревание льда за счет трения, возникающего внутри ледника при вязком течении, и пришел к выводу, что наибольшее количество тепла выделяется в области наибольшего сдвига, т. е. у ложа ледника. Изучение закона течения льда (см. раздел 2) наводит на мысль, что нагревание льда за счет трения приводит к более высоким скоростям деформации и, следовательно, увеличению внутреннего нагревания ледника и таким образом к возникновению сильной положительной обратной связи. Это предположение относится к случаям скольжения и катастрофического продвижения ледников, которые здесь не рассматриваются [62,66, 139, 140, 144 - 146].
Теперь попытаемся определить нагревание за счет трения и последующее влияние его на течение льда. Для этого рассмотрим поведение холодных масс льда в зависимости от температуры в области, где она ниже точки таяния, определяемой соответствующим давлением. Известно, что в ледниках умеренных широт при температурах вблизи точки таяния трение, возникающее в результате движения, вызывает только таяние, но не приводит к каким-либо температурным изменениям.
Робин [115] и Енсен и Радок [47, 48] при определении температурного градиента в базисном слое учли тепло, вызванное трением, и геотермический тепловой поток. С учетом методов расчета профилей скорости, рассмотренных в подразделе 4.3, этот способ представляется приемлемой аппроксимацией, корректность которой должна возрастать по мере приближения характера движения льда к глыбовому скольжению. Робин [115] указывал, что средний геотермический поток, равный 38 кал/(см2 o год), эквивалентен энергии, высвобождающейся в результате трения у ложа при напряжении сдвига в базисном слое 0,88 бара и движении со скоростью около 18 м/год. Этот результат получается из общего уравнения для расчета нагревания вследствие трения в результате скольжения, откуда
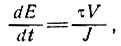
(4)
где 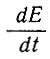 - количество тепловой энергии Е, высвобождающейся на единице площади в единицу времени t у основания; τ - напряжение сдвига в базисном слое; V - скорость движения льда над тонким базисным слоем, в котором, как предполагается, происходит сдвиг; J - механический эквивалент тепла.
- количество тепловой энергии Е, высвобождающейся на единице площади в единицу времени t у основания; τ - напряжение сдвига в базисном слое; V - скорость движения льда над тонким базисным слоем, в котором, как предполагается, происходит сдвиг; J - механический эквивалент тепла.
Либутри [63] вывел следующее выражение для общего теплового потока φ, обусловленного геотермическим тепловым потоком G и нагреванием за счет трения Г:
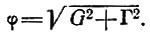
Температуру θ на глубине z Либутри определил из дифференциального уравнения
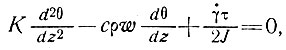
(5)
где К - теплопроводность льда, сρ - теплоемкость на единицу объема (удельная теплоемкость), ω - вертикальная скорость льда, J - механический эквивалент тепла, 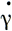 , τ - эффективные скорости деформации сдвига и напряжения сдвига для ламинарного течения. Отсюда получено выражение для температурного профиля в холодной массе льда, которое соответствует результату Робина [115] для моделей установившегося состояния:
, τ - эффективные скорости деформации сдвига и напряжения сдвига для ламинарного течения. Отсюда получено выражение для температурного профиля в холодной массе льда, которое соответствует результату Робина [115] для моделей установившегося состояния:
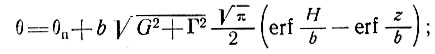
(6)
здесь θп - температура поверхности ледника, Н - толщина льда,
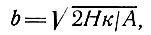
где А - скорость аккумуляции на поверхности ледника, к - температуропроводность льда.
Либутри [63] подробно рассматривает два особых случая применения уравнения (5): 1) для базисного слоя, в котором сосредоточена большая часть энергии внутреннего трения, где ω мала, и, следовательно, членом уравнения, в который входит cρω, можно пренебречь; 2) для верхних слоев ледника, где тепло от внутреннего трения льда можно рассматривать как дополнительный тепловой поток снизу. Поэтому третий член уравнения (5) может быть опущен, а его влияние учитывается возросшим температурным градиентом вблизи основания.
В первом случае этот исследователь принимает напряжение сдвига постоянным (его величину у основания) по всему деформирующемуся слою. Тогда из-за низких температур скорость деформации и результирующее количество тепловой энергии уменьшается по направлению вверх. Однако, как показано далее, при расчете рассеяния тепла необходим также учет уменьшения напряжения над базисным слоем.
Далее, развивая представления Либутри, учитываем тепло, выделяющееся в результате внутреннего трения на широком участке ледника и на больших расстояниях от его основания. Это применимо к медленно движущимся куполовым ледникам, не имеющим большого температурного градиента у основания [44]. При этом используется методика, изложенная ниже.
Холодная масса
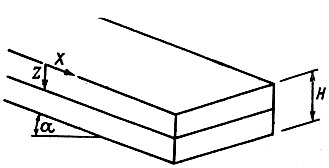
Рассмотрим холодную массу, очень широкую, с постоянной толщиной Н, движущуюся вниз на наклонной плоскости. Это течение является ламинарным. Поэтому скорость имеет только продольную составляющую, а градиент скорости направлен перпендикулярно ложу.
Возьмем ортогональные оси х в направлении движения и z в направлении вниз от поверхности ледника. Примем следующие обозначения: ρ - плотность льда, g- ускорение силы тяжести, θ - температура льда на глубине z, t - время, Q - количество тепла на единицу объема льда, К - теплопроводность льда, Е - энергия на единицу объема льда, с - теплоемкость льда (на единицу массы), к - температуропроводность льда.
Чтобы добиться ясного представления о факторах, влияющих на распределение температур в леднике, рассмотрим сначала отдельно несколько простых случаев, прежде чем исследовать суммарный результат для более общего случая куполового ледника, в котором взаимодействуют различные факторы. А пока сделаем допущение о равенстве нулю поверхностной аккумуляции и об установившемся распределении температур. Кроме того, не будем учитывать влияния нагрева поверхности ледника по мере его движения вниз по склону.
Температуры и скорости движения в массе льда, в которой тепло возникает за счет внутреннего трения, будут получены для следующих трех случаев:
1) в предположении ньютоновского вида закона течения льда (постоянная вязкость). Этот случай подробно рассмотрен Лагалли [57] и для низких напряжений и скоростей деформации (напряжение сдвига менее 0,5 бара; см. подраздел 2.3) представляет близкую аппроксимацию к действительному положению. Закон течения предполагается температурно независимым;
2) в предположении степенного закона течения льда. Это позволит оценить влияние нелинейности течения. Изменением закона течения под влиянием температуры вновь пренебрегаем;
3) в предположении температурно-зависимого степенного закона течения льда. При этом получается более сложное дифференциальное уравнение с сильной положительной обратной связью: большие сдвиговые напряжения вызывают более высокие температуры, которые в свою очередь приводят к еще более высоким скоростям сдвига.
4.4.1. Нагревание за счет внутреннего трения и движения льда для случая постоянной вязкости. В случае постоянной вязкости льда ???, не зависящей от напряжения и температуры, уравнение (17) п. 3.4.1 показывает, что для простой модели, описанной выше, скорость u на глубине z выражается следующим образом:
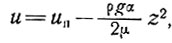
(7)
где uп - скорость движения поверхности ледника и
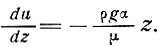
(8)
Так как все другие скорости отсутствуют, величина энергии, рассеиваемой на единицу объема льда вследствие вязкого трения, определяется из уравнения
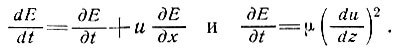
(9)
Но поскольку эта величина должна быть постоянной, то рассеяние энергии вдоль направления течения ∂Е/∂х = 0. Отсюда
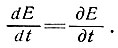
Рассмотрим небольшой образец льда толщиной δz на глубине z (см. рисунок). Так как поток тепла через лед выражается
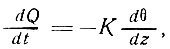
то для установившегося состояния получим
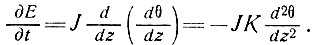
(10)
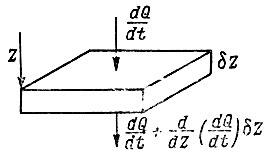
Образец льда
Для того чтобы профиль температуры не менялся во времени, необходим отвод тепла, выделяемого за счет вязкого трения, и в этом случае в некоторой точке (х, у), фиксированной в пространстве, выполняется соотношение
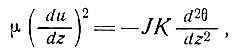
(11)
т. е.
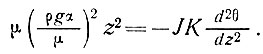
(12)
Интегрируя по z, получим
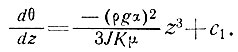
(13)
Далее, если для z = H (у ложа ледника), имеем
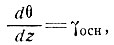
иначе говоря, температурный градиент вблизи основания ледника определяется геотермическим потоком (≈38 кал/см-2⋅год)), то
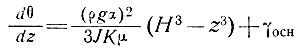
(14)
и
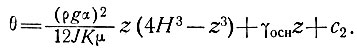
Если при z = 0, θ = θп, т. е. средней годовой температуре поверхности, тогда
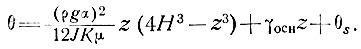
(15)
До сих пор предполагалось, что повсюду в леднике температура оставалась существенно ниже точки таяния при соответствующем давлении.
Если температура у основания - самая высокая, т. е. при z = H θ = θосн, то
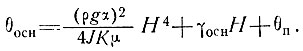
(16)
Условие, что температура у основания ледника остается ниже точки таяния, имеет вид θосн<0°С (или температура таяния при соответствующем давлении), т. е.
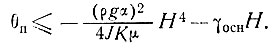
(17)
Если температура у основания достигает температуры таяния θт, то часть тепла расходуется на таяние, а именно [115]
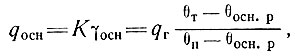
(18)
где qr - геотермический поток, θосн. р - расчетная температура у основания (из уравнения (16)). Температурный градиент у основания составит
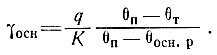
(19)
Результаты, полученные в этом разделе, можно подытожить следующим образом:
1) самая высокая температура имеет место у основания ледника;
2) самый высокий положительный градиент температуры должен наблюдаться у поверхности;
3) в отсутствие таяния тепловой поток у поверхности равен геотермическому потоку плюс общее количество тепла, выделяющегося при движении. Последнее равно потере потенциальной энергии льда при движении;
4) скорость изменения температурного градиента оказывается самой высокой у основания ледника;
5) наиболее важным результатом является вывод о том, что внутреннее трение приводит к образованию максимума в профиле температуры у основания ледника. До сих пор в расчетных профилях температуры максимумы не наблюдались (см. рис. 4.1а и 4.1б). Это наводит на мысль, что в исследованных в настоящее время профилях от поверхности до ложа более важную роль играют иные факторы, чем те, которые мы рассматриваем, или что образующееся внутреннее тепло для этих случаев пренебрежимо мало.
Однако к настоящему моменту получено лишь небольшое количество профилей температуры от поверхности до самого ложа, причем сведения о характере движения льда в этих случаях недостаточны. Следовательно, будет весьма ценным получение этих профилей до самого ложа в тех ледниковых районах, где измерена скорость движения ледника, а также вертикальный профиль скорости. Таким путем можно провести проверку как величин внутреннего нагревания ледника, так и геотермического потока с учетом свойств поверхности раздела лед - скальное ложе.
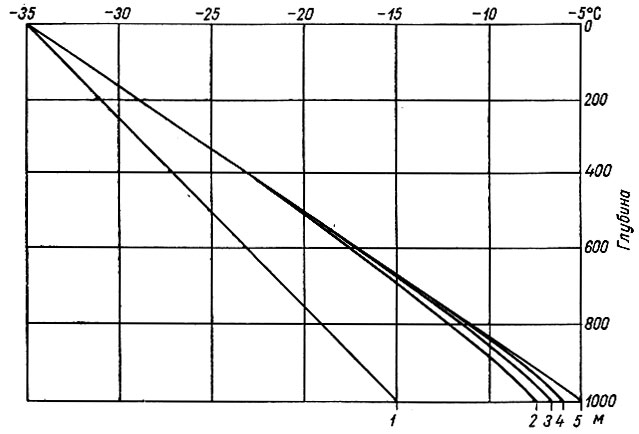
Рис. 4.4. Профили температуры нагревания вследствие трения при отсутствии других воздействующих факторов. 1 - нагревание отсутствует, 2 - нагревание при вязком течении, 3 - нагревание при степенном законе течения, 4 - течение по температурно - зависимому степенному закону течения, 5 - нагревание в базисном слое
Для определения величины образующегося во льду внутреннего тепла возьмем типичные значения параметров для массы льда и оценим разницу между градиентами в базисном слое и на поверхности этих масс, исходя из уравнения (14) для z=0:
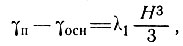
где
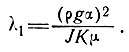
В качестве величин параметров примем: ρ = 0,917 г/см3, g = = 0,98·103 см/с2, α = 10-2, J = 4,2·107 эрг/кал, К = 5·10-3 кал/(см2 ×с·°С), μ = 1015 пз, Н=103 м.
Тогда γп - γocн = 1,16°С/100 м, что эквивалентно примерно 0,53 теплового потока, проходящего через базисный слой. На рис. 4.4 представлен типичный температурный профиль для простой модели этого типа.
Отношение потока тепла qz, образованного ниже некоторого уровня z, к общему потоку тепла на поверхности Q дано в табл. 4.2а.
Таблица 4.2а
Значения отношения qz/Q ниже уровня z
| z, м.......... | 0 | 500 | 800 | 900 | 1000 |
| qz/Q0/0..... | 100 | 87,5 | 49 | 27 | 0 |
4.4.2. Внутреннее трение и степенной закон течения льда. Рассмотрим случай степенного закона течения льда вида
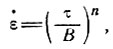
(20)
где 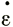 - скорость деформации сдвига, τ - напряжение сдвига, В и n = const (см. раздел 2).
- скорость деформации сдвига, τ - напряжение сдвига, В и n = const (см. раздел 2).
В этом случае для простой модели, описанной выше (см. подраздел 4.4), все еще имеем τxz в качестве единственного сдвигового напряжения и du/dz как единственную скорость деформации сдвига. Таким образом, величина рассеяния энергии выражается
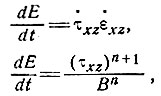
(21)
и поскольку
τxz = ρgαz
получаем
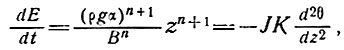
(22)
тогда дифференциальное уравнение принимает вид
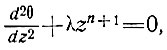
(23)
где
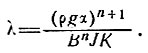
(24)
Отсюда, интегрируя, получаем
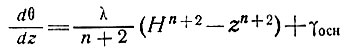
(25)
и
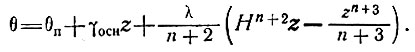
(26)
В частности, если n = 3, получим
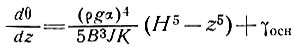
(27)
и
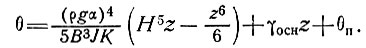
(28)
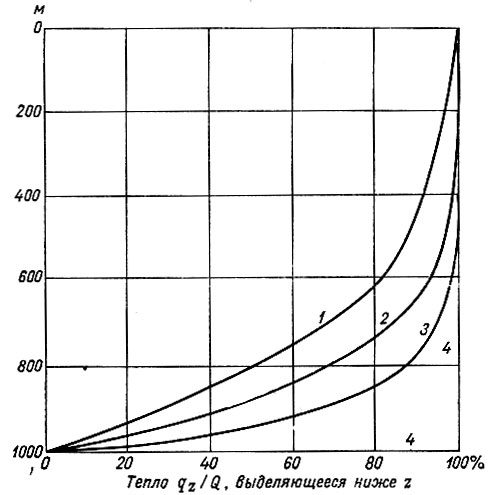
Рис. 4.5. Образование тепла вследствие внутреннего трения льда (для типов законов течения льда, приведенных на рис. 4.4). 1 - постоянная вязкость, 2 - степенной закон постоянной температуры, 3 - температурно - зависимый степенной закон, 4 - скольжение по ложу ледника
Таким образом, здесь справедливы те же качественные выводы, что и в п. 4.4.1. Кроме того, поскольку d2θ/dz2 пропорционально более высокой степени z, в нижних слоях ледника сосредоточено большее количество тепла, образовавшегося при той же потере потенциальной энергии, т. е.
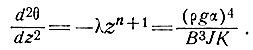
Следовательно, температурный градиент значительно меньше меняется в верхних слоях ледника, чем у основания (рис. 4.5). Теперь температура у основания определяется как
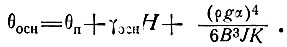
(29)
Третий член правой части выражения (29) определяет температуру у основания в результате движения. Далее имеем
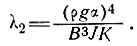
Затем, принимая такие же величины параметров, определяющих значения λ, как в п. 4.4.2, за исключением того, что μ = 1015пз, получим, что баланс теперь соответствует В = 109 бар/с1/3 [16, 17, уравнение (21)] и увеличение температуры в результате движения льда равно
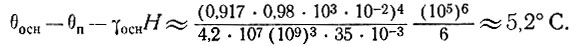
Возросший в любом слое ледника поток тепла, вызываемый движением льда, определяется формулой
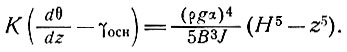
Образовавшееся суммарное количество потока тепла в леднике достигает величины, соответствующей градиенту температуры 0,63°С/100 м, или 0,39 геотермического потока. Вследствие высокой степени z в уравнении (27) наибольшее приращение потока тепла происходит в нижних слоях ледника. В табл. 4.26 для ледникового купола 1000-метровой толщины даны величины суммарного потока тепла, который возникает ниже этого слоя, а на рис. 4.4 показан типичный профиль температуры.
Таблица 4.2б
Значения отношения qz/Q ниже уровня z (тепло, образованное внутренним трением)
| z, м.......... | 0 | 500 | 800 | 900 | 950 | 990 | 1000 |
| qz/Q0/0..... | 100 | 97 | 67 | 41 | 23 | 5 | 0 |
По данным табл. 4.26 видно, что вклад в суммарный поток тепла от верхней части массы льда составляет лишь 3% нагрева за счет трения, вклад слоя от дна до 1/5 толщины (200 м) - 67%, а от нижних 100 м - свыше 40%. Сравнивая эти значения со значениями табл. 4.2а, видим, что высокостепенной закон течения льда играет весьма важную роль в концентрировании теплообразования у основания ледника.
|
ПОИСК:
|
© GEOMAN.RU, 2001-2021
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'