4.3. Влияние профиля температуры на профиль скорости движения ледника

Най [89, 90] установил, каким образом типичное температурное распределение, вычисленное для льдов Гренландии, влияет на вертикальные профили скорости деформации и скорости, рассчитанные по закону течения Глена [34] (рис. 4.2). Из раздела 2 следует, что простой степенной закон течения Глена, экстраполированный к малому напряжению, дает слишком заниженные скорости деформации. Вместе с тем высокая концентрация сдвига в придонных слоях достаточно очевидна и является следствием как большого сдвигового напряжения, так и более высоких температур у основания.

Рис. 4.2. Рассчитанные по глубине профили температуры θ, продольного σ_х, вертикального σ_у, сдвигового τ_ху и эффективного сдвигового τ напряжений, относительной скорости, скорости сдвиговой деформации γ и скорости продольной деформации r для одного положения на Гренландском куполовом леднике [89, 90]

Для иллюстрации непосредственного влияния распределения температур на профиль скорости на рис. 4.3 показаны относительные распределения скорости, рассчитанные для трех различных профилей температур по закону течения

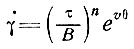
при равных скоростях на поверхности и равной нулю скорости у основания ледника.

По рис. 4.3 видно, что для вертикальных профилей температуры при условии, что самый теплый лед находится у основания ледника (обычный случай для холодных куполовых ледников), градиент скорости наиболее сильно выражен в самых нижних слоях. Следовательно, не очень существенно, является ли это движение быстрым сдвигом в чистом льду у основания, или только скольжением между поверхностями чистого льда и ложа ледника, или же, что более вероятно, быстрым сдвигом в смеси льда, песка и скальной породы в базисном слое (Хансен [44]). Най [89, 90] указывает, что дополнительное небольшое продольное напряжение по всей толщине льда оказывает не очень существенное влияние на вертикальный профиль скорости его движения.

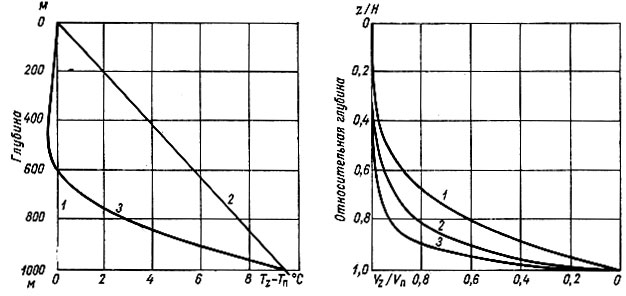
Рис. 4.3. Типичные профили относительной скорости V_z/V_s, расчитанные для куполового ледника Уйлкса толщиной 1000 м, где сдвиговое напряжение в базисном слое составляет 1 бар для изотермического (1), линейного (2) и рассчитанного (5) профилей температур (см. рис. 4.16) с использованием закона течения льда вида γ = (τ/В)ⁿ е^θ

Такой упрощенный подход нуждается в некоторых уточнениях. Робин [115] показал, что нагревание льда за счет трения при его движении может повлиять на профиль температуры. Енсен и Радок [48] в своих расчетах распределений температуры во льду использовали данные Робина, полученные простым суммированием общего нагревания льда за счет трения и геотермического теплового потока у основания. Правомерность такого подхода становится очевидной по мере уменьшения толщины слоя.