4.2. Рассчитанные профили температуры

Если бы масса льда была неизменной (без какой-либо аккумуляции и движения), ее профиль температуры представлял бы прямую линию, параметры которой определяются средней температурой на поверхности ледника и температурным градиентом, соответствующим геотермическому потоку тепла у основания ледника, или же температурой у основания в том случае, если бы в этой области она достигала точки таяния при соответствующем давлении.

Такие процессы, как аккумуляция на поверхности, таяние льда у основания, вертикальное движение и деформация, горизонтальное движение, а также долговременные изменения климата, влияют на профиль температуры масс льда и обусловливают появление характерной выпуклой вниз кривизны измеренных профилей, а в некоторых случаях отрицательных температурных градиентов у поверхности.

Эти параметры входят в уравнения, которые определяют наблюдаемые во льдах температурные профили.

Уравнение и его решение, полученное Робином для температуры установившегося состояния 6 на высоте г над основанием ледника, имеют вид:

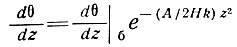
(1)

и

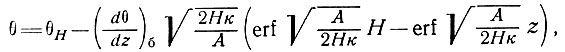
(2)

где Н - толщина льда, А - скорость аккумуляции, (dθ/dz)_б - температурный градиент в базисном слое, к - температуропроводность льда. Они довольно удобны для использования, так как содержат скорость аккумуляции на поверхности и уравновешивающее ее понижение уровня поверхности ледника, однако не учитывают горизонтального движения ледника и нагревания трением или неустановившихся изменений по его толщине. Робин получил также очень простой и полезный результат, определяющий зависимость отрицательной температуры поверхности ледника от градиента температуры по глубине, возникающего в результате горизонтального движения льда вниз к областям более высоких температур, в отсутствие теплопроводности, а именно

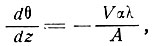
(3)

где V - скорость движения массы льда по склону, α - наклон поверхности, λ - скорость изменения температуры воздуха по вертикали.

Численные результаты Енсена и Радока [47, 48] учитывают как влияние теплопроводности, так и движение массы льда по склону. При использовании их данных с учетом реальной ситуации можно найти величины аккумуляции, скорости движения и толщины ледника, экстраполируя полученные ими кривые. Величины горизонтальных скоростей, которыми они пользовались, рассчитывались из уравнения неразрывности для установившегося состояния куполового ледника. Далее будет показано, что простое развитие их метода позволяет рассмотреть и случаи увеличения или уменьшения толщины куполовых ледников.

Влияние климатических изменений было исследовано Векслером [148] и Енсеном и Радоком [47], но, как мы увидим, известные профили температуры могут быть в значительной мере объяснены влиянием движения льда и аккумуляцией. Следовательно, именно эти факторы прежде всего являются предметом исследования, и только в случае несоответствия результатов имеет смысл изучение и учет изменений климата.

Поскольку закон течения льда обнаруживает сильную температурную зависимость, необходимо знание температурных распределений в массе льда для расчета распределения скорости.

Рассмотрим теперь влияние температурного профиля от поверхности до основания на соответствующий профиль скорости.