3.3. Симметрия ледника и разделение продольного и поперечного его движений

Одной из наиболее важных проблем динамики ледовых масс является определение изменения их продольной средней скорости вдоль линии тока. Как указывалось в разделе 1, результаты этих измерений можно использовать для определения изменения скорости движения ледовых масс во времени, исследования истории ледника, приращения его массы и т. д.

Профили других составляющих скорости движения (поперечной, вертикальной) не изменяются в столь больших пределах, и, следовательно, во многих случаях их можно принимать постоянными или рассматривать как медленно изменяющиеся параметры вдоль линии тока. Среднюю продольную скорость движения по поперечному сечению ледника не так легко измерить, как скорость движения масс льда на поверхности. Поскольку формы профилей поперечных скоростей изменяются весьма медленно вдоль линии тока, часто представляется возможным связать их среднюю скорость 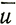с максимальной скоростью движения льда на поверхности u_п записав

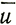= su_п

(12)

где s зависит от характера профиля поперечной скорости и определяется в значительной степени граничными условиями.

Рассмотрим теперь граничные условия трех основных типов ледниковых масс.

3.3.1. Глетчеры. Глетчеры обычно имеют небольшую горизонтальную дивергенцию и малую или нулевую скорость движения на боковых границах. В центре симметричного (по поперечному сечению) глетчера поперечный сдвиг равен нулю. Этот сдвиг увеличивается при удалении от центра и достигает максимума около границы ледника, где как продольная скорость, так и ее производные равны нулю, если нет непосредственного скольжения. Когда имеет место скольжение у основания или на боковых границах, оно становится еще одной величиной, которая должна войти в граничные условия.

3.3.2. Шельфовые ледники. Для шельфовых ледников можно принять скорость движения масс льда равной нулю у краев и постоянной от поверхности до основания. Самая большая скорость по поперечному сечению обычно наблюдается в центре. Величина u_у зависит в значительной мере от угла дивергенции границ. И снова скорости поперечной деформации сдвига вдоль центральной линии (а следовательно, и градиенты девиатора напряжений) равны нулю вследствие симметрии.

3.3.3 Куполовые ледники. Для идеально круглого куполового ледника на плоском основании линии тока представляют прямые линии, исходящие от центра. Горизонтальная дивергенция линий тока мала и зависит только от скорости течения в направлении движения и расстояния от центра. На практике неровности ложа вызывают конвергенцию линий тока (см. рис. 3.2); но если скорости дивергенции и конвергенции известны, то, как будет показано, влияние поперечных деформаций может быть учтено, если ввести их в расчет в виде параметров, медленно изменяющихся вдоль линии тока (см. подраздел 5.5).

И здесь скорости вертикальной продольной деформации сдвига 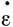_хz и скорости поперечной продольной деформации сдвига 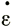_ху можно считать равными нулю на поверхности ледника. В идеальном случае форма профиля скорости мало изменяется в боковом направлении, т. е. под прямыми углами к направлению течения.

3.3.4. Общие результаты, вытекающие из условий симметрии. Вообще на границах ледовых масс нет скольжения, поскольку скорость этих масс равна нулю, причем градиент продольной скорости также равен нулю. Отсюда можно ожидать, что в точке максимальной скорости (т. е. в центре на поверхности ледника) градиент продольной скорости будет наибольшим. С другой стороны, градиенты скорости по поперечному сечению будут наибольшими на границах, где градиенты продольных скоростей наименьшие. Это дает основание предполагать, что можно исследовать раздельно поперечные напряжения и результирующие градиенты их скорости, с одной стороны, и вызываемые ими продольные напряжения, с другой.

В следующем разделе рассматриваются градиенты скорости по некоторому поперечному сечению сначала для ламинарного течения и нулевой скорости продольной деформации, а затем для постоянной скорости продольной деформации. После этого мы сможем исследовать изменение продольной скорости, вызванное изменениями продольного напряжения, причем величины скоростей и деформаций по поперечному сечению остаются постоянными или весьма медленно изменяются вдоль линии тока.