3.4. Поперечная скорость ламинарного течения

Профиль поперечной скорости ламинарного течения для глетчеров подробно был исследован Наем [84, 85, 87, 92, 93]. Дадим лишь краткое описание основных результатов его исследования.

Пусть оси координат расположены в центре поверхности ледника: х - в направлении движения, z - вниз и у - поперек ледника.

Для нулевого градиента продольной скорости 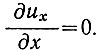. Для постоянной формы поперечного сечения u_y = u_z=0. Следовательно, единственными градиентами скорости, не равными нулю, являются 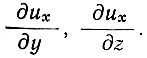. Из закона симметрии следует, что ???ух=0. Тогда, как было показано в подразделе 3.1, общие уравнения (1) сводятся к выражению (5)

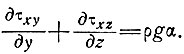
(13)

Принимая закон течения льда в виде

(14)

где

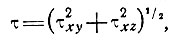
можно записать градиенты вертикальной и поперечной скоростей ламинарного течения в виде

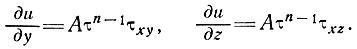
(15)

3.4.1. Особые случаи поперечных сечений ледников

1. Для ламинарного течения между двумя параллельными бесконечно глубокими вертикальными пластинами нет градиента вертикальной скорости, т. е.

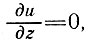
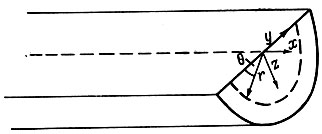
Рис. 3.3. Цилиндрический глетчер

и поэтому

Отсюда

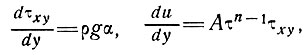
откуда получаем

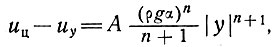
(16)

где u_ц - скорость в центре и uу - скорость на расстоянии у от центра.

2. Аналогично для ламинарного течения (бесконечно широкого) на плоском основании имеем

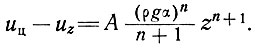
(17)

3. Для ламинарного течения в полукруглом канале примем цилиндрические полярные координаты с началом в центре поверхности ледника (рис. 3.3)

и получим следующие основные уравнения:

(18)

Когда течение не зависит от θ, получаем 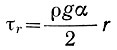и, следовательно,

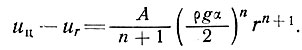
(19)

Най [92, 93] также дает неопубликованное ранее решение, полученное Честером методами теории возмущений, для формы поперечного сечения, несколько отличной от полукруга:

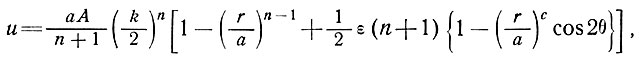
(20)

где k = ρg sin α и ε - увеличение горизонтального радиуса, большего, чем радиус круга, и

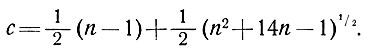
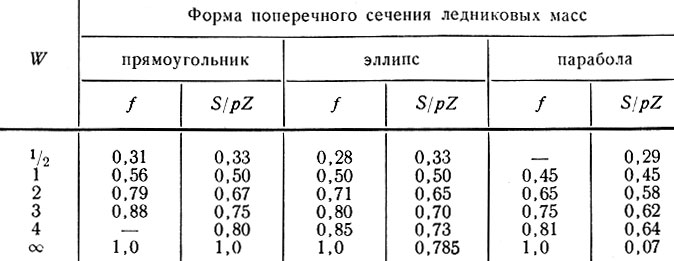
3.4.2. Численные решения для некоторых профилей поперечного сечения. Решая уравнения (13), (14), (15) при n = 3 численными методами, Най [92, 93] получил решения для скорости и напряжения сдвига при различных формах поперечных сечений ледниковых масс, таких, как парабола, эллипсы и прямоугольники (рис. 3.4 и 3.5). По результатам, полученным для напряжения сдвига и скорости движения, были вычислены величины коэффициента формы сечения f по приближенной формуле

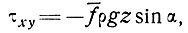
(22)

приведенные в табл. 3.1. Най установил, однако, что зависимость τ_хy от у отклоняется от линейной по мере приближения к границе ледника, причем степень отклонения зависела от формы его сечения. Приблизительные коэффициенты формы сечения для центральных профилей вертикальной скорости были определены ранее [16, 17, 74, 84, 85, 102] с помощью отношения

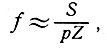
где S - площадь поперечного сечения глетчера, р - параметр поперечного сечения глетчера и Z - глубина в центре.

Рис. 3.4. Профили скорости U и напряжения сдвига Т по поперечному сечению в безразмерных единицах для прямоугольного (а), эллиптического (б) каналов и кубического закона течения льда [92, 93]

В табл. 3.1 приведены величины отношения S/pZ для прямоугольника, эллипса и параболы. Заметим, что при очень широких каналах величина S/pZ приближается к единице только для прямоугольника, в то время как рассчитанные Наем величины f очень быстро стремятся к единице. Представляется, что имеется хорошее согласие в величинах рассматриваемого отношения в области значений параметра W ≈ 1 (W - половина ширины ледника, деленная на его глубину). В то время как для больших значений W величина f>S/pZ, для малых значений W величина f<S/pZ.

Рис. 3.5. Профили скорости U и напряжения сдвига Т по поперечному сечению в безразмерных единицах для параболического канала и кубического закона течения льда [92, 93]

Следует помнить, однако, что кривые Ная (рис. 3.4 и 3.5) были рассчитаны с помощью закона течения льда вида

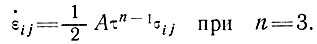
Если используется закон течения вида

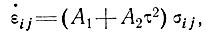
то влияние линейного члена A1 будет весьма существенным при малых напряжениях (менее 1 бара), которые встречаются в различных формах профилей глетчеров. Как следствие этого можно ожидать, что на практике коэффициент формы профиля ледника будет зависеть не только от формы поперечного сечения, но и от вида закона течения.

Величина f выбрана так, что истинная скорость на поверхности ледниковых масс получается интегрированием приближенных значений напряжения сдвига τ_xy = fρgαz вверх по оси z.

После того как определены коэффициенты формы сечения ледника в зависимости от формы профилей скорости поперечного сечения, возможно определение соответствующих величин параметров течения льда. Для этого целесообразно представить профили скорости по поперечному сечению в относительных координатах, как показано на рис. 3.6. Можно видеть, что изменяющиеся формы поперечного сечения вызывают заметные изменения формы поперечных профилей, но увеличение ширины за пределы W = 1 не влияет существенно на форму вертикального профиля. Для различных величин n в степенном законе течения должны получаться различные формы поперечных сечений. Следовательно, для широких глетчеров, имеющих эти сечения, форма сечения мало влияет на характер профиля вертикальной скорости. Это обстоятельство можно было бы использовать для определения параметра n. Для глетчеров с прямоугольной формой поперечного сечения или с крутыми боковыми поверхностями форма сечения мало влияет на вид профиля поперечной скорости. И в этом случае поперечный профиль вертикальной скорости можно использовать для оценки параметра n.

Рис. 3.6. Профили относительной скорости движения льда по поперечному сечению ледника, составленные по данным рис. 3.4а [92, 93]. а - парабола, б - эллипс, в - прямоугольник, г - комбинированные кривые для Y/Z = 1, д - комбинированные кривые для Y/Z = 2, е - формы поперечного сечения; 1 - прямоугольник, 2 - эллипс, 3 - парабола

Пальмер [97] дает численный метод для расчета верхней и нижней границ поперечного профиля скорости на поверхности ледника, а также для расчета средней скорости его течения.

Рис. 3.7. Измеренные профили поперечного сечения толщины льда (а) и скорости (б) на различных расстояниях вдоль глетчера Атабаска (см. рис. 6.1) [99]

Как упоминалось ранее, были измерены многие формы поперечных сечений глетчеров и определены поперечные профили их скорости. Весьма подробный ряд данных был получен Петерсоном (неопубликованные данные) для глетчера Атабаска (рис. 3.7). Эти результаты показывают, что поперечное сечение ложа глетчера относительно гладкое и медленно изменяется вдоль ледника. Они подтверждают выводы Ная [93, табл. IV], что средняя скорость течения льда на поверхности ледника и средняя скорость по поперечному сечению мало чувствительны к небольшим изменениям формы поперечного сечения, параметров течения и скольжения ледника по ложу.

Для определения распределения поперечной скорости реальных ледников при известной форме их поперечного сечения можно использовать интерполяцию или экстраполяцию численных решений Ная.