3.5. Влияние скорости продольной деформации на течение льда в поперечном сечении

3.5.1. Пластическое течение льда. Рассматривая течение льда по склону как пластический поток среды между двумя параллельными пластинами, движущимися раздельно или вместе с постоянной скоростью, Най [84, 85] получил решение для скорости двухмерного течения льда при наличии постоянного градиента продольной скорости течения льда от поверхности к основанию (скорость деформации) ледника.

Это решение при толщине льда h имеет вид:

(23)

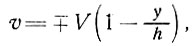
(24)

где u - горизонтальная скорость течения льда на расстоянии х вдоль его поверхности и глубине у, v - соответствующая вертикальная скорость, а С, V - начальные горизонтальные и вертикальные скорости соответственно. В этом случае вертикальный профиль горизонтальной скорости будет иметь форму эллипса, который остается постоянным вдоль линии тока. Изменение скорости вдоль глетчера объясняется изменением скорости скольжения 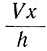у основания (см. рис. 3.10, n = ∞).

Это решение было использовано Наем при изучении профиля скорости течения льда вдоль ледника для установившихся состояний, т. е. при постоянной толщине льда и с изменениями, возникающими в результате полной компенсации течения льда увеличением аккумуляции или потерями вследствие абляции. При таком подходе течение льда в силу необходимости определяется характеристикой "аккумуляция - абляция". Более общее рассмотрение заключается в том, чтобы считать состояние равновесия независимым параметром и найти решение относительно скорости, которое определяется размерами массы льда, с учетом закона течения и граничных скоростей. Найденное таким образом распределение скорости течения льда можно сопоставить с характером аккумуляции и определить состояние равновесия и скорость изменения размеров куполового ледника. Этот подход используется в разделах 5, 6 и 7.

3.5.2. Степенной закон течения льда. Приняв более общий закон течения льда в виде 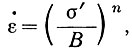, Най [87] получил распределение напряжений и скорости продольной деформации для канала эллиптической формы.

В этом случае уравнения оказались более сложными и простого аналитического решения для скорости продольной деформации получить не удалось. Однако оказалось возможным выразить решения для напряжения и скорости продольной деформации в значениях параметра "эффективного напряжения сдвига" т, определяемых формулой

(25)

Решения для напряжений, изображенных на рис. 3.8 по данным Ная [87], имеют вид

(26)

Эти профили показывают разницу между случаями отсутствия продольных напряжений и случаями течения сжатия и растяжения для различных значений n (рис. 3.9).

Решения для горизонтальной и вертикальной скоростей течения льда следующие:

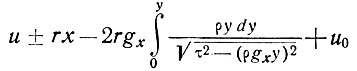
(27)

и

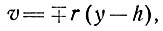
(28)

где r - постоянная скорость продольной деформации. Вводя безразмерные единицы

получим выражение для горизонтальной скорости

(29)

Оно иллюстрируется рис. 3.10а и 3.10б, на которых показано распределение скорости для различных значений параметра n.

Все это позволило Наю сделать ряд важных заключений.

1. Нулевая скорость продольной деформации. Из уравнений (27) и (28) находим, принимая г = 0, что скорость U определяется по выражению

и, кроме того,

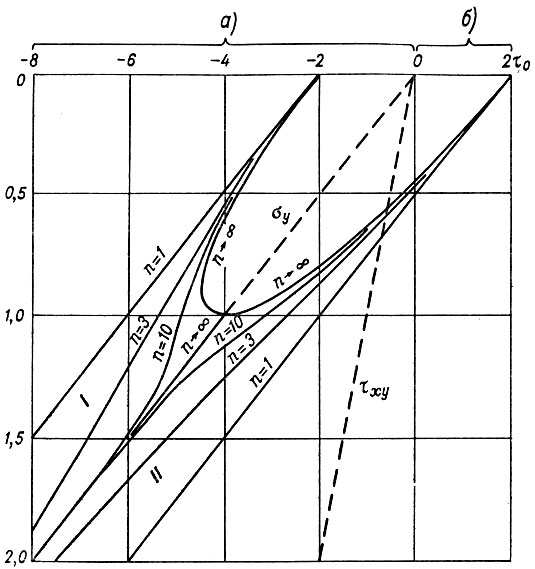
Рис. 3.8. Зависимость эффективного напряжения сдвига Т от глубины У (обе величины выражены в безразмерных единицах; при однородной плотности и степенном законе течения с принимается равным 1). Компоненты напряжения: а - сжимающие, б - растягивающие. I - течение сжатия, II - течение растяжения

Этот результат таков же, как полученный ранее [уравнение (17)] для ламинарного течения (т. е. при отсутствии продольных деформаций линии тока остаются параллельными).

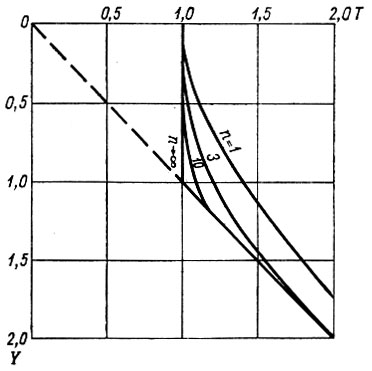
Рис. 3.9. Зависимость компонентов напряжения Т от глубины У (в безразмерных единицах при однородной плотности и степенном законе течения). Распределение σ_х дается двойным семейством полных кривых, каждая величина n дает одну кривую для течения растяжения и одну для течения сжатия. Распределения σ_у и τ_ху показаны пунктирными линиями и одинаковы при всех n. Все кривые приведены для наклона α = 14°2' (ctg α = 4), а единицы таковы, что с=1

Следовательно, можно ожидать, что решения уравнений для ламинарного течения будут хорошо соответствовать случаям небольших и пренебрежимо малых скоростей продольных деформаций.

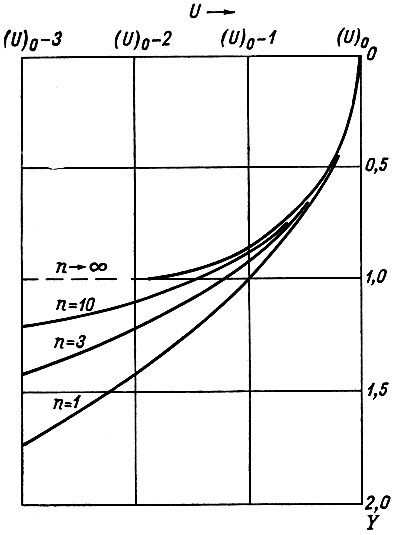
Рис. 3.10а. Зависимость продольной скорости U от глубины Y (в безразмерных единицах при однородной плотсности и степенном законе течения). Кривые приведены при Х=0; (U)_с - скорость на поверхности при Х=0; с принимается равным 1

2. Ньютоновская вязкость (n = 1). В этом случае профили горизонтальной скорости будут

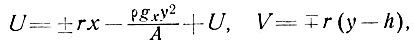
(31)

т. е. идентичны случаю скорости ламинарного течения. Следовательно, при значениях n, приближающихся к единице, скорость продольной деформации r не влияет на вертикальный профиль скорости.

3. Идеальная пластичность (n→∞) (напряжение текучести А = τ). В этом случае имеем

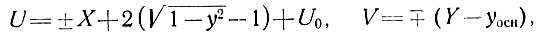
(32)

т. е. эллиптический профиль скорости, идентичный вертикальному профилю горизонтальной скорости в уравнении (23), которое было получено ранее для идеального пластического течения.

И, наконец, рассмотрим поперечное сечение глетчера и обозначим через V_п и 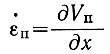продольные скорость течения и скорость деформации в центре поверхности ледника. Если допустить, что скорость продольной деформации изменяется аналогично скорости движения при удалении от центра поверхности, то на расстоянии r, где скорости движения и деформации будут V_r и _r, получим

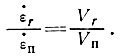
(33)

Далее, если закон течения имеет вид 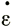= α_iτ + α₂τ_n (см. раздел 2), то при низких малых напряжениях течение льда будет приблизительно ньютоновским. Если скорость продольной деформации мала по сравнению со скоростью поперечной деформации на границе ледника, то, согласно выражению (33), скорость продольной деформации будет наибольшей в верхних слоях в центре, где поперечный сдвиг будет наименьшим. Следовательно, эти слои наиболее близки к ньютоновскому течению (малые скорости деформации). В базисном слое, где поперечный сдвиг большой, скорость продольной деформации мала. Таким образом, можно ожидать, что наличие скорости продольной деформации при этих обстоятельствах будет оказывать очень небольшое влияние на поперечные профили скорости и на среднюю скорость поперечного сечения, перпендикулярную к направлению течения. При больших скоростях продольной деформации, однако, задача точного определения ее влияния на профиль скорости поперечного сечения еще не решена (см. эксперимент со скважиной на леднике Юнгфрау [86]).

Для холодных масс льда условие постоянства скорости продольной деформации по всей его толщине в общем может быть не применимо, поскольку скорость у ложа этих масс может быть повсюду нулевой. В этом плане, может быть, более реалистично принять, что скорость продольной деформации связана с продольной скоростью движения льда так же, как и в выражении (33). Профиль скорости движения для такого условия еще не рассчитан, но при малых скоростях продольной деформации, которые, как показывают наблюдения, являются типичными для холодных куполовых ледников, можно ожидать, что влияние продольной скорости на вертикальный профиль этих ледников также пренебрежимо мало.

В этом разделе не учитывалась зависимость изменения закона течения льда от его температуры. Хотя это может быть и справедливо для ледников умеренных широт, для холодных масс льда, как будет показано далее, изменение температуры льда оказывает наибольшее влияние на профили скорости. Поэтому в разделе 4 мы рассмотрим изменение температуры вдоль холодных масс льда и влияние этого изменения на профили скорости.