3.2. Законы течения льда

Результаты изучения законов течения льда, изложенные в разделе 2, показывают, что скорость деформации ε_ij может быть связана с девиатором напряжения 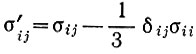отношением

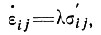
(6)

где λ - не константа, а функция напряжения сдвига, температуры, типа кристаллов и т. д. В некоторых случаях при небольших интервалах значений переменных, от которых зависит λ, закон течения можно выразить в достаточно простых формах, например

(7)

(n зависит от напряжения, А - от температуры),

(8)

(ki и k2 зависят от температуры),

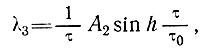
(9)

где

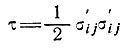
(10)

- эффективное напряжение сдвига (см. подраздел 2.1).

Идеальная пластичность льда может быть получена из общего степенного закона течения при условии приближения показателя n к бесконечности. Для случая постоянной ньютоновской вязкости показатель n равен единице.

Поскольку величина 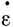_ij связана с градиентами скорости 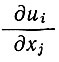выражением

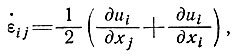
(11)

общие уравнения движения, записанные в значениях напряжения, при помощи закона течения могут быть преобразованы в уравнения, выраженные через значения скоростей движения. Эта процедура также потребовала бы преобразования граничных условий для напряжений в граничные условия для скорости или скорости деформации.

Общая задача решения уравнений движения относительно их скоростей с заданием граничных условий для скоростей и градиентов скорости очень сложна. Тем не менее для того, чтобы решить эту систему уравнений для трех основных типов масс льда, можно ввести некоторые упрощения благодаря таким особенностям их граничных условий, как симметрия, наличие областей нулевой скорости, свободные поверхности и т. д.