3. Основные уравнения движения льда и профили скорости по поперечному сечению

3.1. Общие уравнения движения льда в трех измерениях

При выводе уравнений движения массы льда выбирается следующая система ортогональных осей: ось х параллельна ложу (наклон которого равен ???) и расположена в плоскости движения, ось z направлена вверх и перпендикулярна ложу и ось у - нормаль к направлению движения.

Пусть σ_ij (i, j=x, у, z) - тензор напряжения в точках (х, у, z), причем

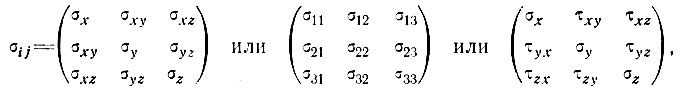
ρ - плотность льда и g - ускорение силы тяжести. Тогда для состояний равновесия или квазистатической ползучести имеем (пренебрегая силами инерции):

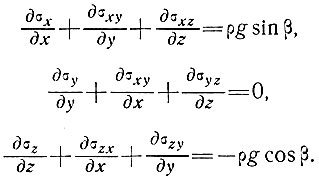
(1)

В общем, средний наклон ложа β в интересующем нас интервале достаточно мал, и поэтому справедливо приближение

Для частного случая, когда основание ледника плоское, β = 0 и уравнения сводятся к виду, рассмотренному Вертманом [139]. Этот вид уравнения удобен для изучения динамики свободно плавающих плоских айсбергов, но для шельфовых ледников и других ограниченных масс льда положение меняется, поскольку наклон их основания, так же как и изменение толщины в направлении свободной границы, существенно влияют на профили продольной скорости и деформации.

Наиболее важными являются два особых случая общих уравнений в трех измерениях.

Двухмерные уравнения продольного профиля.

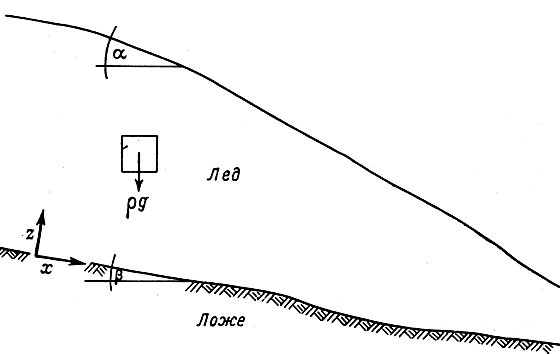
Рис. 3.1

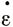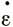Рассмотрим случай, когда все скорости деформации (_у, _ху, 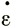_уz) равны нулю. Это обычно имеет место в точках, расположенных вдоль центральной линии на поверхности ледника, имеющего постоянную ширину, и если градиент продольной скорости пренебрежимо мал. Для центральной плоскости течения вследствие симметрии

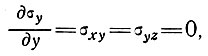
и, следовательно, остаются два двухмерных уравнения

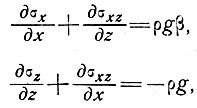
(2)

Как увидим далее (см. подраздел 3.3), благодаря симметрии течения естественных масс льда видоизмененная форма этих уравнений позволяет рассчитывать профили продольной и вертикальной скоростей течения льда. Анализ формы поперечного сечения дает возможность распространить это рассмотрение на случай движения в трех измерениях (см. подраздел 5.2).

Профили поперечного сечения. Если градиент продольной скорости мал (обычный случай для гладко текущих ледников, удаленных от областей нарушения, таких, как ледопады) и боковое растяжение отсутствует (как для течения в канале, имеющем постоянное поперечное сечение), то общие уравнения имеют вид

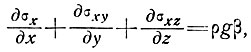
(3)

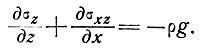
(3')

Эти двухмерные уравнения в большинстве случаев позволяют рассчитывать скорости по поперечному сечению и распределение напряжений.

Итак, поскольку нет ни продольного, ни поперечного растяжения, имеем

таким образом, используя уравнение (3') и интегрируя профили поперечного сечения от ложа до поверхности, при z = Z получим

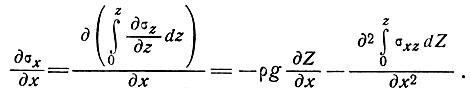
Так как наклоны основания и поверхности ледника постоянны, второй член в правой части этого уравнения, который можно записать в виде 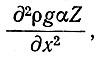, равен нулю. Отсюда

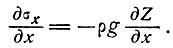
(4)

Следовательно, согласно выражениям (3) и (4), уравнения движения массы льда, относящиеся к профилям поперечного сечения, принимают вид

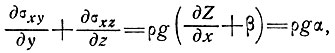
где α - наклон поверхности, который принимается постоянным по сечению. Решение этого уравнения для различных форм поперечного сечения было исследовано Наем [92, 93] и будет рассмотрено в подразделе 3.4.

В общем, уравнения движения нужно интегрировать с учетом граничных условий. Типичные границы масс льда для трех основных типов ледников, рассмотренных в работе, показаны на рис. 3.2.

Из-за того что масса льда деформируется, граничные напряжения недостаточно известны, но граничные скорости обычно можно определить. Поэтому необходимо преобразовать уравнения движения, выраженные через напряжения, в уравнения, в которых фигурируют скорости движения и деформации, что можно сделать, если использовать законы течения льда.

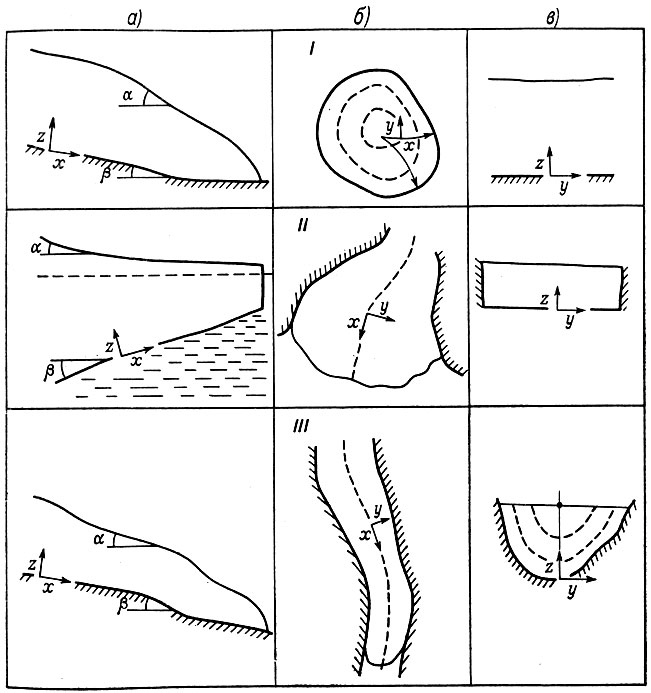
Рис. 3.2. Типичные границы трех основных типов ледниковых масс. а - профиль, б - план ледника, в - поперечное сечение, I - куполовый ледник, II - шельфовый ледник, III - глетчер