2.6. Скорость деформации по измерениям в естественно деформирующемся льду

Зависимость между скоростями деформации и напряжением в естественно деформирующемся льду изучалась многими исследователями по градиентам вертикальной и горизонтальной скоростей и скоростям сжатия скважин и туннелей в различных массах льда. С 1948 г. в некоторых глетчерах умеренного пояса были пробурены вертикальные скважины и определены вертикальные градиенты горизонтальной скорости от поверхности и почти до ложа [31, 72, 74, 100, 101, 120] (рис. 2.8).

Градиенты напряжения или давления, действующие в поперечном сечении ледников и создающие градиенты скорости движения, зависящие от глубины, были связаны с формой и размерами массы льда (см. раздел 3). Эти исследования позволили оценить октаэдрическое сдвиговое напряжение и скорости деформации сдвига и сравнить связь между ними с зависимостями, полученными в результате лабораторных измерений (см. рис. 2.2). До сих пор большая часть данных касалась лишь ледников умеренной зоны, за исключением результатов, полученных Уилсоном [151] для склона ледника Туто в Гренландии. Патерсон [100, 101] указывает на трудность их истолкования с использованием простой теории ламинарного течения из-за наличия продольных напряжений. Однако поскольку продольные напряжения и изменение скорости продольного напряжения с глубиной до сих пор мало известны, теорию ламинарного течения можно рассматривать в качестве первого приближения. Следует ожидать очень хорошего согласования с лабораторными результатами в тех случаях, когда скорости продольной деформации малы. Приведенные на рис. 2.2 результаты различных полевых измерений обнаруживают весьма хорошее согласие с лабораторными измерениями, особенно если учесть большой разброс в последнем случае измерений.

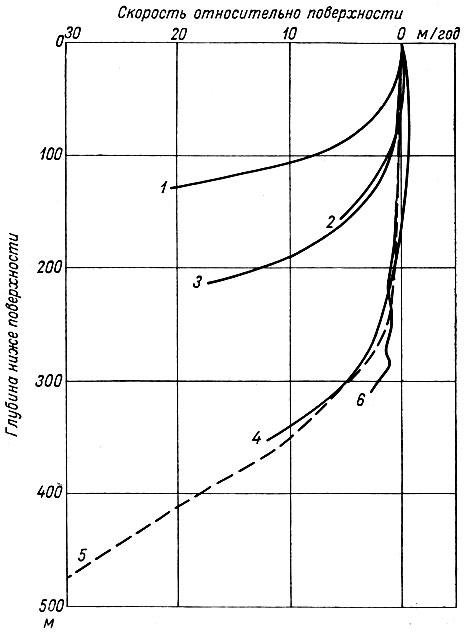
Рис. 2.8. Изменение скорости движения ледника с его глубиной относительно скорости движения поверхности для различных глетчеров. 1 - Юнгфрауйох (глубина 128 м), 2 - Голубой (155 м), 3 - Атабаска (209 м), 4 - Атабаска (340 м), 5 - Салмон (475 м), 6 - Маласпина (305 м)

Аналогичные результаты измерений градиента поперечной скорости глетчера, полученные Мейером [74], Петерсоном и Сэвиджем [100, 101], служат дальнейшим подтверждением этой общей тенденции. Но поскольку в данном конкретном случае дело касалось малых напряжений, то погрешности измерений соответственно возрастают и дают большой разброс.

Как отмечалось ранее, результаты измерений на нарушенном льду вокруг туннелей и скважин не могут непосредственно сравниваться с естественными деформациями вследствие различий ориентации кристаллов и больших сдвигов, которые имеют место в этих случаях. Тем не менее, как это следует из рис. 2.2, результаты измерения скорости сжатия скважины, полученные на ст. Бёрд [37, 38] и на ст. Кэмп-Сенчури [43], в сущности согласуются с результатами лабораторных измерений и являются ценной информацией о скоростях деформации при низких температурах, встречающихся в холодных ледниковых куполах. Здесь следует отметить, что формула Ная [86] для скорости сжатия

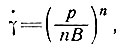
(γ - скорость деформации сдвига, τ = р/n - напряжение для перегрузочного давления р, В и n - параметры закона течения) требует постоянства величины n для определения напряжения сдвига и справедлива лишь в диапазоне значений р, для которых n - константа.

Имеющие особенно важное значение данные о законе течения льда в естественных ледовых массах получаются при полных измерениях динамики небольших куполовых ледников. В частности, следует указать, что помимо использования вертикального и поперечного градиентов скорости для определения параметров течения льда, в данном случае можно также использовать градиенты продольной скорости. Эта работа имеет более сложный характер и излагается подробно в разделах 5 и 6.