
Вращение Земли по инерции (движение полюсов Земли)
Введем понятие об эллипсоиде инерции. На расстоянии l от оси z возьмем материальную точку с массой m. Произведение массы точки на квадрат расстояния ее от этой оси называется моментом инерции точки относительно оси z.
Если имеются тело и ось, то сумма произведений массы каждой частицы этого тела на квадрат ее расстояния от оси называется моментом инерции тела относительно оси.
Возьмем какое-нибудь тело и проведем через любую из его точек неограниченное число осей. Можно определить моменты инерции тела относительно каждой оси; все они различны. Например, если взять однородный трехосный эллипсоид, то моменты инерции его относительно осей:
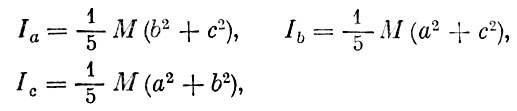
где а, b, с - полуоси трехосного эллипсоида, а М - его масса.
Проведем через любую точку в теле прямую. В обе стороны от нее отложим отрезки, равные единице, деленной на корень квадратный из момента инерции тела относительно этой прямой. Если сделать такое построение для большого числа прямых, проходящих через взятую точку, то концы отрезков будут находиться на различных расстояниях от точки, так как каждой прямой соответствует свой момент инерции. Но концы этих отрезков расположатся на одной поверхности, которая будет иметь форму эллипсоида, какой бы ни была форма самого тела. В общем случае это будет трехосный эллипсоид, в частных случаях - эллипсоид вращения, или шар. Такой эллипсоид называется эллипсоидом инерции тела. Каждой точке тела соответствует свой эллипсоид инерции.
Если в качестве исходной возьмем не любую точку тела, а его центр тяжести, то в этом случае эллипсоид инерции называется центральным эллипсоидом инерции, являющимся наибольшим из всех возможных. Три взаимно перпендикулярные оси эллипсоида инерции (наибольшая, наименьшая и средняя) называются главными осями. Моменты инерции относительно этих осей называются главными моментами инерции. Они обозначаются A, В и С (А > В > С). Эллипсоид инерции есть условная, воображаемая поверхность или геометрический образ, наглядно иллюстрирующий изменение величины момента инерции тела относительно различных осей. Момент инерции относительно наименьшей оси эллипсоида инерции есть наибольший из всех моментов инерции.
Для центра шара или куба эллипсоид инерции будет шаром; для тела, имеющего форму эллипсоида вращения, эллипсоид инерции также будет эллипсоидом вращения.
Если тело не абсолютно твердое и в нем происходят различные деформации и даже перемещения масс, то будут изменяться моменты инерции, а значит изменятся и эллипсоид инерции, и направления его главных осей.
Мы не знаем, как образовалась Земля, но знаем, что в процессе ее формирования тяжелые элементы сгруппировались около центра Земли концентрическими слоями; более легкие породы образовали всю периферию земного шара. По-видимому, в процессе формирования вследствие вращения Земли ее поверхность приняла форму сплюснутого эллипсоида вращения и, вероятно, внутренние слои одинаковой плотности представляют собой также эллипсоиды, похожие на эллипсоид наружной поверхности.
Поэтому можно с большой вероятностью допустить, что центральный эллипсоид инерции Земли является сплюснутым эллипсоидом вращения. В процессе его образования в силу причин, нам неизвестных, ось вращения Земли и главный момент количества движения (вектор) не совпали с малой осью эллипсоида инерции Земли. В результате этого на поверхности Земли (рассматривается одно полушарие) в районе полюса вращения образовались три особые точки, а именно: полюс инерции С - точка пересечения наименьшей оси центрального эллипсоида инерции Земли с поверхностью последней; полюc вращения Р - точка пересечения мгновенной оси вращения Земли с ее поверхностью; полюс главного момента G - точка пересечения главного вектора момента количества движения Земли относительно ее центра масс с поверхностью Земли.
Если в точке Р построить касательную плоскость к эллипсоиду вращения Земли (рис. 9), то вектор главного момента количества движения OG будет перпендикулярен этой плоскости.
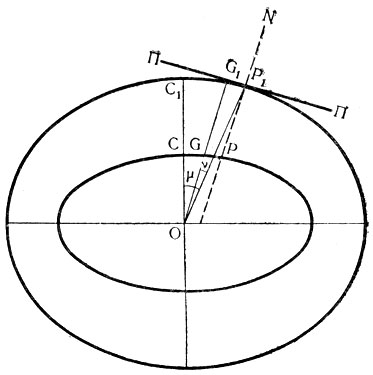
Рис. 9. Три особые точки на эллипсоиде инерции: С - полюс инерции; Р - полюс вращения ; G - полюс главного момента
Рассмотрим вращательное движение Земли как свободного твердого тела около центра ее масс при отсутствии внешних сил (по инерции). Возьмем подвижную систему координат Oxyz, связанную с Землей, начало которой совместим с центром масс Земли, а оси направим по главным осям эллипсоида инерции. В этом случае можно определить вращение Земли и положение ее мгновенной оси вращения в теле Земли относительно главных осей.
Изменение положения мгновенной оси вращения Земли описывается математическими уравнениями Эйлера. Иа них находят переменные ωx, ωy, ωz - проекции мгновенной угловой скорости ω на подвижные оси, связанные с Землей. По этим проекциям вычисляется мгновенная угловая скорость вращения Земли
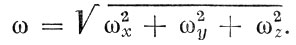
. Решение уравнений Эйлера приводит к выводу, что скорость вращения Земли около мгновенной оси вращения ОР постоянна и что скорость вращения самой мгновенной оси вместе с Землей около наименьшей оси эллипсоида инерции ОС тоже постоянна. Мгновенная ось вращения Земли ОР описывает внутри Земли около мгновенной оси инерции ОС конус с круговым основанием. Период вращения Земли около мгновенной оси вращения ОР - звездные сутки, период обращения около оси инерции ОС равен
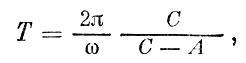
где ω - мгновенная угловая скорость вращения Земли около оси ОР, 2π/ω - звездные сутки, А и С - главные моменты инерции.
Мы не имеем возможности привести здесь решения уравнений Эйлера и ограничимся лишь геометрической интерпретацией этого явления.
Пусть фигура, изображенная на рис. 9, представляет сфероид (внутренний) и эллипсоид инерции Земли. ОСС1 - наименьшая ось сфероида и эллипсоида инерции Земли, ОР - мгновенная ось вращения Земли, ПП - касательная плоскость к эллипсоиду инерции в точке Р1 OG - главный момент количества движения (перпендикуляр к плоскости ПП). Если на вращающееся тело не действуют внешние силы, то его главный момент количества движения остается постоянным по величине и направлению. Это - одно из основных положений динамики. Следовательно, и плоскость ПП будет по отношению к центру О неизменна в пространстве. Поэтому при движении тела его эллипсоид инерции все время катится без скольжения по плоскости ПП, касаясь ее в точке Р1. При этом ось ОР описывает в теле Земли два конуса.
Возьмем неподвижный в пространстве конус с осью OG (рис. 10) и круглый конус с осью ОС, связанный с Землей. Угол при вершине у первого конуса 2POG, у второго - 2РОС. Широкий конус внутренней поверхностью зацепляет узкий и катится по нему, а ось OG остается все время неподвижной в пространстве, т. е. направлена в одну точку неба. Следовательно, узкий конус как бы вращается на оси OG. Поэтому большой конус вследствие вращения Земли бегает вокруг неподвижного маленького, а центр большого конуса С движется по кругу, обозначенному пунктиром. Общая образующая конусов ОР есть мгновенная ось вращения Земли. В движении, которое происходит против часовой стрелки, если смотреть с северного полюса неба, точка Р описывает два круга - основания конусов: круг с центром С и круг с центром G. Один оборот Земли вокруг G (звездные сутки) происходит за время, когда С совершит одно обращение вокруг G по пунктирному кругу. Точка Р пройдет полную окружность - основание большого конуса за столько звездных суток, сколько окружностей малого конуса содержится в окружности большого конуса или сколько радиусов основания малого конуса содержится в радиусе основания большого. Так как большой конус связан с Землей, то на поверхности Земли точка С и большой круг с центром в С неподвижны и малый круг с центром G катится по внутренней поверхности большого круга с центром в С (рис. 11). В это время точка Р внутреннего соприкосновения кругов движется по кругу с центром в С против часовой стрелки. Точка Р есть северный мгновенный полюс Земли, точка С - северный полюс инерции. Значит, при вращении Земли полюс Земли все время движется вокруг полюса инерции, почему он и называется мгновенным полюсом вращения Земли.
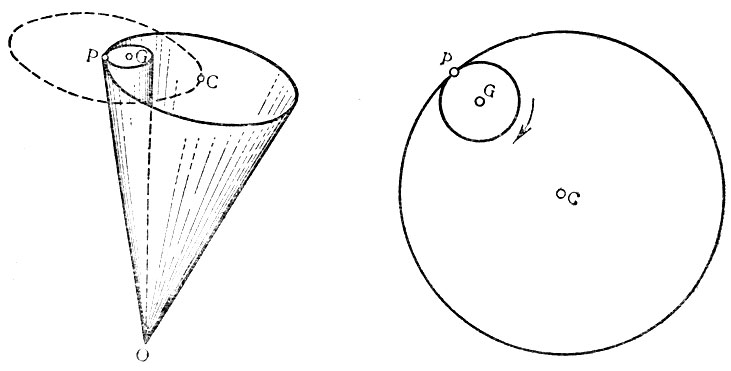
Рис. 10. Геометрическая интерпретация движения оси вращения Земли: OG - ось неподвижного в пространстве конуса; ОС - ось конуса, связанного с Землей; ОР - мгновенная ось вращения
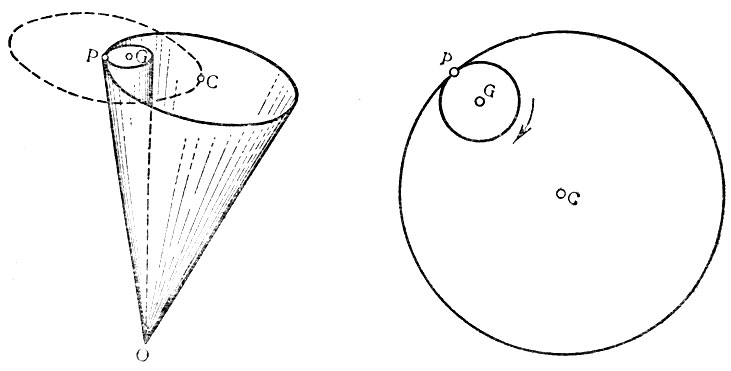
Рис. 11. Малый круг с центром G катится по внутренней поверхности большого круга с центром С
Причиной движения полюсов, а следовательно, и изменения широт, есть необходимое следствие того факта, что по условиям формирования Земли главный момент количества движения Земли OG не совпал с малой осью эллипсоида инерции Земли ОС, образовав с ней очень малый угол.
В самом деле, отношение радиусов СР:ОР вычисляется из формы меридиана эллипсоида инерции (см. рис. 9). С1, G1 и P1 лежат на одном меридиане эллипсоида инерции. Следовательно, ОС1, OG1 и ОР1 лежат в одной плоскости. OG1 - перпендикуляр к плоскости ПП и, значит, параллелен нормали к меридиану в точке Р1. Угол G1OP1 геометрически равен разности широт - астрономической (точнее, геодезической, но здесь астрономическая и геодезическая совпадают) и геоцентрической, а угол С1ОР1 аналогичен дополнению геоцентрической широты до 90°. Значит,
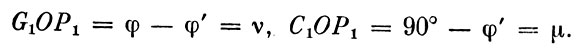
Но
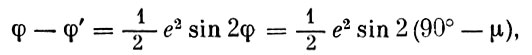
где е - эксцентриситет меридиана эллипсоида инерции. Так как угол μ мал, то с достаточной степенью точности имеем
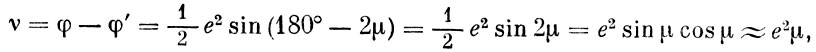
откуда
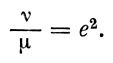
Оси эллипсоида инерции суть: большая - 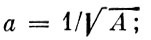 малая -
малая - 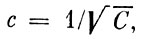 где A и C - моменты инерции Земли. По общему правилу
где A и C - моменты инерции Земли. По общему правилу

Значит,
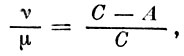
или

Время Т, за которое точка Р (см. рис. 9) опишет круг около полюса инерции С, вычисляется по формуле (4), где величина (С - А)/С получается из теории прецессии и нутации, и ее численное значение равно 0,003 272 37. Значит,

Следовательно,
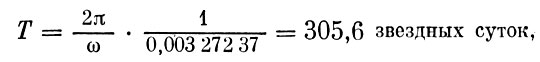
так как 2π;/ω = 1 звездным суткам. Следовательно, мгновенный полюс вращения Земли Р делает один полный оборот вокруг полюса инерции (точка С) за 305,6 звездных суток. Этот период впервые был получен Л. Эйлером, поэтому он и называется периодом Эйлера. Амплитуда периода, т. е. угол (90° - φ'), определяется только из астрономических наблюдений.
Все наблюдения со второй половины прошлого столетия и до последнего времени дают для угла (90° - φ') = μ величину от 0",1 до 0",3. Радиус GP должен быть в 305 раз меньше радиуса СР, т. е. меньше 0",001. Потому-то он из наблюдений и не получается, в силу чего принимается, что главный момент количества движения совпадает с мгновенной осью вращения Земли.
Период движения полюса, полученный из наблюдений, составляет 430 суток. Он называется чандлеровским по имени американского астронома С. Чандлера, впервые открывшего его. Расхождение периодов Эйлера и Чандлера происходит от того, что Земля - не абсолютно твердое тело, как это было принято Эйлером, а до некоторой степени упруга. Период Эйлера справедлив для абсолютно твердой Земли, чего нет в действительности. Период Чандлера справедлив для реальной Земли. Рассматривая движение Земли по инерции, мы принимали Землю как эллипсоид вращения, считая, что А = В. В действительности Земля несколько отличается от эллипсоида вращения; наибольший и наименьший радиусы экватора имеют разницу порядка 200 м. Что получится, если допустить, что А не равно 5, но мало отличается от него?
Подробный анализ уравнений, составленных для случая В - А не равно нулю, но весьма близко к нему при значении μ = (90° - φ') = 0",3, приводит к тому, что и в этом случае мгновенная ось вращения Земли будет описывать около оси С замкнутую коническую поверхность и движение мгновенного полюса по поверхности Земли остается тем же, как и при предположении, что А = В.
|
ПОИСК:
|
© GEOMAN.RU, 2001-2021
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'