Кинематическая картина прецессии и нутации

Здесь рассматривается вращение Земли и движение оси вращения в теле Земли опять-таки под воздействием двух пар сил, как это было в главе II, где давалась геометрическая интерпретация прецессии и нутации.

Рассмотрим движение главных осей инерции, связанных с Землей относительно неподвижной системы координат Оξηζ. Возьмем начало О неподвижной системы координат в центре тяжести Земли; пусть плоскость ξОη совпадает с плоскостью эклиптики для определенной эпохи, ось ξ направлена в точку весеннего равноденствия для той же эпохи, ось ζ - к северному полюсу эклиптики. Оси подвижной системы O_xyz, как и в предыдущем параграфе, направим по главным осям эллипсоида инерции Земли, причем ось O_z направлена по наименьшей оси, главный момент инерции относительно которой является наибольшим.

Положение подвижных осей относительно неподвижных задается для каждого момента тремя углами Эйлера - ψ, φ, 0 (ψ - угол, составленный линией пересечения плоскостей ON с осью Оξ, φ - угол, составленный той же линией с осью О_х, и 0 - угол между осями O_z и Oζ). Прямая пересечения плоскостей ON называется линией узлов, угол ψ - углом прецессии, о - углом нутации и φ - углом собственного вращения. Подвижная система координат O_xyz может быть совмещена с неподвижной Оξηζ тремя поворотами относительно трех соответствующих осей: поворотом на угол ψ около оси Оζ, на угол О вокруг оси ON и на угол φ около оси O_z (рис. 12).

Таким образом, если известны углы ψ, О, φ на каждый момент времени, то известны и положения главных осей инерции в эти моменты, а следовательно, и положение Земли и ее мгновенной оси вращения в пространстве.

Изменение угла поворота за единицу времени есть угловая скорость вращения, изображаемая стрелкой (вектором), направленной по оси вращения; в нашем случае изменения углов ψ, О, φ во времени (скорости) обозначаются , , .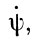

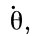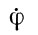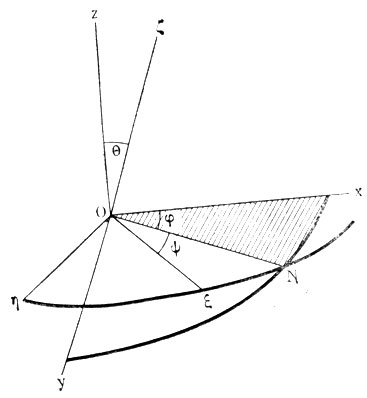
Рис. 12. Углы Эйлера: ψ - угол прецессии; О - угол нутации; φ - угол собственного вращения

Для определения этих величин составляются дифференциальные уравнения, включающие в себя 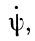, , 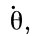, 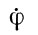а также ψ, О, φ и возмущающие силы со стороны Луны и Солнца.

В силу математических трудностей мы не можем показать, как из решения уравнений получаются угловые скорости 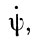, , 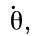, 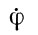характеризующие движение главных осей инерции относительно неподвижной системы координат, а следовательно, и движение оси вращения Земли. Однако мы можем охарактеризовать их смысл и привести геометрическую интерпретацию их сущности (рис. 13). ψ - угловая скорость - представляет собою изменение за единицу времени положения на эклиптике точки весеннего равноденствия. Иначе говоря, это - скорость оси вращения Земли вокруг оси эклиптики. От вращения изменяется угол прецессии ψ, вследствие чего ось ОР движется вокруг оси эклиптики по круговому конусу с периодом 25 729 лет. 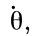- изменение за единицу времени наклона эклиптики, или скорость вращения около оси 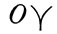, вследствие этого изменяется угол нутации О, т. е. угол наклона эклиптики к экватору. 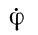- скорость вращения Земли относительно точки весеннего равноденствия вокруг наименьшей оси эллипсоида инерции ОС (собственной оси). Период этого вращения - звездные сутки.

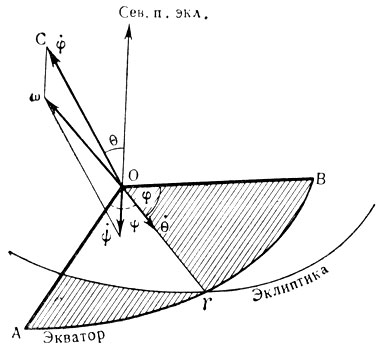
Рис. 13. Угловые скорости движения главных осей инерции:

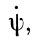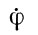Полное исследование скоростей и показывает, что каждая из них содержит по одной постоянной составляющей, к которой добавляется значительное количество (сумма) небольших периодических членов. Что же касается скорости вращения около оси 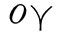- 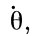, то она состоит только из суммы периодических членов. Малые периодические члены, входящие как слагаемые во все три скорости, называются нутационными, или просто нутациями.

Рассмотрим сначала регулярное вращение Земли, происходящее со скоростью 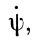. Постоянная составляющая этой скорости (коэффициент при времени в первой степени) именуется прецессией точки весеннего равноденствия 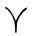по долготе. Она вызывает равномерное перемещение 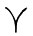вдоль эклиптики по часовой стрелке, если смотреть с северного полюса эклиптики (вследствие этого вектор прецессии 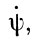направлен к южному полюсу эклиптики). Скорость прецессии 50",371 в год.

Равенство нулю постоянной составляющей 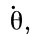свидетельствует о неизменности (в среднем) ε-наклона эклиптики к экватору. Постоянная составляющая 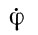- собственное вращение Земли, совершаемое с периодом в звездные сутки вокруг оси ОС против часовой стрелки, если смотреть с северного полюса Земли.

Векторная сумма постоянных составляющих 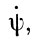, , 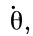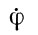и есть мгновенная скорость регулярного вращения Земли. Она не направлена по оси инерции ОС, хотя и очень близка к ней.

Прецессию и собственное вращение Земли можно интерпретировать следующим образом. Представим себе узкий круговой конус с вершиной в центре Земли, симметричный относительно оси инерции и прочно связанный с Землей (рис. 14). Представим далее второй круговой конус, центральная ось которого совпадает с осью эклиптики, с вершиной в центре Земли, но не вращающийся относительно эклиптики. При вращении Земли первый конус без скольжения катится по второму; жестко связанная с ним Земля вращается и прецессирует одновременно.

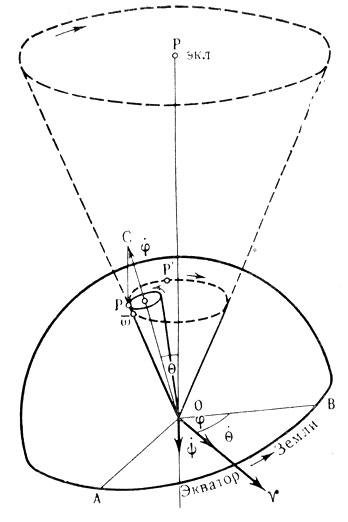
Рис. 14. При вращении Земли первый конус без скольжения катится по второму; жестко связанная с ним Земля вращается и прецессирует одновременно

Мгновенной осью вращения всегда является линия касания, или общая образующая конусов. Так как Земля вращается вместе с малым конусом, в теле планеты ее мгновенная ось вращения каждые сутки обходит по круговому основанию малого конуса вокруг оси инерции. Следовательно, полюс вращения Р перемещается по поверхности Земли. Это происходит тогда, когда начальное равномерное вращение около оси инерции нарушается внешней силой, в результате ось вращения отклоняется от оси инерции. В данном случае и появляется дополнительное движение оси вращения, накладывающееся на эйлеровское, вызванное возмущающими силами со стороны Луны и Солнца. Это перемещение составляет сотые доли секунды дуги, но когда дается качественная характеристика вращения Земли, оставить его без внимания нельзя. Так как оно обусловлено в основном прецессией земной оси - следствием притяжения Луны и Солнца, то его правильнее было бы назвать лунно-солнечным движением полюсов.

Нутационные члены в 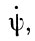, , 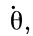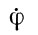искажают нарисованную стройную картину движения Земли. Нутация 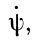и 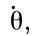- покачивания оси инерции и мгновенной оси вращения относительно эклиптики, благодаря чему оси в своем движении вокруг оси эклиптики непрерывно периодически отклоняются от конических поверхностей. Эти отклонения, выражаемые формулами, выводятся в небесной механике: они представляются суммами членов с синусами и косинусами по разным аргументам, а именно:

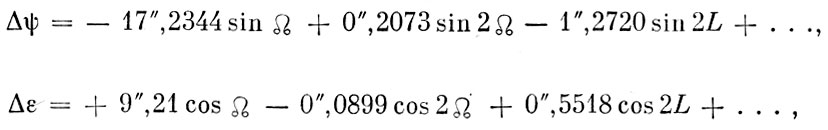
где Ω средняя долгота восходящего узла лунной орбиты, которая уменьшается равномерно с течением времени и изменяется на 2π за 18,613 года; L - средняя долгота Солнца, равномерно возрастающая со скоростью 2π за тропический год.

Нутация 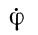- малое отклонение скорости вращения Земли от некоторого среднего значения.

В связи с движением в пространстве оси инерции ОС перемещается среди звезд и небесный экватор. За счет этого движения, а также за счет движения эклиптики, о котором речь шла ранее, происходит смещение точки весеннего равноденствия вдоль эклиптики, которое можно разделить на регулярное (лунно-солнечная прецессия) и периодическое (нутация). Лунно-солнечная прецессия, складываясь с прецессией от планет, дает полную gрецессию средней точки весеннего равноденствия 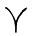. Лунно-солнечная прецессия и колебания плоскости эклиптики вызывают периодическое отклонение истинной точки весеннего равноденствия от средней. Истинная точка весны совершает относительно средней небольшие колебания как вдоль эклиптики, так и вдоль экватора. Амплитуда колебаний истинной точки весеннего равноденствия относительно средней по эклиптике составляет ±18", по экватору - примерно ±16". Амплитуда колебаний наклона эклиптики к экватору Де составляет ±10".