Движение центра масс системы Земля + Луна вокруг Солнца

Рассмотрим теперь движение Земли вокруг Солнца вместе с Луной, когда эти три тела взаимно притягиваются между собой по закону всемирного тяготения, когда силы обратно пропорциональны квадратам расстояний между ними. В отличие от случая, где рассматривалось движение одной Земли вокруг Солнца, здесь орбита Земли будет уже не эллипсом, а сложной кривой двоякой кривизны, т. е. такой кривой, все точки которой не лежат в одной плоскости. Заметим, что как орбита центра масс Земли, так и орбита центра марс Луны в своем движении вокруг Солнца всегда обращены к нему вогнутостью (рис. 3).

Полное решение задачи о движении Земли и Луны вокруг Солнца представляет такие трудности, что, несмотря на усилия величайших математиков XIX и XX вв., удалось получить решения только в некоторых частных случаях и то не в общем виде, а лишь привести к некоторым приближениям.

Предположим, что движение Луны так связано с движением Земли, что их общий центр масс движется вокруг Солнца по эллипсу. Хотя это и не вполне соответствует истине, но так как расстояние до Солнца настолько превышает расстояние от Луны до Земли и масса Солнца весьма велика, то погрешностями в нашем предположении можно пренебречь.

Положение центра масс системы Земля + Луна, или, как мы его будем называть в дальнейшем, барицентра, находим обычным путем (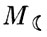 - масса Луны, 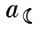- расстояние между Землей и Луной):

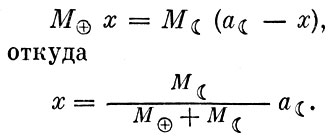
Среднее расстояние Луны от Земли 384 400 км, а масса Земли в 81,30 раза больше массы Луны. Исходя из этого х = 4670 км, т. е. центр масс системы Земля + Луна находится внутри Земли, ближе к ее поверхности, чем к центру.

За один месяц центр массы Земли описывает около барицентра эллиптическую орбиту, подобную орбите центра массы Луны вокруг центра Земли, только меньше ее в отношении 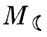 /( 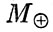+ 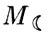) и повернутую в ее плоскости на 180°.

Вследствие движения вокруг барицентра Земли и Луны наблюдатель с Солнца увидит Землю, например, при фазе Луны первая четверть впереди барицентра, а через половину синодического месяца (14,76 средних солнечных суток) при фазе Луны последняя четверть - позади барицентра (рис. 4). Это так называемое лунное неравенство в движении Земли, период его равен синодическому месяцу, а величина L - 6",44. Такую же картину, т. е. такое же неравенство наблюдают с Земли в движении Солнца среди звезд. Но плоскость орбиты Луны в движении ее вокруг Земли не совпадает с плоскостью орбиты барицентра, а наклонена к ней под углом 5°9'. Поэтому центр Земли бывает то выше плоскости орбиты барицентра, то ниже ее. Наблюдателю из центра Земли предстает обратная картина: центр Солнца то ниже плоскости орбиты барицентра, то выше ее. Вследствие этого неравенства (величина его приблизительно 0",6) геоцентрическая широта Солнца не всегда в точности равна нулю. На рис. 5 S - центр Солнца, L - Луна в соединении с Солнцем, С - центр Земли и Т - барицентр. Наблюдатель из С увидит Солнце выше плоскости орбиты барицентра. Все описанные движения Земли усложняют наблюдаемое движение Солнца среди звезд.

Кроме сложного движения Земли, вызываемого наличием Луны, изменяются и другие параметры движения: линия апсид (прямая, соединяющая апсиды) и элементы орбит. Линия апсид вращается в своей плоскости в сторону движения Земли, из-за чего долгота перигелия орбиты ω, т. е. угол между направлением из Солнца на перигелий и точку весеннего равноденствия 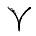, возрастает на 61",9 в год. В настоящее время долгота перигелия около 102°08'.

Что касается изменения элементов орбиты центра масс Земля + Луна вокруг Солнца, то можно сказать, что они очень устойчивы, вследствие чего орбита близка к эллипсу (движение кеплеровское). Лишь незначительно и то периодически изменяются большая полуось а, эксцентриситет е и средняя скорость, или, как говорят астрономы, среднее движение 2π/Р, где Р - период обращения. Эти элементы, называемые оскулирующими, показывают, что орбита постепенно меняет форму и размеры. Заметим, что если элементы орбиты движущегося по эллипсу тела не изменяются или изменяются периодически, то движение тела будет устойчивым, т. е. тело в таком же положении может двигаться сколько угодно долго. Если же элементы орбиты меняются прогрессивно, что, например, имеет место у движущихся близко к Земле спутников, то движение будет неустойчивым, а эллиптическая орбита тела способна превратиться в эллиптическую, но с другими элементами, спутник упадет на Землю.

Рис. 3. Движение Земли и Луны вокруг Солнца

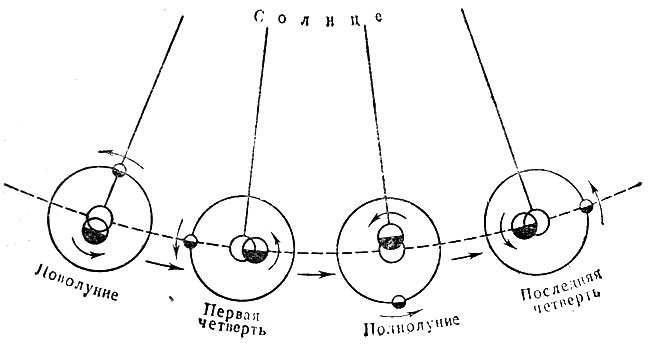
Рис. 4. Движение Земли и Луны вокруг барицентра и фазы Луны

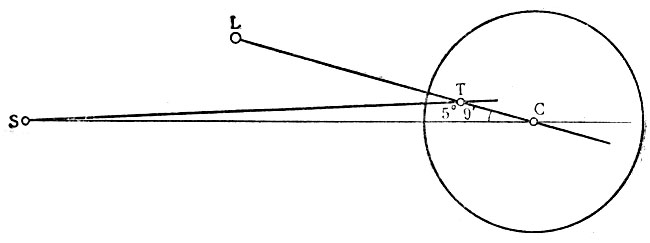
Рис. 5. Неравенство в геоцентрической широте Солнца

Зачастую спрашивают, долго еще Земля будет двигаться вокруг Солнца и не потерпит ли катастрофы, сойдя со своей орбиты? Иначе говоря, устойчиво ли движение Земли или, вообще говоря, солнечной системы.

Впервые проблему устойчивости солнечной системы поставил еще в начале прошлого века знаменитый французский ученый Лаплас. Он же доказал эту устойчивость, но не полностью, а только в первом и во втором приближениях. Во всяком случае вековые возмущения первого и второго порядков в больших полуосях больших планет солнечной системы отсутствуют. Другой французский ученый Лагранж также приближенно доказал, что вековые возмущения в эксцентриситетах и наклонностях орбит больших планет имеют колебательный характер и остаются достаточно малыми. Поэтому в настоящее время можно с уверенностью сказать, что изменения орбит больших планет солнечной системы в течение будущих десятков тысяч лет будут достаточно малыми. В частности, орбиты Земли и Луны вокруг Солнца мало отличались от современной на протяжении последней сотни тысяч лет.

В 60-х годах советские математики А. Н. Колмогоров и А. И. Арнольд доказали устойчивость системы тел, значительно отличающейся от солнечной. Арнольд построил также примеры систем, где в отдельных случаях может быть неустойчивость. Однако все эти результаты нельзя распространить на солнечную систему.

Если рассмотреть движение барицентра Т вокруг Солнца с учетом притяжения Земли и Луны другими планетами или, как говорят, возмущенное движение центра масс системы Земля + Луна, то картина движения несколько изменится. Под действием гравитационных возмущений центр масс системы Земля + Луна движется вокруг Солнца по орбите, близкой к эллиптической, но немного измененной (возмущенной) из-за притяжения Земли и Солнца планетами; вследствие этих возмущений движение центра масс системы Земля + Луна отклоняется от движения по законам Кеплера. Отклонения невелики: изменение долготы l, вызываемое Луною, не превосходит ±7",37, Меркурием ±0",05, Венерой ±17",57, Марсом ±7",02, Юпитером ±15",65, Сатурном ±1",04 (в общей сложности ±48",71). Отклонение широты не превышает ±0",8.