Приложение II

Закон течения льда с учетом градиентов продольного напряжения

Чтобы преобразовать уравнение градиента продольного напряжения в уравнение градиента скорости деформации, рассмотрим вновь закон течения льда.

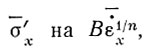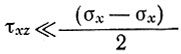Здесь достаточно лишь заменить если или если n ≈ 1. Главная задача заключается в том, чтобы определить связь между 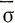'_х и 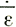_х, когда τ_xz не обязательно мало.

Мы отказываемся от формулирования степенного закона зависимости деформации для льда от напряжения, т. е.

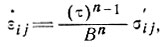
(1)

поскольку параметры n и В не постоянны с напряжением. Вместо этого мы принимаем отношение "обобщенной вязкости" вида

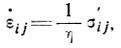
(2)

где η(τ, θ) - функция как напряжения, так и температуры.

Для октаэдрического сдвигового напряжения τ и скорости деформации 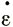из выражения (2) получаем

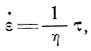
(3)

откуда

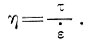
(4)

Это выражение можно рассматривать как альтернативное определение η. Уравнение (3) можно рассматривать как закон течения льда, и для каждой постоянной величины температура представляет отдельную кривую на диаграмме зависимости 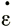от τ. Именно эти кривые мы и хотим определить.

Итак, подставляя для среднего девиатора продольного напряжения по колонке льда выражение 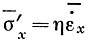в уравнение градиента напряжения

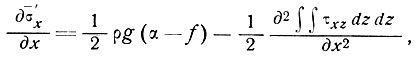
(5)

получаем

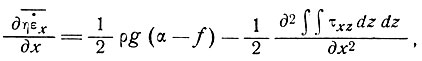
(6)

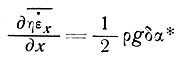
(как определение δα*), (7)

или

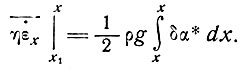
(8)

Определим теперь взвешенный средний параметр течения η* через вертикальную колонку льда как

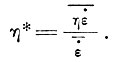
Теперь имеем для флуктуаций относительно средней величины (т. е. принимая 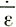_х1 = 0 при δα* = 0)

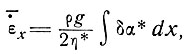
(9)

или

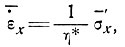
(10)

где

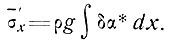
(11)

Отсюда для связи между продольным напряжением и скоростью продольной деформаци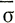и '_х и 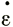_х получаем значение параметра η* для каждого τ и θ. Используем их теперь для определения закона течения в значениях октаэдрических величин.

Поскольку для октаэдрических величин 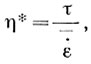, можем теперь получить закон течения льда, рассчитав 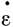по η и τ для каждой величины, и иллюстрировать это кривой 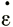как функцией τ.

Для двухмерного потока октаэдрическое сдвиговое напряжение τ рассчитывается из выражения

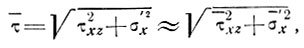
(12)

где

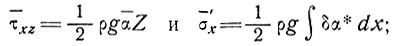
(13)

здесь 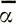принята как средний наклон поверхности на расстоянии х, примерно в 10 - 20 раз большем, чем толщина ледника.

Эти величины напряжения выводятся непосредственно по профилям измеренных высот и толщин льда" Скорость деформации на поверхности ε_п можно было бы измерить, однако для того чтобы получить среднюю скорость деформации по колонке, нужно иметь сведения, например, об отношении 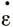_п/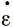_х = λ, для чего необходимо располагать сведениями о вертикальном профиле скорости. Однако если лед не скользит у основания, то мы можем ожидать, что скорость деформации будет изменяться с глубиной аналогично скорости V, т. е.

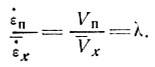
(14)

В холодных куполовых ледниках профиль скорости зависит от профиля температуры и поэтому удается выполнить его теоретические оценки (см. раздел 4).

При отсутствии сведений о профиле скорости можно допустить, что величина λ лежит между значениями ²/₃ и 1, приближаясь к 90% для типичных температурных профилей куполовых ледников. Отсюда можно записать в величинах измеренных скоростей поверхностной деформации

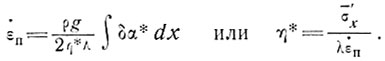
(15)

По измеренным изменениям скоростей поверхностной деформации 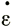_п и наклону поверхности α из выражения (15) можно определить обобщенную вязкость η*(τ, θ), а затем, пользуясь величинами среднего октаэдрического сдвигового напряжения из формул (12) и (13) и значениями средней температуры колонки в этом положении, определить положение точки 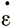(τ, θ) на кривой зависимости напряжения от скорости деформации, составив график 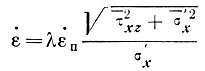как функции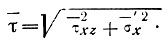

Чтобы получить полный ряд кривых для 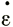(τ_z θ), требуются подробные данные о величинах 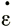_п, охватывающие широкий диапазон сдвигового напряжения τ и температуры θ.

Можно ожидать, что в ледниковых массах умеренных поясов зависимость продольной деформации от продольного напряжения определяется просто величиной октаэдрического сдвигового напряжения.