Приложение I

Вывод градиента девиатора продольного напряжения относительно продольной оси с произвольным наклоном

Рассматривается лишь двухмерное движение, или скорость плоской деформации.

Примем правостороннюю систему ортогональных осей х, z так, что горизонталь наклонена под произвольным углом х к положительному направлению х. Все углы будут приняты положительными при вращении против часовой стрелки от оси, образующей угол χ.

Пусть - α - наклон поверхности массы ледника в положении х, -β - наклон базисного слоя массы ледника в положении х, z₁ - ордината поверхности массы ледника в положении х, z₂ - ордината основания в положении х. Имеем Z = z₁ - z₂ для толщины ледника в положении х и -θ = -α + χ, -φ = -β + χ. Компоненты напряжения в направлении осей х, z обозначим через σ_х, τ_х, σ_z. Рассмотрим массу ледника постоянной плотности ρ.

Пусть g - ускорение силы тяжести. Тогда запишем g_x = +g sinχ, g_z = -g cosχ для его компонентов в направлениях осей.

Уравнения равновесия для медленного постоянного движения ледника тогда могут быть записаны в виде:

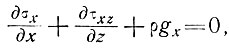
(1)

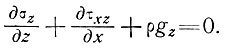
(2)

Эти уравнения справедливы повсюду в массе ледника для любой системы осей, определенной подобным вышеупомянутому образом.

Нам нужно получить выражение для девиатора продольного напряжения 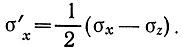. Отсюда дифференцируем выражение (1) относительно оси z и выражение (2) относительно оси х и после вычитания получаем

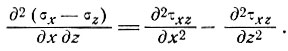
(3)

Это уравнение также не зависит от выбора ориентации оси. Только после интегрирования этого уравнения становится необходимым определить граничные условия в величинах направления оси.

Интегрируем уравнение (3) по оси z от z₁ до z

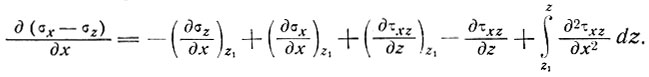
(4)

Решая уравнение (1), получаем, что на поверхности

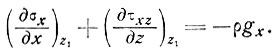
(5)

Отсюда выражение (4) можно записать в виде

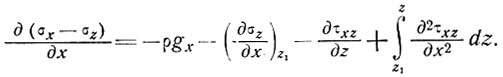
(6)

Теперь, интегрируя вновь по оси z на этот раз от z₁ до z₂ и замечая, что первые два члена правой части уравнения (6) постоянны по оси z, а также, что Z = z₂ - z₁, получаем

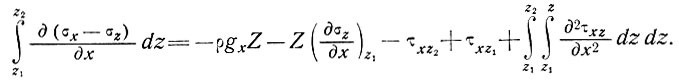
(7)

Это уравнение точное и выражает средний градиент девиатора продольного напряжения в зависимости от граничных условий на поверхности и у основания колонки льда. Исследуем условия на поверхности и у основания колонки льда более подробно. Но сначала требуется проинтегрировать уравнение (7) по направлению оси х. Для этого запишем его левую часть в виде

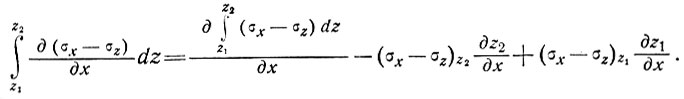
(8)

Граничные условия. Для поверхности ледника принимаем допущение, что напряжение сдвига, параллельное поверхности, равно нулю, и что нормальное напряжение равно атмосферному давлению р.

Если -θ - угол между осью х и поверхностью, то нормальное и сдвиговое напряжения связаны с компонентами в направлениях х и z яа поверхности выражениями:

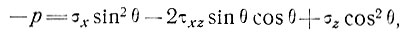
(9)

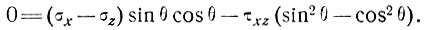
(10)

Для решения уравнения (8) нам нужно лишь иметь выражение (10) в виде (деля на cos²θ)

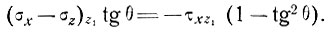
(11)

Аналогично этому у основания, если -τ_б - базисное сдвиговое напряжение, параллельное ложу, где -φ - угол между основанием и осью х

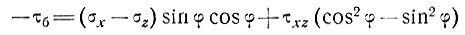
и, таким образом,

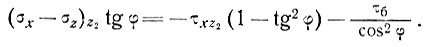
(12)

Поскольку 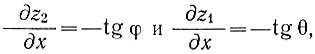используя выражение (11), (12) и подставляя значение формулы (8) в формулу (7), получаем

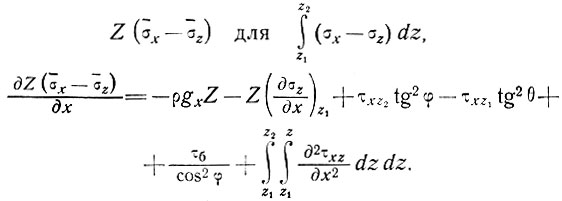
(13)

Член уравнения 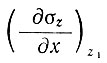равен нулю в тех точках, где поверхность колонки параллельна оси х. Однако при других углах наклона он зависит от продольного напряжения и градиентов напряжения и кривизны поверхности.

Оценим теперь этот член уравнения полностью, чтобы показать, при каких условиях он может аппроксимироваться выражением ρgz tgθ.

Если через s обозначается расстояние вдоль кривизны поверхности, то

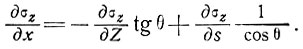
(14)

Пользуясь уравнением (2), выражение (14) можно переписать следующим образом

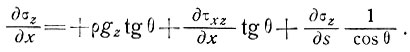
Аналогично, разлагая отношение 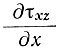и используя уравнение (1), получаем

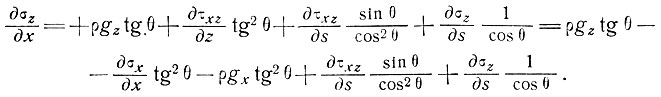
(15)

Если σ_n, σ₁ - нормальное и продольное напряжения и 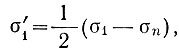то

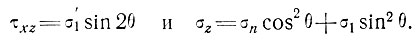
Откуда

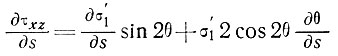
и

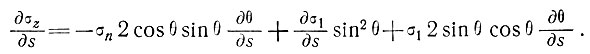
Подставляя эти выражения в уравнение (15) и принимая искомые величины на поверхности, получаем

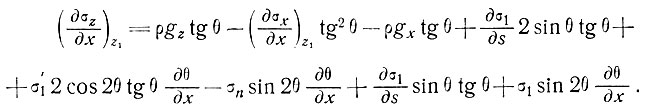
(16)

Теперь, чтобы принять в качестве первого приближения величину

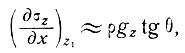
необходимо (и достаточно), чтобы не только наклон θ, но и градиент наклона были малы, т. е. 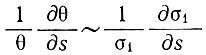- или меньше. Поскольку продольные напряжения изменяются с наклоном поверхности, то обычно это так и бывает. Однако резкие изменения наклона поверхности или напряжения (например, впадины на поверхности) не будут охватываться этой приблизительной формулой.

Наконец, подставляя выражение (16) в уравнение (13) и записывая компоненты полностью, получаем

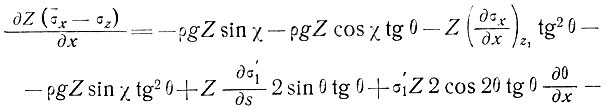
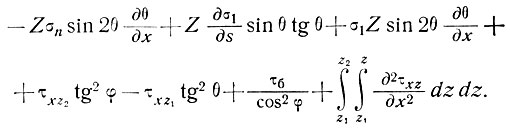
(17)

Это уравнение точное, оно имеет произвольную ориентацию ??? для оси х и справедливо повсюду вдоль массы ледника с такими же прямоугольными координатами, и следовательно, его можно непосредственно интегрировать по оси х, не прибегая к криволинейным координатам. Из этого уравнения можно определить условия, необходимые при решении задач для различных упрощенных случаев.

Специальный случай малого наклона. При малых наклонах χ, θ, φ и градиентах наклона (т. е. пренебрегая вторым и более высокими порядками) все члены, за исключением первых двух и последнего в уравнении (17), пренебрежимо малы, так что оно сводится к виду, полученному Баддом [18],

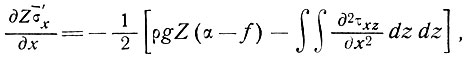
(18)

где 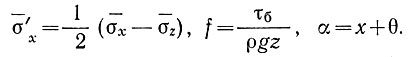В этом случае важен только наклон поверхности, и поэтому безразлично, будут ли оси приняты горизонтальными, параллельными поверхности или параллельными основанию.

Другие упрощенные формы уравнения (17) можно легко получить, выбрав ориентацию горизонтальной оси по следующим направлениям: горизонтально (х = 0) или параллельно поверхности (0 = θ, х = α), или же параллельно основанию (φ = 0, х = β) в каком-либо конкретном положении.