8.3. Профили температуры в ледниковых массах

8.3.1. Влияние нагревания за счет трения на температурный профиль. Температура θ на глубине z в массе ледника толщиной Н в отсутствие аккумуляции или движения определяется температурой на поверхности θ_п. и температурным градиентом в базисном слое γ_б = γ_г (геотермальный теплопоток)

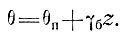
(8)

При горизонтальном движении в зависимости от сдвигового напряжения τ_xz и скорости деформации ε_xz тепло выделяется в результате рассеяния энергии 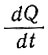от внутреннего трения в виде

(9)

Поскольку скорость деформации зависит от температуры, т. е.

(10)

то рассеяние энергии влияет и на температурные профили, и на профили скорости.

Пренебрегая другими факторами, изменение температуры в базисных слоях определяется уравнением

(11)

где

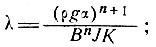
(12)

здесь ρ - плотность льда, g- ускорение силы тяжести, α - наклон в линии движения, J - механический эквивалент тепла и К - теплопроводность льда.

Отсюда изменение температуры можно оценить из решения ряда

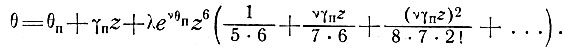
(13)

Установлено, что при таком виде закона течения льда почти 90% тепла в типичной ледниковой массе толщиной 1000 м выделяется в ее нижних 200 м. Поскольку большая часть тепла выделяется в базисных слоях, влияние нагрева за счет трения можно приближенно учесть для большинства ледниковых масс, если принять температурный градиент в базисном слое в виде

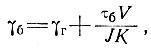
(14)

где V - средняя скорость течения льда в направлении движения ледника и τ_б - напряжение в базисном слое.

8.3.2. Влияние аккумуляции и движения ледника на его профиль температуры. "Робиновский" установившийся профиль температуры для массы ледника в состоянии равновесия при скорости аккумуляции А на поверхности, постоянной температуре на поверхности и пренебрежимо малом горизонтальном переносе массы имеет вид

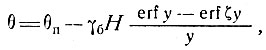
(15)

где

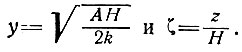
(16)

Температурный градиент на поверхности для этих условий

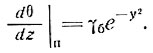
(17)

Влияние горизонтального движения может быть оценено по установившемуся отрицательному температурному градиенту поверхности ледника вследствие его движения вниз по склону и последующего нагревания поверхности в отсутствие теплопроводности:

(18)

где λ - вертикальный средний годовой температурный градиент воздуха.

И наоборот, установившийся профиль температуры ледниковой массы, движущейся наружу и вниз и нагревающейся у поверхности, при наличии достаточной теплопроводности, но при нулевой скорости аккумуляции имеет вид

(19)

с температурным градиентом на поверхности

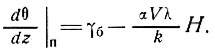
(20)

При наличии как скорости накопления, так и теплопроводности установившийся профиль температуры для колонки ледникового купола, движущейся наружу и вниз в состоянии равновесия и, следовательно, нагревающейся с поверхности со скоростью αVλ, определяется выражением

(21)

где

(22)

При этом поверхностный температурный градиент имеет вид

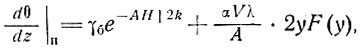
(23)

(23')

т. е. приближенно является суммой правых частей уравнений (17) и (18) или (20).

8.3.3. Температуры в куполовом леднике, изменяющиеся по толщине. Для куполового ледника, в котором по мере движения колонки льда наружу высота Е изменяется с постоянной скоростью 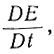, найденный результат аналогичен результату, полученному по уравнению (23). Но в этом случае следует ввести расширяющиеся или сходящиеся координаты движения ледника и нужно использовать в качестве выражения скорости нагревания отношение вместо произведения αVλ, что соответствует установившимся ледниковым массам. В этом случае поверхностный температурный градиент примет вид

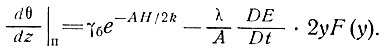
(24)

С помощью этого выражения для тех случаев, когда климатические изменения пренебрежимо малы, можно оценить состояние равновесия или скорость изменения толщины ледника по поверхностному температурному градиенту, толщине ледника и скорости аккумуляции, представленной выражением

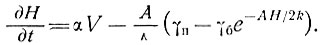
(25)

8.3.4. Неустановившиеся температуры в куполовых ледниках. Если граничные условия не остаются неизменными в течение достаточно долгого времени, то установившиеся профили температуры не реализуются.

Временное отставание t температуры в базисном слое при достижении установившегося состояния можно оценить по уравнению

(26)

где k - скорость постоянного нагревания поверхности при нулевой аккумуляции на поверхности. При аккумуляции на поверхности критерием приближения профиля температуры к устойчивому состоянию будет

(27)

Это условие, по-видимому, реализуется для большинства ледниковых масс, которые находятся в состояний равновесия.

Синусоидальные температурные колебания на поверхности в отсутствие движения или аккумуляции передаются в среду льда со скоростью

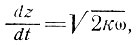
(28)

где ω - частота колебаний.

Длиннопериодные температурные колебания проникают в среду посредством аккумуляции А и движения, перемещаясь вместе со льдом, который на расстоянии z над основанием имеет вертикальную скорость

(29)

Когда обе эти скорости [формулы (28) и (29)] сравнимы, уменьшение амплитуды температурных колебаний с глубиной можно оценить по выражению

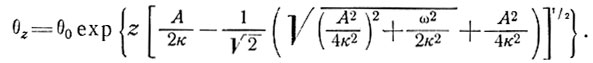
(30)

Расчеты по уравнениям (28) и (29) предполагают, что для куполовых ледников, близких к состоянию равновесия, профили температуры в естественных холодных ледниковых массах будут близки к установившемуся профилю температуры, соответствующему постоянной скорости нагревания на поверхности. Но в тех случаях, когда скорость нагревания быстро возрастает, температуры в базисном слое могут отставать от температур поверхности. Кратковременные температурные изменения быстро затухают в верхних слоях, в то время как долговременные переносятся льдом с уменьшающейся по направлению к основанию скоростью, зависящей от скоростей аккумуляции и деформации.