8.4. Продольный профиль скорости

8.4.1. Глетчеры. Общее уравнение, связывающее продольную скорость на поверхности массы ледника V_п и скорость деформации 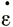вдоль линии тока ледника, т. е. уравнение (25) подраздела 6.2 с поправкой на поперечную деформацию имеет вид

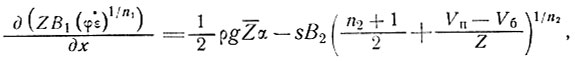
(31)

где φ - коэффициент скорости поперечной деформации, V_б - скорость движения льда в базисном слое, s - коэффициент формы ледника для данного поперечного сечения, зависящий от размеров глетчера, толщины ледника Z, наклона поверхности α и параметров закона течения льда n и В.

Если сглаженная для некоторого расстояния функция, стоящая в левой части уравнения (31), приближается к нулю, то получим связь для сглаженного наклона, скорости и толщины и параметров закона течения, как в уравнении (29) подраздела 6.2

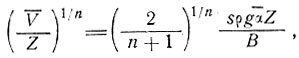
(32)

где параметр В очень сильно зависит от профиля температуры, особенно в донных слоях, и выражается уравнением (37) подраздела 5.1.

Уравнение (32) можно использовать для оценки параметров течения льда, связанных со слоем высокого сдвига у основания, когда профили скорости и толщины известны. И наоборот, если известны параметры течения и профили толщины, то можно оценить продольную скорость.

На продольные деформации, однако, большое влияние оказывают небольшие колебания наклона поверхности по отношению к среднему ее наклону, т. е.

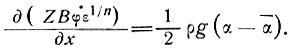
(33)

Измеряя деформации и связанные с ними отклонения наклона поверхности вдоль центральной линии движения ледника, можно оценить параметры течения n и В для всей толщины льда и вообще для значительно более низких сдвиговых напряжений, чем в случае сдвига в базисном слое, рассмотренного выше.

8.4.2. Шельфовые ледники. Общее уравнение скорости движения и скорости деформации вдоль центральной линии движения ледника имеет вид

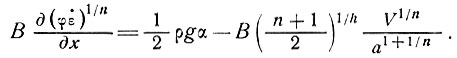
(34)

Для случаев, в которых параметры а, В, n и φ лишь медленно изменяются вдоль линии движения, решение этого общего уравнения можно получить в виде

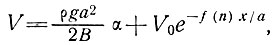
(35)

где

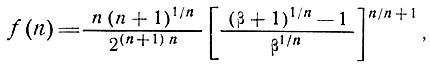
(36)

а β - коэффициент двух членов правой части уравнения (34), т. е. отношение градиента напряжения, являющегося результатом воздействия наклона α, и градиента, обусловленного изменяющейся скоростью ползучести.

Уравнение (35) можно использовать для расчета профиля скорости по размерам шельфового ледника и параметрам течения или для расчета параметров течения по профилю скорости.

8.4.3. Куполовые ледники. Аналогично результатам, полученным для глетчеров, имеем общее уравнение

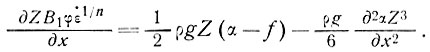
(37)

Последний член правой части уравнения вводится только при коротковолновых колебаниях 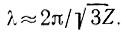. Для сглаженных скоростей, наклона и толщины льда (если среднее значение левой части стремится к нулю), находим

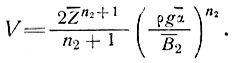
(38)

Уравнение (38) можно использовать для расчета и определения скорости или параметров течения ледника как функций его наклона и толщины.

Параметры n₂ и В₂ в данном случае имеют величины, характерные для слоя льда с большим сдвигом у основания. Для флуктуаций продольной скорости деформации, связанных с отклонениями наклона поверхности от его среднего значения, имеем

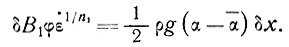
(39)

Это уравнение отражает связь параметров течения льда с его растяжением и сжатием по всему куполовому леднику - при гораздо меньших напряжениях сдвига, чем в базисном слое.

В куполовых ледниках температурная зависимость величин В очень важна. При этом величина В₂ для базисного слоя гораздо ниже по значению (вследствие более высоких температур), чем величина В₁ для массы льда. Более того, существует колебание температуры, а следовательно и параметра В, вдоль линии тока. Это означает, что прежде, чем можно будет получить точные профили скорости, нужно иметь точное представление о профилях температуры ледникового купола.

При волнообразном характере поверхности ледникового купола максимальное растяжение наблюдается на гребнях, а минимумы - над ее впадинами.

8.4.4. Поперечные деформации. Влияние поперечного растяжения 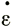_у на профиль продольной скорости заключается в уменьшении скорости продольной деформации 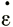_х при данном градиенте наклона поверхности согласно выражению

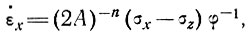
(40)

где

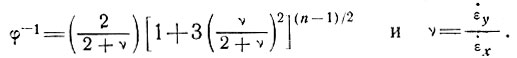
(41)

Это означает, что в общих уравнениях для трехмерного измерения вводится величина φ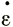^1/_n вместо 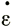^1/_n которая фигурирует в уравнениях для двухмерных измерений, поскольку 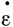_у = 0.

Так как скорости продольной деформации малы, нас вообще интересует здесь та область закона течения льда, для которой n ≈ 1, т. е. мы имеем

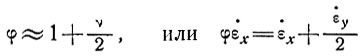
(42)

и видим, что малые деформации, особенно одного знака, оказывают небольшое влияние на продольный профиль. Но в то же время большие боковые деформации такого же порядка, как и продольная (особенно если они противоположны по знаку), могут играть главную роль в процессе деформации. При условии, что дивергенция или конвергенция линий тока известна, влияние боковой деформации можно рассчитать и ввести в уравнения как продольной скорости, так и скорости деформации.

8.4.5. Течение льда по волнообразному ложу. При двухмерном профиле наклона ложа вдоль линий движения ледника вида

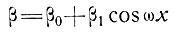
поверхность ледника приобретает установившийся характер, причем ее колебания определяются выражением

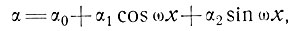
где

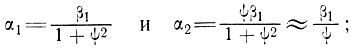
здесь

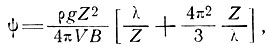
(43)

где Z - толщина льда, V - скорость движения льда, В - параметр вязкости льда, λ = 2π/ω - длина волны колебаний ложа. Коэффициент демпфирования φ минимален при 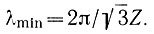. Уравнение (43) можно использовать для определения величин параметра течения В по коэффициенту демпфирования и скорости движения.