
7.5. Траектории движения частиц льда и его возраст
При изучении истории ледника главной задачей является экстраполяция положения каждой частицы льда вдоль пути ее течения вперед или назад во времени. Вообще, по мере опускания или подъема поверхности ледника со скоростью, зависящей от степени дебаланса бюджета его массы, в границе куполового ледника также будут происходить изменения. Это изменение формы ледника вызывает изменение распределения скорости движения, что делает экстраполяцию положений частиц льда во времени очень сложной. Поэтому сначала исследуем пути движения частицы в установившемся ледниковом куполе.
Эта проблема обсуждалась несколькими авторами, в том числе Крэри и другими [26] применительно к шельфовому леднику Росса, Хефели [41] для Гренландии, Мейером [74] для глетчера Саскачеван и Шумским [124 - 126] и Либутри [67] для глетчеров вообще.
Здесь дается обзор этой ранее проделанной работы с точки зрения оценки значимости различных параметров движения частиц вначале для установившегося, а затем неустановившегося состояний ледниковых масс.
7.5.1. Уравнения траекторий. Пусть V - горизонтальная скорость движения элемента льда на расстоянии х от центра ледника во время t на глубине z ниже поверхности. Обозначим скорость аккумуляции в положении х через А, а вертикальную скорость деформации через εz, принимаемую постоянной от поверхности до основания.
Теперь, если нам известны параметры V, εz и А как функции от х, можно определить пути движения частиц льда, т. е. их положения в любой момент времени.
Время δt, необходимое для прохождения частицей льда расстояния δх, равно
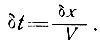
(31)
Отсюда время, необходимое для достижения этой частицей положения х, находится как
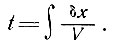
(32)
Аналогично расстояние, пройденное частицей льда за время t, равно
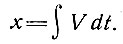
(33)
Увеличение глубины z нахождения частицы ниже поверхности ледника за время δt определяется как
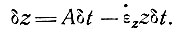
(34)
Откуда
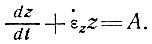
(35)
Крэри [25] показал, что это уравнение имеет следующее решение:
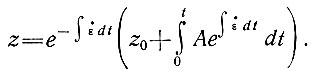
(36)
Если определим
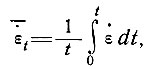
то уравнение (36) примет следующий вид
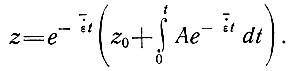
(36')
Можно также выразить эту зависимость переменных от х из уравнения (31), т. е.
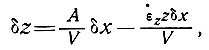
(37)
и
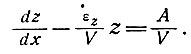
(38)
Откуда
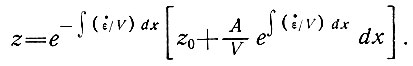
(39)
Пути частиц льда в некоторых случаях можно легче вычислить через их расстояния от основания (скажем, ζ). Если М - скорость таяния в базисном слое, то уравнениями, соответствующими выражениям (37) и (39), будут
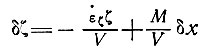
(37')
и
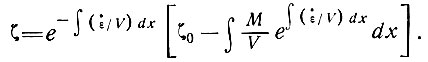
(39')
Поскольку для многих куполовых ледников донное таяние пренебрежимо мало, то это соотношение сводится к виду
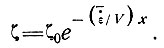
(40)
Результаты расчета траекторий движения частиц льда по этим уравнениям для центральной линии шельфового ледника Эймери и двух профилей куполового ледника Уилкса показаны на рис. 7.4 - 7.6. На этих рисунках представлены изохроны льда, имеющие вид приблизительно параллельных слоев на ледниковом куполе, которые, однако, по мере их приближения к основанию и фронту ледника постепенно сближаются. Можно видеть, что возраст 90% льда куполового ледника Уилкса вдоль профиля купол - мыс Пойнсетт менее 5000 лет.
![Рис. 7.4. Траектории установившегося течения шельфового ледника Эймери, рассчитанные по измеренным скоростям движения и аккумуляции (см. рис. 1.2)[16, 17]. 1 - основание, 2 - траектории течения ледника, 3 - предполагаемое основание 1964 г](pic/000826.jpg)
Рис. 7.4. Траектории установившегося течения шельфового ледника Эймери, рассчитанные по измеренным скоростям движения и аккумуляции (см. рис. 1.2)[16, 17]. 1 - основание, 2 - траектории течения ледника, 3 - предполагаемое основание 1964 г
7.5.2. Влияние различных параметров на траектории движения частиц льда. Хефели [41] теоретически определил установившиеся линии обтекания для центральных областей идеальных ледниковых масс (двухмерных) полосовой и круглой форм, в которых толщина и аккумуляция принимаются постоянными, а ложе плоским. Ниже дается обобщение этого подхода, заключающееся в учете линий тока, искривленных в горизонтальной плоскости, переменной толщины льда, аккумуляции, наклона ложа, а также неустановившегося состояния.
Пусть V - горизонтальная скорость движения частицы льда на расстоянии r от центра ледникового купола и z над ложем в момент времени t. Пусть Vz будет соответствующая вертикальная скорость относительно ложа, которое может быть плоским или нерегулярным.
Площадь между двумя линиями тока масс льда, которые находятся на расстоянии s друг от друга и r от центра ледника, обозначим через Sr. Определим переменный коэффициент λ как
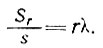
Тогда для частных случаев полосового ледникового щита λ = 1, а для идеального круглого куполового ледника λ = 1/2. Вообще говоря, коэффициент λ является функцией r.
Пусть 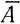 - скорость аккумуляции на расстоянии r от центра и Аr - средняя величина аккумуляции по площади ледника между двумя линиями тока на расстоянии r.
- скорость аккумуляции на расстоянии r от центра и Аr - средняя величина аккумуляции по площади ледника между двумя линиями тока на расстоянии r.
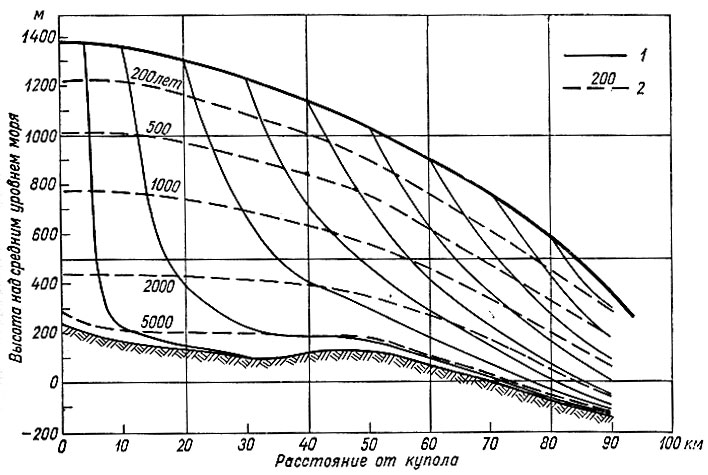
Рис. 7.5. Установившиеся пути движения частиц льда по линии купол - мыс Пойнсетт куполового ледника Уилкса и их изохроны. 1 - пути движения частиц льда, 2 - изохроны
Пусть толщина льда в r будет Н. Тогда уравнение (13) выражает условие неразрывности:
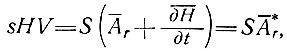
(41)
где 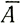 *r - скорость накопления равновесия.
*r - скорость накопления равновесия.
Отсюда горизонтальная скорость движения частиц получается как
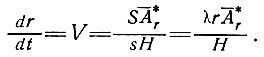
(42)
Вертикальная же скорость движения частиц определяется по уравнению
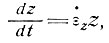
(43)
(43)
где 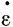 z-скорость вертикальной деформации. Согласно уравнению (9), можно записать
z-скорость вертикальной деформации. Согласно уравнению (9), можно записать
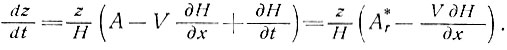
(44)
Следовательно, уравнение линий тока получается по выражениям (42) и (44) в виде
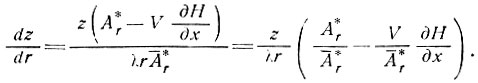
(45)
Откуда
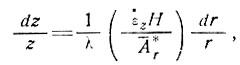
или
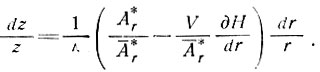
(46)
При условии, что S/s, А, Н, ∂H/∂t известны как функции r, можно рассчитать траектории движения частиц льда, используя ступенчатые приращения δr. Следует отметить, что для неустановившегося состояния масс льда уравнение (46) дает лишь мгновенное положение частиц на траектории. Чтобы проследить пути движения частиц, необходимо знание изменения по времени параметров Н, V и ∂H/∂t, даже если Аr = const. Метод расчета траекторий частиц при неустановившемся состоянии масс льда приведен в последнем разделе. Здесь просто заметим, что неустановившиеся траектории частиц льда получаются использованием скорости аккумуляции в состоянии равновесия А*r и 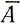 *r, а не фактических величин. Теперь, чтобы исследовать влияние различных параметров, рассмотрим установившееся состояние масс льда, опустив звездочки в уравнении (46).
*r, а не фактических величин. Теперь, чтобы исследовать влияние различных параметров, рассмотрим установившееся состояние масс льда, опустив звездочки в уравнении (46).
1. Дивергенция линий тока. Траектории движения частиц льда [уравнение (46)] сведутся к траекториям движения частиц Хефели, если рассмотрим материковую область куполового ледника, где скорость накопления можно принять постоянной (и отсюда 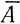 r = Аr), а градиентом толщины пренебречь (
r = Аr), а градиентом толщины пренебречь (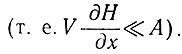 ). Тогда уравнение (46) интегрируется и приводится к виду
). Тогда уравнение (46) интегрируется и приводится к виду
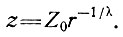
(47)
Это соответствует полосовому щитовому леднику Хефели и круглому щитовому леднику, где λ равно соответственно 1 и 1/2 и z - высота над ложем на расстоянии r, a z = Z0, когда r = 1. В более общем случае λ можно оценить по дивергенции или конвергенции линий тока масс льда. Для круглого куполового ледника относительная дивергенция (по сравнению с радиальной) составляет λ < 1/2, в то время как конвергенция дает λ > 1/2.
2. Переменная аккумуляция вдоль профиля. Влияние изменения скорости аккумуляции вдоль профиля можно исследовать, рассматривая изменения аккумуляции, определяемой зависимостью вида
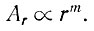
(48)
В этом случае средняя скорость накопления на участке от 0 до r выражается в виде
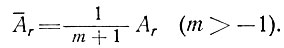
(49)
Затем, принимая λ = 1 и 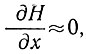 после интегрирования уравнения (46) получим
после интегрирования уравнения (46) получим
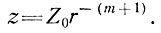
(50)
Таким образом, представляется, что линейное увеличение скорости аккумуляции на некотором расстоянии от центра (m = 1) оказывает такое же влияние на траектории движения частиц льда, как и постоянная круговая дивергенция (λ= 1/2).
Уменьшение величины аккумуляции от центра к краю ледника (m < 0) приводит к относительно медленной сходимости (конвергенции) траекторий движения частиц льда по сравнению со случаем постоянной аккумуляции.
3. Влияние градиента толщины. Из уравнения (46) при постоянных λ и Аr ∝ rm получим
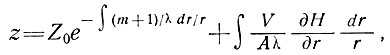
(51)
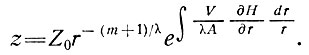
(52)
Отсюда любое уменьшение толщины ледника от центра к краю (∂ Н/∂r отрицательное) приводит к большим скоростям конвергенции траекторий движения частиц в вертикальном профиле. Типичные ледниковые массы уменьшаются по толщине к краю, в то же время скорость их движения обычно возрастает так, что величина 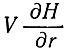 становится большей по сравнению с величиной аккумуляции А. В результате в этой области массы ледника величина градиента толщины, которая может быть рассчитана из уравнения (52), столь же важна при определении траектории движения частиц льда, что и скорость аккумуляции.
становится большей по сравнению с величиной аккумуляции А. В результате в этой области массы ледника величина градиента толщины, которая может быть рассчитана из уравнения (52), столь же важна при определении траектории движения частиц льда, что и скорость аккумуляции.
7.5.3. Траектории неустановившегося состояния. Чтобы проследить пути движения частиц льда в массе ледника, не находящегося в установившемся состоянии, необходимо сначала рассчитать изменение δН толщины поверхности ледника за время δt по выражению
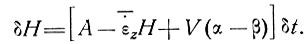
(53)
Это позволит установить новый профиль высоты ледника. После этого все еще сохраняется возможность отнести глубину к полученной поверхности и воспользоваться уравнениями (37) и (39), чтобы рассчитать положение частицы льда на первом этапе движения.
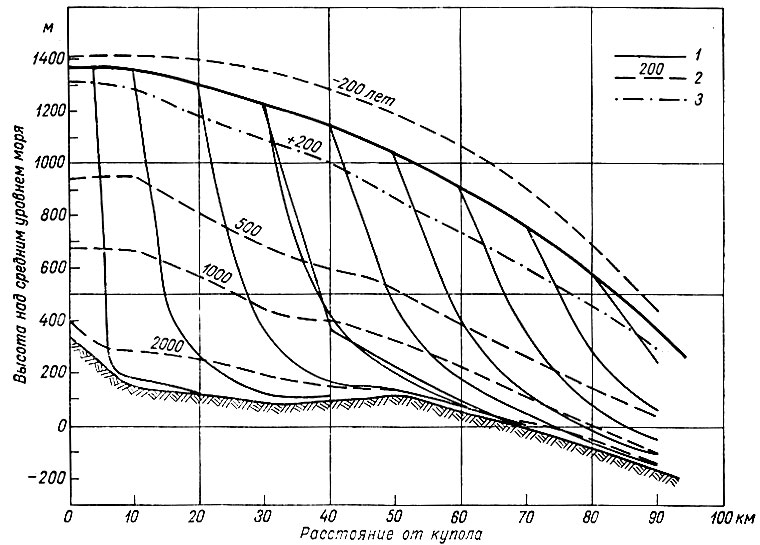
Рис. 7.7. Неустановившиеся пути движения частиц льда по линии между сетками напряжения D и J куполового ледника Уилкса. 1 - пути движения частиц льда, 2 - изохроны, 3 - изохрона будущего состояния ледника
По мере изменения толщины ледника изменяются и его наклон и скорость движения. Отсюда из выражения для скорости
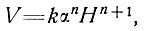
(54)
где
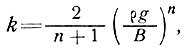
можно получить величину ее изменения при условии, что температуры (и, следовательно, параметр В) остаются теми же, т. е.
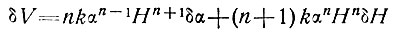
(55)
или
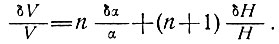
(56)
Теперь при новом профиле скорости движения ледника на следующей временной ступени можно рассчитать положение частицы льда. При этом отношение 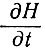 изменится с изменением величины параметров V и Н и в некоторых случаях может стремиться к нулю, приводя к устойчивому состоянию ледник. Но, вообще говоря, устойчивое состояние не достигается, и, таким образом, вышеприведенная методика экстраполяции должна использоваться и далее.
изменится с изменением величины параметров V и Н и в некоторых случаях может стремиться к нулю, приводя к устойчивому состоянию ледник. Но, вообще говоря, устойчивое состояние не достигается, и, таким образом, вышеприведенная методика экстраполяции должна использоваться и далее.
Этот процесс при длительной экстраполяции становится очень утомительным, но благодаря наличию обратной связи к нему применимы итерационные методы вычислительной техники. Однако заметим, что скорость аккумуляции и параметры течения льда считались постоянными. При длительной экстраполяции и при больших изменениях в размерах куполовых ледников такая аппроксимация не годится. Таким образом, без подробной информации об изменении аккумуляции и температуры (а отсюда и параметров течения массы ледника) за большой период времени продолжительные расчеты по исследованию образования или разрушения больших ледниковых масс являются преждевременными.
В качестве примера использования итерационного метода на рис. 7.7 представлены результаты сравнительно краткосрочной экстраполяции неустановившегося состояния ледника, которые позволяют определить положения поверхности куполового ледника Уилкса несколько сотен лет назад, а также через такой же период в будущем.
|
ПОИСК:
|
© GEOMAN.RU, 2001-2021
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'