
7.4. Профили высоты поверхности куполового ледника
Как было установлено в разделе 6, профиль скорости от центра к краю куполового ледника определяется в большой степени толщиной ледника, наклоном поверхности и параметрами течения льда. Выше мы видели, что при определенных величинах параметров V, Н, А, α, β поверхность ледникового купола оставалась стационарной во времени. Если аккумуляция слишком велика, чтобы равновесие могло установиться, то толщина ледникового купола возрастает. Это приводит к увеличению скорости движения ледника и растекания, таким образом на некотором этапе все же может быть достигнуто состояние равновесия.
Рассмотрим теперь форму профиля ледникового купола в стационарном состоянии. Этим вопросом занимались многие исследователи, включая Ная [89, 90], Вертмана [141, 142, 145, 146], Хефели [40], Шумского [124 - 126], Либутри [65]. Проводимый ниже анализ аналогичен анализу Хефели, поскольку закон зависимости скорости движения от наклона и толщины ледника, используемый здесь, аналогичен закону, которым пользовался Хефели, за исключением того, что в нашем случае учитывается изменение параметра течения β с изменением температуры.
Для случая когда градиент продольной скорости деформации по толщине ледника мал,
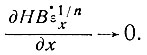
Между скоростью V, толщиной льда Н и наклоном поверхности α и параметрами закона течения n и В существует простое степенное соотношение, а именно уравнение (40) раздела 5:
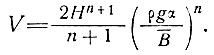
(18)
Теперь при состоянии равновесия уравнение (2б') дает следующую связь между скоростью движения, толщиной льда и скоростью аккумуляции (для куполового ледника с постоянным углом дивергенции):
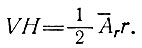
Отсюда, уравнивая эти две скорости, получаем для профиля высоты поверхности куполового ледника при состоянии равновесия (опуская индекс r)
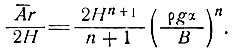
(19)
При нулевой дивергенции аналогичное уравнение имеет вид
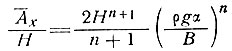
что соответствует уравнению (19), но при двойной скорости аккумуляции. Ниже показано, что это приводит лишь к небольшому различию по форме.
Для более общего случая куполового ледника - при изменяющемся угле дивергенции линий тока - соответствующее отношение можно получить, используя уравнение (2'), в виде
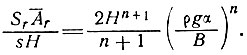
(19')
7.4.1. Влияние наклона ложа. Мы видим, что уравнение
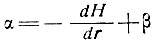
(20)
связывает наклон поверхности ледника с градиентом его толщины и наклоном ложа.
Отсюда, из уравнений (19) и (20) получаем
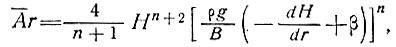
(21)
или
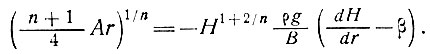
Наклон ложа можно выразить как -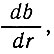 , где b - высота ложа.
, где b - высота ложа.
Уравнение (21) можно проинтегрировать, допустив при этом, что А и В - константы:
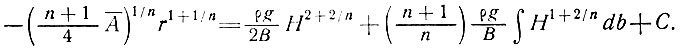
(22)
Во многих случаях высота ложа b мала по сравнению с толщиной ледника Н, и поэтому ею можно пренебречь. Вообще, это уравнение можно проинтегрировать численно, используя особенности функций b (r) и Н(r), как указывалось Наем [89, 90].
Чтобы получить представление об общем влиянии ложа на установившийся профиль поверхности ледника, рассмотрим частный случай, когда высота ложа повсюду составляет некоторую постоянную небольшую часть v толщины ледника.
Тогда db = νdH и из уравнения (22) имеем
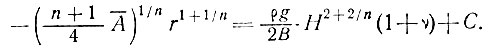
(23)
В этом случае основная "форма" поверхности ледника остается неизменной, а поскольку величина v обычно менее чем 25%, установившийся профиль поверхности ледника подвергается лишь небольшому изменению. Влияние ложа "в чистом виде" эквивалентно случаю, когда имеем меньшую величину параметра В, выражаемую как
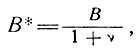
Более того, из уравнения (23) как ответ на вопросы 1 и 2 подраздела 7.1 следует, что при заданных постоянных условиях (аккумуляции А и параметрах закона течения n и В) образуется установившийся профиль поверхности куполового ледника, но этот профиль не однозначен, поскольку граничная величина С определяется отношением Н/r. Отсюда, чтобы этот профиль был однозначным, следует ввести параметр r0. Практически этот параметр обычно определяется такими внешними факторами, как высота ложа, воздействие морской воды, температура воздуха и скорость абляции.
Из уравнений (10) и (18) имеем
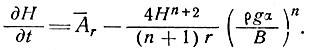
(24)
Этот результат показывает, если значения Аr или В отклоняются от равновесных величин, то толщина ледника изменится таким образом, что все же будет наблюдаться тенденция к установившемуся состоянию. Однако существуют возможности неравного распределения величин А и ∂H/∂t, которое могло бы вызвать волны, выбросы и колебания с задержками по фазе и последующими "поисками" без достижения равновесия более чем на короткий момент времени.
Исследуем теперь более детально профиль высоты поверхности куполового ледника на плоском основании, т. е. при β=0. Если запишем r = r0, когда Н = 0, и Н = Н0, когда r = 0, то сможем представить уравнение (23) в виде
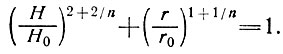
(25)
Это и есть уравнение, выведенное Хефели [40], и оно отличается от уравнения Ная [89, 90], а именно
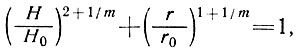
(26)
экспонентой 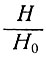 (т. е. 2+1 /m по сравнению с 2 + 2/n). Параметр m Ная является экспонентой принятого отношения между напряжением τ и скоростью V вида
(т. е. 2+1 /m по сравнению с 2 + 2/n). Параметр m Ная является экспонентой принятого отношения между напряжением τ и скоростью V вида
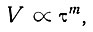
где 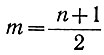 для скольжения, т. е. при n, равном 1, 2, 3, 4, и m равном 1, 1,5, 2, 2,5.
для скольжения, т. е. при n, равном 1, 2, 3, 4, и m равном 1, 1,5, 2, 2,5.
Отсюда видим, что при n ≈ 3 или 4 профили Хефели [уравнение (25)] и Ная [уравнение (26)] отличаются не очень существенно. Най [89, 90] показал, что профиль (26) стремится к параболе, по мере того как m→∞ (случай идеальной пластичности). Это справедливо также и для профиля (25).
7.4.2. Влияние параметра течения льда В. Вообще, параметр течения В меняется с температурой. Можно ожидать, что средняя температура θ по куполовому леднику будет уменьшаться с возрастанием высоты его поверхности. Таким образом, если бы величина параметра 5, типичная для данной массы ледника, зависела от средней температуры по леднику, то можно было бы ожидать, что значение параметра В увеличивается с величиной Я. В этом случае при анализе уравнения (21) можно видеть, что если
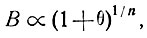
как в расчетах Шумского [122, 123], и если
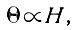
то
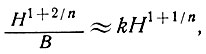
где k = const. Профиль (25) тогда сводится к профилю Ная при m, замененном на n.
Однако поскольку большая часть сдвига происходит в базисных слоях, для определения величины параметра В весьма существенную роль играет температура в этих слоях, а не средняя температура по всему леднику. Из результатов анализа температуры в куполовых ледниках (раздел 4) явствует, что температуры в базисном слое могут уменьшаться по мере движения в глубь материка и зависят от характера аккумуляции, толщины ледника, скорости и т. д. Поэтому подробный общий анализ влияния температуры на профили высоты поверхности куполового ледника требует очень много места, чтобы его можно было включить в настоящее исследование.
Как следствие рассмотрения уравнений (23) и (25) получаем уравнение, связывающее максимальную высоту поверхности ледника Н0, его ширину, r0, скорость аккумуляции А и параметры течения n и В (принимаемые здесь постоянными),
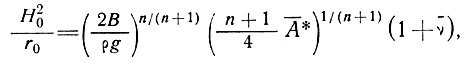
(27)
где при состоянии равновесия 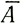 *=
*=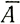 , а в его отсутствии
, а в его отсутствии 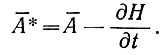
Отсюда получаем оценку величины параметра В в виде
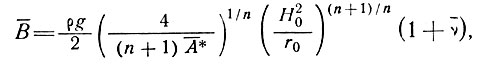
(28)
и, следовательно, если известна величина параметра я, по размерам массы ледника и скорости накопления можно оценить значение В.
Величину параметра n можно сначала определить из закона, выражающего зависимость скорости движения от наклона поверхности и толщины ледника [уравнение (18)] при условии, что профиль скорости нам известен.
Можно видеть, что значение параметра В (если оно постоянно по региону) влияет лишь на размер, а не на форму ледника. Форма в этом случае определяется прежде всего параметром n. Хефели [40] приводит соответствующие уравнения (25) для нескольких значений параметра n и показывает, как различные ледниковые массы сравниваются при этих значениях. Этот результат предполагает, что соответствующие величины параметра n лежат между 3 и 4, как было установлено для куполового ледника Уилкса.
Если параметр В не константа и известен как функция r, уравнение (21) может быть записано в виде
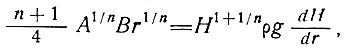
и после интегрирования этого выражения можно определить новую форму ледника. В табл. 7.2 показаны расчетные средние величины 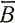 по уравнению (28) для нескольких профилей куполовых ледников. Для куполового ледника о. Рузвельта и Гренландии было принято допущение о нулевой дивергенции, в то время как для остальных куполовых ледников принималась идеальная круговая дивергенция.
по уравнению (28) для нескольких профилей куполовых ледников. Для куполового ледника о. Рузвельта и Гренландии было принято допущение о нулевой дивергенции, в то время как для остальных куполовых ледников принималась идеальная круговая дивергенция.
Величины аккумуляции, приведенные для куполового ледника Уилкса, представляют равновесную аккумуляцию 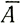 *. Для других куполовых ледников использовалась фактическая аккумуляция. Если бы Гренландия опускалась, а Антарктида поднималась, то использование величин равновесной аккумуляции привело бы к сближению значений этих величин. Погрешности в определении величины параметра В составляют примерно ±0,2 · 109, и поэтому делается вывод, что эффективные средние величины В различаются не более чем на эту рассчитанную погрешность для различных куполовых ледников. Это означает, что рассчитанные величины В не достаточно точны, чтобы обеспечивать разрешение различных средних температур в базисном слое для куполовых ледников. Величины В, установленные для куполового ледника Уилкса, близки к аналогичным величинам, полученным по профилям толщина - скорость - наклон по уравнению (18) [0,85 × 109 дин/(см2 · с1/3)], и указывают на среднюю температуру в базисном слое около -10°С (см. п. 6.3.1). Для более точного анализа следует учитывать изменение высоты ложа в соответствии с уравнением (22).
*. Для других куполовых ледников использовалась фактическая аккумуляция. Если бы Гренландия опускалась, а Антарктида поднималась, то использование величин равновесной аккумуляции привело бы к сближению значений этих величин. Погрешности в определении величины параметра В составляют примерно ±0,2 · 109, и поэтому делается вывод, что эффективные средние величины В различаются не более чем на эту рассчитанную погрешность для различных куполовых ледников. Это означает, что рассчитанные величины В не достаточно точны, чтобы обеспечивать разрешение различных средних температур в базисном слое для куполовых ледников. Величины В, установленные для куполового ледника Уилкса, близки к аналогичным величинам, полученным по профилям толщина - скорость - наклон по уравнению (18) [0,85 × 109 дин/(см2 · с1/3)], и указывают на среднюю температуру в базисном слое около -10°С (см. п. 6.3.1). Для более точного анализа следует учитывать изменение высоты ложа в соответствии с уравнением (22).
Таблица 7.2
Параметр течения 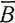 для установившихся профилей куполового ледника
для установившихся профилей куполового ледника
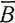 для установившихся профилей куполового ледника
для установившихся профилей куполового ледника| Куполового ледника | r0, км | Н0, м | А, г/см2 | ν | В, дин/(см2 · с1/3) | Примечание | Автор |
| Дригальского I | 10 | 426 | 70 | 0,05 | 0,75 · 109 | В среднем весь остров | Бакаев [4] |
| Рузвельта I | 40 | 760 | 20 | 0,10 | 0,71 · 109 | Центральный сектор Е - W | Клапп [24] |
| Уилкса (а) | 96 | 1200 | (100) | 0,20 | 0,75 · 109 | От купола до мыса Пойнстнетт | Макларен [71] |
| Уилкса (b) | 115 | 1200 | (30) | 0,42 | 0,75 · 109 | От купола до мыса Фольгера | Макларен [71] |
| Гренландия | 560 | 3200 | 45 | 0 | 0,73 · 109 | Профиль EGIG | Бадер [3] |
| Антарктида | 1200 | 3700 | 15 | 0 | 0,68 · 109 | Вглубь от станций Уилкса и Мирный | Бакаев [4], Батти [6] |
Из уравнения (27) очевидно, что при всех остальных постоянных параметрах изменение максимальной толщины льда со средней величиной параметра течения В определяется по формуле
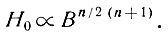
или при n = 3
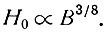
7.4.3. Влияние аккумуляции. Допуская, что величины аккумуляции по всей площади куполового ледника и параметры его течения постоянны, из уравнений (24) и (25) видим, как общий размер куполового ледника в установившемся состоянии зависит от величины аккумуляции. Фактическая форма ледника зависит лишь от величины параметра n (или изменения различных параметров в зависимости от параметра r), но отношение максимальной высоты ледника к его ширине зависит от скорости аккумуляции. Из уравнения (27) видим, что для данного радиуса r0 максимальная толщина пропорциональна 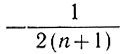 - той степени аккумуляции, т. е.
- той степени аккумуляции, т. е.
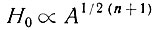
или при n = 3
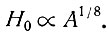
При тех же размерах ледника и параметрах течения и при n = 3 прямоугольный куполовый ледник (с нулевой дивергенцией) в 21/8 · 1,04 раз выше, чем соответствующий круглый ледниковый купол.
К аналогичному выводу, применительно к скорости аккумуляции, выраженной законом течения льда малой степени, пришел и Най [89, 90]. Как указывал Хефели, следствием этого общего отношения является то, что скорость аккумуляции оказывает лишь малое влияние на максимальную высоту массы ледника. Однако этот вывод справедлив лишь до тех пор, пока радиус r0 остается постоянным. Если бы скорость аккумуляции возросла, то масса ледника расширилась бы вообще и увеличилась по толщине. В действительности же предел размера массы ледника чаще может определяться топографией базисного слоя, морской водой и доминирующими температурами.
При постоянной высоте в центре ледника и постоянных параметрах его течения размеры ледника связаны со скоростью аккумуляции следующим образом:
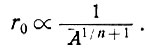
В качестве конкретного примера отметим различные размеры r1 и r2 для куполового ледника Уилкса на его сторонах с различными скоростями накопления (А1 для линии купол - мыс Пойнсетт и A2 для линии купол - мыс Фольгера), показанные в табл. 7.2. Хотя A1 = 0,3A2, результирующие величины параметра В отличаются незначительно. Согласно уравнениям (7), (76) и (27), в случае нулевой дивергенции очевидно, что размер идеального круглого куполового ледника равен 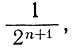 или ≈ 1,9 при n = 3, умноженному на размер соответствующей прямоугольной или двухмерной модели. Для областей с конвергенцией уменьшение размеров еще более выражено.
или ≈ 1,9 при n = 3, умноженному на размер соответствующей прямоугольной или двухмерной модели. Для областей с конвергенцией уменьшение размеров еще более выражено.
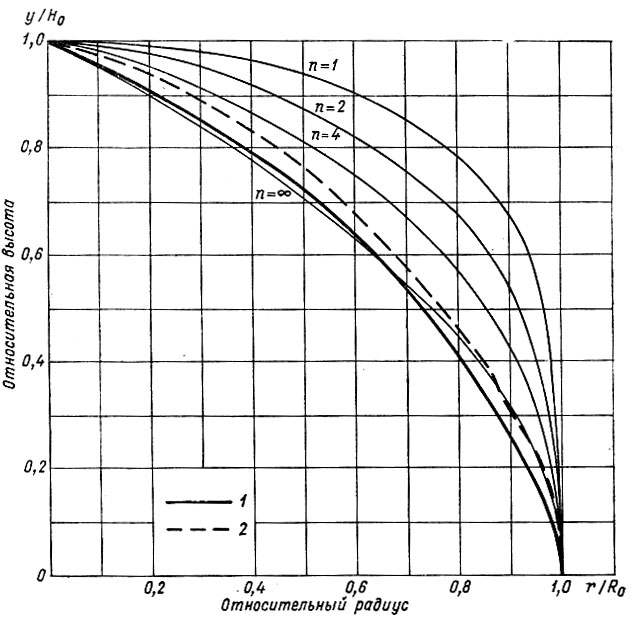
Рис. 7.3а. Профили относительной высоты у/Н куполового ледника Уилкса. 1 - купол - мыс Фольгер, 2 - купол - мыс Пойнсетт
Еще один момент, отмеченный Хефели, заключается в том, что, чем крупнее масса ледника, тем меньше отношение толщины ледника к его радиусу (при условии, что остальные параметры одинаковые). В табл. 7.3. приведены величины среднего радиуса R0 и максимальной толщины ледника Н0 (над нулевой точкой ложа) и отношения H0/R0 и H20/R0 для ряда куполовых ледников.
Данные табл. 7.3 подтверждают качественный прогноз Хефели и, более того, показывают, что отношение H20/R0 остается удивительно стабильным и что часть остаточного изменения отношения Н20/R0 является следствием различных скоростей аккумуляции и дивергенции.
Таблица 7.3
Относительные размеры различных ледниковых куполов
| Куполового ледника | R0, км | Н0, м | Н0/R0 | Н20/R0 |
| Дригальского | 10 | 426 | 5,30 · 102 | 1,80 |
| Рузвельта | 40 | 760 | 1,90 | 1,40 |
| Уилкса | 115 | 1200 | 0,96 | 1,26 |
| Гренландия | 560 | 3200 | 0,17 | 1,35 |
| Антарктида | 1200 | 3700 | 0,03 | 1,15 |
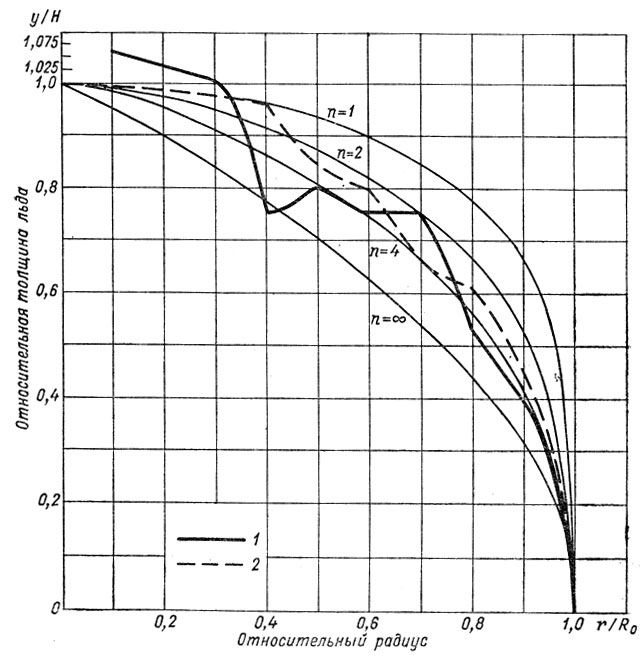
Рис. 7.36. Профиль относительной толщины льда у/Н куполового ледника Уилкса. 1 - купол - мыс Фольгер, 2 - купол - мыс Пойнсетт
Вообще, случаи, когда скорость аккумуляции от центра до края постоянна - необычны. Однако если мы знаем величину А(r) как функцию от значений r, то уравнение (21) можно легко проинтегрировать, чтобы получить соответствующий установившийся профиль.
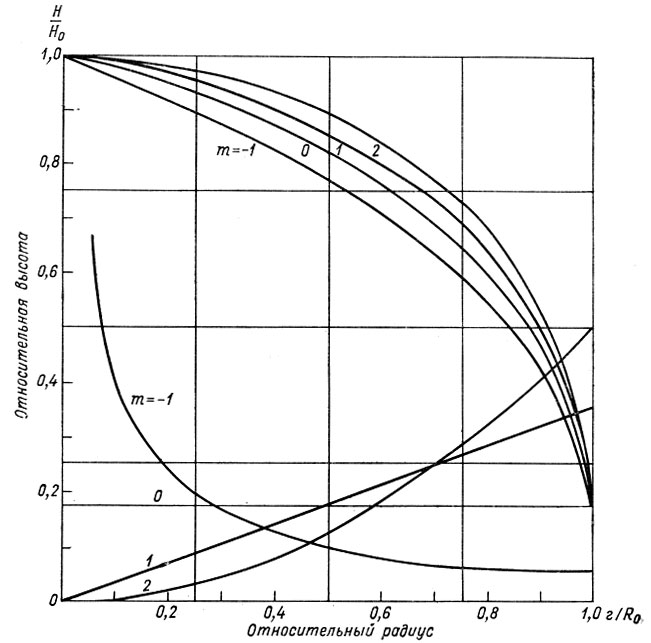
Рис. 7.3в. Влияние формы профиля аккумуляции на форму установившегося состояния куполового ледника для четырех типов профилей накопления А ∝ rm для профиля куполового ледника при постоянном степенном законе течения В и n = 3
В качестве примера предположим, что 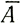 (r) =аrm где а и m - константы, и, кроме того, пусть в данный момент β ≈ 0, В - константа. Тогда уравнение (21) сводится к
(r) =аrm где а и m - константы, и, кроме того, пусть в данный момент β ≈ 0, В - константа. Тогда уравнение (21) сводится к
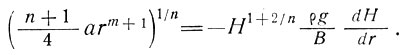
(29),
Интегрируя, получаем, так же как и раньше,
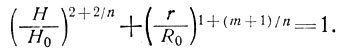
(30)
Отсюда следует, что, хотя величина постоянной скорости аккумуляции по площади не влияет на форму профиля, на нее влияет характер аккумуляции. На рис. 7.3в показано, как различные типичные характеры скорости аккумуляции влияют на установившуюся форму массы ледника.
|
ПОИСК:
|
© GEOMAN.RU, 2001-2021
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'