
7.3. Аномалия бюджета и его изменение
В общем случае для массы ледника, в которой аккумуляция не везде уравновешивает изменение массы ледника вследствие его движения, в итоге будет наблюдаться чистое изменение формы ледника (при данных изменениях формы ледника по высоте или толщине, или контуров во времени). Чистое изменение формы ледника по его толщине во времени 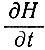 над фиксированной точкой ложа зависит от скорости аккумуляции Л, скорости таяния в базисном слое М, толщины льда Н и средней скорости вертикальной деформации
над фиксированной точкой ложа зависит от скорости аккумуляции Л, скорости таяния в базисном слое М, толщины льда Н и средней скорости вертикальной деформации 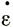 z = (
z = (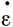 x +
x + 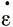 y), горизонтальной скорости V и наклонов поверхности α и базисного слоя β в соответствии с отношением
y), горизонтальной скорости V и наклонов поверхности α и базисного слоя β в соответствии с отношением
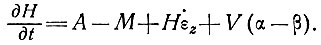
(9)
Все члены этого уравнения имеют размерность в сантиметрах слоя льда в год. При этом мы пренебрегаем изменением плотности в поверхностных слоях массы ледника.
Если все параметры правой части уравнения (9) для куполового ледника известны, то можно рассчитать величину изменения формы этого ледника. Изменение толщины со временем также можно найти, обобщая формулы (7) и (8):
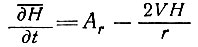
(10)
или
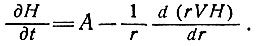
(11)
Последняя - для круглого куполового ледника с постоянным углом дивергенции.
Для более общего случая из формулы (1) получим
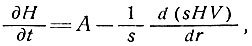
(12)
а для средней скорости понижения поверхности 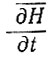 по всей площади S между линиями тока имеем
по всей площади S между линиями тока имеем
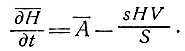
(13)
С помощью уравнений (11) и (13) можно рассчитать величину понижения поверхности в каждой точке поверхности куполового ледника, где известны скорость аккумуляции, толщина ледника и скорость. С помощью уравнений (10) и (12) можно найти величину среднего понижения поверхности по участку ледника, которая должна согласоваться с аналогичной величиной, полученной по уравнению (9), что даст возможность таким образом проверить точность и обоснованность метода.
Результаты этих расчетов, проделанных Л. Пфитцнером для куполового ледника Уилкса, показаны на рис. 7.2. По этому рисунку можно видеть, что ледник не находится в стационарном состоянии. Западная его сторона остается довольно стационарной, а северо-восточная быстро понижается, изменяя таким образом форму куполового ледника. Эта часть ледника ниже, чем другие, находящиеся на том же расстоянии от центра. Обратная экстраполяция по времени дает основание предполагать, что если теперешняя скорость изменения формы ледника была постоянной, то около 400 лет назад ледниковый купол был близок к симметричному.
Непосредственную проверку состояния изменения массы какого-либо ледника можно осуществить точными измерениями профиля высоты и скорости изменения этого профиля во времени. Обычно для определения высоты или скорости изменения высоты массы ледника пользуются нижеследующими методами.
1. Точная оптическая нивелировка поверхности куполовых ледников позволяет определить ее высоты в пределах десятков сантиметров на расстоянии свыше 100 км. Это обычно трудоемкий и медленный процесс, тем более что для обнаружения вертикальных изменений нужно затем снова повторить нивелировку по всей линии. Например, 100-километровый оптический нивелировочный профиль был получен Пфитцнером в 1966 г. На обратном пути было установлено, что погрешность не превышала ±30 см.
2. Неоднократная воздушная фотограмметрия. При условии достаточного наземного контроля и одновременно наличия на поверхности массы ледника соответствующих маркеров и хорошо выраженных особенностей с помощью современных высококачественных камер и устройств топографической съемки при вертикальном определении высоты можно добиться точности 1 м или еще лучше [12, 52, 56].
![Рис. 7.2. Годовые скорости чистого понижения поверхности куполового ледника Уилкса, полученные в результате расчетов дивергенции потока с использованием величин измеренных скоростей движения, деформаций и аккумуляции [103]. Буквы - сетки деформаций. 1 - высота, м, 2 - скорость чистого понижения поверхности, м/год](pic/000758.jpg)
Рис. 7.2. Годовые скорости чистого понижения поверхности куполового ледника Уилкса, полученные в результате расчетов дивергенции потока с использованием величин измеренных скоростей движения, деформаций и аккумуляции [103]. Буквы - сетки деформаций. 1 - высота, м, 2 - скорость чистого понижения поверхности, м/год
3. По неоднократным гравитационным измерениям по маркерам на поверхности ледника можно определить изменение ее высоты. В идеальном случае повторные измерения должны проводиться над одной и той же точкой ложа. Если горизонтальное перемещение ледника мало по сравнению с его толщиной, тогда изменение силы тяжести Δg около маркера на поверхности зависит лишь от понижения ΔЕ и изменения толщины ледника ΔН. Если допустить, что профиль плотности льда остается постоянным, то имеем
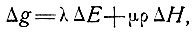
(14)
где λ - изменение силы тяжести с высотой (≈ -0,31 мгал/м) [27], ρ - удельный вес льда (≈ 0,917), μ - коэффициент притяжения бесконечной глыбы единичной толщины и единичной разности плотности (≈ 0,042 мгал/м).
В случае понижающегося или повышающегося уровня куполового ледника, повторяющего движение точки на поверхности колонки льда, где скорость аккумуляции А, скорость таяния в базисном слое М, толщина льда Н, средняя скорость вертикальной деформации 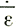 z, скорость движения V и наклон основания β, изменение высоты со временем Δt определяется из выражения
z, скорость движения V и наклон основания β, изменение высоты со временем Δt определяется из выражения
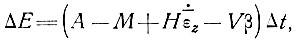
(15)
а изменение толщины льда равно
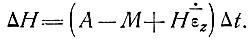
(16)
Отсюда для изменений силы тяжести Δg получаем
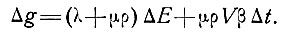
Тогда
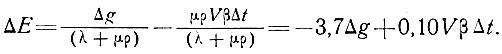
(17)
Изменение толщины льда над определенной точкой ложа определяется по выражению
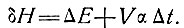
В табл. 7.1 показаны предварительные измерения силы тяжести, проведенные Д. Картером в 1967 г., в определенных точках сетки деформации на ледниковом куполе Уилкса, а также расчетные изменения его высоты. В таблице показаны также изменения высоты этого ледника, рассчитанные Л. Пфитцнером по результатам измерений деформации, скорости движения, толщины льда, наклона и скоростей аккумуляции для каждой сетки деформации и поверхности колонки льда, движущейся вместе с маркером вниз по леднику.
Таблица 7.1
Скорость понижения поверхности куполового ледника, рассчитанная по результатам измерения гравитации g и дивергенции потока f, м/год
| Сетка деформации | А | В | С | D | G | H | J | K | L |
| f. . . . . . . . . . . . . . . . | 0,4 | 0,5 | 0,5 | 1,5 | 2,0 | 2,4 | (5) | 0,4 | 0,6 |
| g. . . . . . . . . . . . . . . . | 0,5 | 0,6 | 0,6 | 1,3 | 1,3 | 2,2 | 3,0 | 1,5 | 0,9 |
Можно видеть, что скорость понижения поверхности, рассчитанная по результатам гравитационных измерений, несмотря на все еще большие погрешности измерений на этом этапе, хорошо согласуется с данными, полученными по результатам расчета дивергенции потока. Точные измерения такого рода можно использовать, чтобы установить разницу между 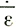 z - средней скоростью деформации по леднику и
z - средней скоростью деформации по леднику и 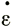 z - скоростью деформации на поверхности. Поскольку из разделов 5 и 6 следует, что скорость деформации может иметь в значительной степени локальный характер, важно получить ее значения, осредненные по регионам, имеющим значительные площади, а не величины, измеренные в отдельных точках.
z - скоростью деформации на поверхности. Поскольку из разделов 5 и 6 следует, что скорость деформации может иметь в значительной степени локальный характер, важно получить ее значения, осредненные по регионам, имеющим значительные площади, а не величины, измеренные в отдельных точках.
|
ПОИСК:
|
© GEOMAN.RU, 2001-2021
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'