7.2. Условия состояния равновесия

Рассмотрим обобщенный сектор куполового ледника между двумя линиями тока льда, которые находятся на небольшом расстоянии s друг от друга и расстоянии r от центра (рис. 7.1).

Пусть V будет средняя скорость в направлении вперед в положении r, где толщина льда Н и скорость аккумуляции А.

Тогда условие состояния равновесия будет в том, что течение льда по площади sH равно аккумуляции на этой площади между линиями тока в глубь материка от этого сектора на расстоянии r, т. е.

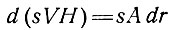
(1)

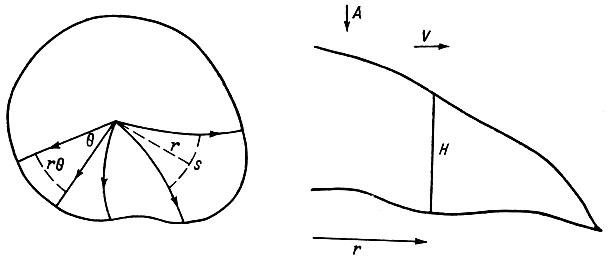
Рис. 7.1

или

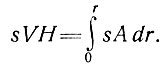
(2)

Теперь определим 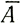_r как среднюю скорость аккумуляции в секторе между линиями тока от центра на расстоянии r:

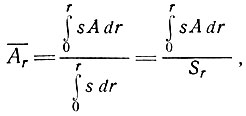
(3)

где S_r - площадь между линиями тока на расстоянии r. Тогда уравнение (2) можно записать в виде

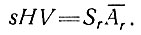
(2')

Для специального случая, когда угол дивергенции θ линий тока льда постоянный, имеем уравнения:

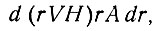
(1б)

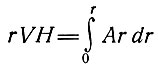
(26)

и

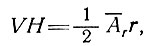
(2б')

где

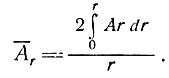
(3б)

Когда угол дивергенции θ равен нулю, полученный результат сводится к аналогичному результату для двух измерений или цилиндрического поперечного сечения, т. е.

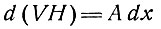
(1в)

или

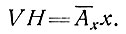
(2в')

Здесь

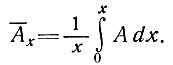
(3в)

Для рассмотренного куполового ледника с постоянным углом дивергенции скорость равновесия получается из уравнения (2б') как

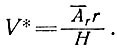
(4)

Для случая нулевой дивергенции скорость равновесия, соответствующая аналогичной в уравнении (4), выражается через

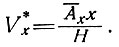
(4в)

Дифференцируя (4), получаем скорость продольной деформации равновесия, выражаемую (опуская индекс r у 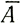) как

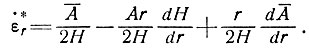
(5)

Скорость деформации можно выразить и в значениях скорости V из уравнения (1) в виде

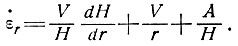
(6)

Эти уравнения можно использовать, чтобы ответить на вопросы 2 и 3, подраздела 7.1. В частности, они позволяют вывести величину требуемых скоростей движения и деформации для состояния равновесия массы ледника по данным профилям толщины и аккумуляции вдоль линии тока ледника. Если, кроме того, будут измерены скорости движения и деформации, то можно провести проверку состояния равновесия массы ледника вдоль линий тока.

В том случае, когда состояние равновесия массы ледника не устанавливается, можно считать, что уравнение (2б') определяет требуемый профиль аккумуляции А* и уравновешивает действительную скорость движения и профиль толщины, т. е.

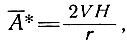
(7)

а для случая нулевой дивергенции

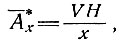
(7б)

а именно, половина величины аккумуляции при тех же скорости и профиле толщины, которые требуются для идеально круглого куполового ледника.

Аналогично этому можно воспользоваться формулой (16) и получить для накопления равновесия

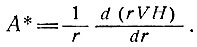
(8)