8. Резюме

Хотя общие уравнения движения массы ледника с плотностью ρ при σ_ij (напряжениях в точках х_i) и Х_i (внешних силах)

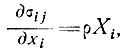
(1)

с трудом поддаются решению для движущихся масс ледников, в некоторых случаях можно получить их решения относительно скорости движения и градиента скорости благодаря особым типам симметрии, встречающимся в движущемся леднике. Для этого нужно рассмотреть градиенты напряжения и градиенты скорости: 1) по ширине поперек линии движения ледника, 2) вертикально от поверхности до ложа, 3) соосно с линией движения.

Причина этого в том, что соответствующие градиенты скорости имеют наибольшие величины в различных частях движущегося ледника, т. е. поперечные градиенты скорости (по вертикали и горизонтали) имеют около границы максимальные значения, а на поверхности и в центре ледника - минимальные, в то время как для продольных градиентов скорости справедливо обратное утверждение. Непосредственное взаимодействие градиентов скорости происходит лишь в некоторых случаях, которые здесь не рассматриваются.

При заранее заданном законе течения льда, т. е. если нам известна связь между девиатором напряжения и скоростью деформации льда, например, вида

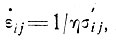
(2)

где η - функция температуры и инвариантов напряжения, уравнения движения могут быть записаны в величинах скоростей деформации, решены численно и в конечном итоге определены скорости по всей массе льда с учетом граничных условий, т. е. как функции формы и размера массы ледника и скорости движения и деформации в некотором положении.