
6.2. Глетчеры
6.2.1. Общие уравнения движения. Исследуем сначала продольную скорость вдоль глетчера с параллельными сторонами, у которого на расстоянии х вдоль центральной линии площадь поперечного сечения А, средняя толщина Z, наклон основания β, а средний коэффициент трения на границе 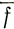 . Рассмотрим уравнения (12) и (13) подраздела 5.2, пренебрегая при этом конечным членом правой части уравнения (12), в соответствии с данными подраздела 5.1:
. Рассмотрим уравнения (12) и (13) подраздела 5.2, пренебрегая при этом конечным членом правой части уравнения (12), в соответствии с данными подраздела 5.1:
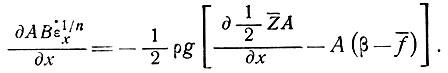
(20)
На практике у большинства глетчеров форма поперечного сечения медленно изменяется с изменением параметра х. Тогда главным фактором, влияющим на скорость по мере изменения площади поперечного сечения, будет средняя толщина 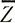 . Таким образом, если мы запишем
. Таким образом, если мы запишем
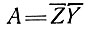
(21)
и если средняя ширина 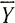 медленно изменяется с изменением параметра х, можем принять более простое уравнение (17) подраздела 5.2, аналогичное двухмерному уравнению
медленно изменяется с изменением параметра х, можем принять более простое уравнение (17) подраздела 5.2, аналогичное двухмерному уравнению
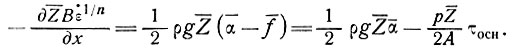
(22)
Величины с чертой являются средними значениями по поперечному сечению, значение τосн определяется уравнением (5) подраздела 5.2 и
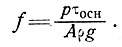
(23)
Разность скоростей Vп - Vосн вдоль центральной линии между поверхностью и основанием можно выразить в величинах τосн, пользуясь равенством τxz = s2ρgαz и законом течения, и интегрируя от 0 до Z - толщины в центре:
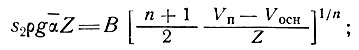
(24)
здесь s2 - коэффициент формы конкретного поперечного сечения, который можно оценить эмпирически по расчетам Ная, как это изложено в разделе 2.
Введем другой коэффициент формы, определяемый выражением
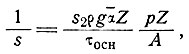
так что, согласно уравнению (22), окончательное уравнение приобретает вид
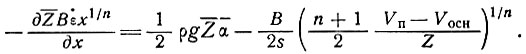
(25)
Скорость движения базисного слоя - параметр, который трудно вычислить. Хотя относительно скольжения глетчеров выдвинуто несколько теорий, например Вертман [139, 140, 145, 147], Либутри [62, 65, 67], однако их соответствие эксперименту не совсем удовлетворительное (см. [73]). Проведенные до сих пор эмпирические измерения скольжения глетчеров также неадекватны. Измерения горизонтальной скорости по вертикальным скважинам до настоящего времени ограничивались глубинами, на которых термобур не может работать. Это приводит к тому, что остается неисследованной очень интересная зона перехода у основания глетчера, которая может представлять собой резкий переход на поверхности раздела лед - скальное ложе или включать песок, морену или смесь льда и скальной породы. В общем, трудно будет провести различие между чистым скольжением, большим сдвигом во льду у основания или комбинацией большого сдвига и скольжения в базисном слое, состоящем из смеси лед - скала. В данной работе предлагается сначала рассчитать влияние раздельного движения. Это позволит проанализировать движение скольжения на основании сопоставления с теориями скольжения по дну.
Если не имеется скольжения у основания, то уравнение (25) (отбрасывая черту, обозначающую осреднение) примет вид
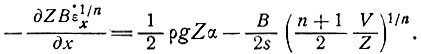
(26)
Это и есть основополагающее уравнение продольной скорости движения льда вдоль центральной линии ледника и градиента его скорости как функции толщины льда, наклона поверхности, формы поперечного сечения и параметров закона течения льда. Если глетчер расширяется или сужается, так что поперечное растяжение или сжатие существенны, то вместо 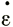 х берем (см. подраздел 5.3)
х берем (см. подраздел 5.3)
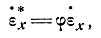
(27)
где
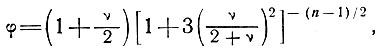
а ν - отношение скорости боковой деформации к продольной.
![Рис. 6.1. Продольный профиль глетчера Атабаска [99], сглаженные средние на протяжении 1200 м. 1 - поверхность ледника, 2 - ложе, 3 - сглаженные средние](pic/000654.jpg)
Рис. 6.1. Продольный профиль глетчера Атабаска [99], сглаженные средние на протяжении 1200 м. 1 - поверхность ледника, 2 - ложе, 3 - сглаженные средние
Заметим, что величины n и В в левой и правой частях уравнения (26) вообще будут различны из-за неодинаковых диапазонов напряжений для каждого случая. Поскольку сдвиг у основания может быть примерно равен 1 бару, то, чтобы величины n и В имели разумные значения, скорость продольной деформации должна была бы быть 1/10 лет-1. Поскольку в типичных глетчерах с небольшим наклоном средние скорости продольной деформации более 1/30 лет-1 необычны в ненарушенных областях, то для левой части уравнения можно ожидать меньшие значения параметра n.
Уравнение (26) можно использовать для определения: 1) распределения скорости массы ледника при данных размерах ледника и параметрах закона течения льда и 2) соответствующих параметров закона течения при данных размерах массы ледника и распределения скорости в нем. Поскольку параметры закона течения для естественно деформирующегося льда до сих пор недостаточно известны, рассмотрим п. 6.2.2.
6.2.2. Наблюдаемое соотношение зависимостей между скоростью движения ледника и наклоном его поверхности (сглаженным). Возьмем типичный глетчер (глетчер Атабаска в провинции Альберта, Канада), который был детально измерен по толщине, наклону поверхности, форме поперечного сечения и скорости вдоль центральной линии [51, 100 - 03]. Величины некоторых параметров, полученных для этого глетчера, представлены на рис. 6.1, в табл. 6.1, и на рис. 3.5 - для профилей поперечного сечения.
Таблица 6.1
Физические параметры глетчера Атабаска
| № участка | х, м | h, м | α° | -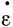 10-3 год-1 10-3 год-1 |
Z, м | Z11, м | α°10·102 |
| 10 | 0 | 458 | 4,5 | 103 | 310 | - | 450 |
| 11 | 82 | 452 | 4,0 | 74 | 318 | - | 376 |
| 12 | 180 | 447 | 2,8 | 42 | 323 | - | 344 |
| 13 | 279 | 442 | 2,8 | 34 | 320 | - | 356 |
| 14 | 380 | 437 | 3,1 | 23 | 317 | 317 | 371 |
| 15 | 477 | 431 | 3,6 | 22 | 320 | 316 | 350 |
| 16 | 618 | 422 | 4,1 | 21 | 322 | 316 | 325 |
| 17 | 761 | 412 | 4,3 | 19 | 314 | 313 | 308 |
| 18 | 910 | 401 | 4,2 | 22 | 312 | 309 | 308 |
| 19 | 1046 | 392 | 3,2 | 18 | 310 | 303 | 312 |
| 20 | 1199 | 386 | 1,9 | 7 | 318 | 397 | 318 |
| 21 | 1362 | 381 | 1,7 | 1 | 310 | 290 | 324 |
| 22 | 1517 | 376 | 2,2 | 4 | 290 | 284 | 334 |
| 23 | 1669 | 369 | 2,8 | 3 | 273 | 276 | 351 |
| 24 | 1811 | 362 | 3,2 | 1 | 260 | 264 | 371 |
| 25 | 1951 | 353 | 3,8 | -1 | 248 | 251 | 395 |
| 26 | 2042 | 348 | 4,2 | 2 | 248 | 237 | 418 |
| 27 | 2115 | 342 | 5,2 | -3 | 248 | 242 | 448 |
| 28 | 2211 | 331 | 6,2 | 7 | 225 | 221 | 490 |
| 29 | 2354 | 315 | 6,4 | 18 | 186 | 207 | 543 |
| 30 | 2431 | 296 | 5,9 | 9 | 170 | 293 | 603 |
| 31 | 2711 | 281 | 4,4 | 4 | 155 | 178 | 657 |
| 32 | 2859 | 270 | 5,0 | 2 | 118 | 162 | 752 |
| 33 | 2954 | 262 | 6,8 | 6 | 115 | 145 | 897 |
| 34 | 3049 | 250 | 8,6 | 14 | 113 | 129 | 1132 |
| 35 | 3130 | 237 | 9,8 | 17 | 100 | 97 | 1246 |
| 36 | 3321 | 206 | 9,8 | 16 | 90 | 85 | 1466 |
| 37 | 3450 | 180 | 14,6 | 31 | 73 | - | 1745 |
| 38 | 2560 | 144 | 21,2 | -10 | 56 | - | 2260 |
| 39 | 3603 | 131 | 23,0 | - | 43 | - | 3200 |
Отмечаются флуктуации наклона поверхности и скорости деформации на сравнительно небольшом расстоянии (0,5 - 1,2 км), которые позволяют предполагать, что трение в базисном слое 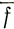 следует сглаженному наклону поверхности (на 1200 м). Отсюда сначала исследуем связь для сглаженного наклона скорости V, толщины Z и наклона α в отсутствии скольжения по дну, т. е. уравнение (26) с нулевым градиентом скорости деформации:
следует сглаженному наклону поверхности (на 1200 м). Отсюда сначала исследуем связь для сглаженного наклона скорости V, толщины Z и наклона α в отсутствии скольжения по дну, т. е. уравнение (26) с нулевым градиентом скорости деформации:
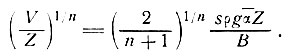
(29)
Величины параметров для этого уравнения, полученные на глетчере Атабаска, показаны на двойной логарифмической шкале (рис. 6.2). Сглаживание было проведено на расстоянии 1100 м. Величина коэффициента формы была оценена по результатам расчетов профилей скорости Наем [92, 93] для различных форм поперечного сечения и измеренных поперечных сечений глетчера по Патерсону (см. рис. 3.7).
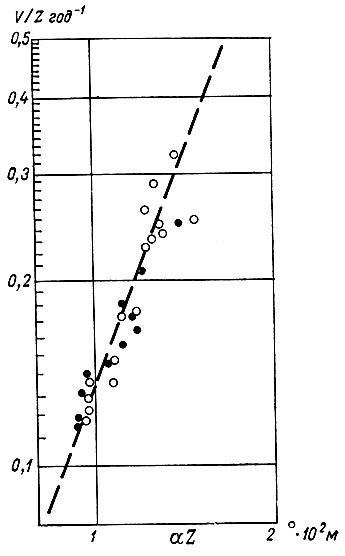
Рис. 6.2. Зависимость V/Z от αZ в прямоугольных координатах в логарифмическом масштабе, рассчитанная по рис. 6.1, для глетчера Атабаска. Наклон пунктирной линии предполагает величину показателя степенного закона n ≈2,6
Отсюда n = 2,6, а B = 0,63×109 дин/ (см2 · с1/3). Эти величины удовлетворительно согласуются с другими результатами измерений параметров течения в лабораторных и полевых условиях при температуре, близкой к точке таяния.
Разброс точек на рис. 6.2 можно объяснить влиянием ряда факторов: флуктуаций на более коротких расстояниях, погрешностей измерения и других параметров, не рассматриваемых здесь, скольжения по дну и изменения коэффициента формы вдоль глетчера. Несмотря на эти отклонения, полученные результаты позволяют считать, что уравнение (29) дает хорошее приближение для значений сглаженной скорости, выраженной через другие параметры. Однако для несглаженных значений это отношение полностью заменяется еще более мелкомасштабными флуктуациями наклона, показанными на рис. 6.1, которые будут подробно исследованы ниже.
6.2.3. Скорость деформации и флуктуации наклона. Рассмотрим мелкомасштабные флуктуации скорости деформации и наклона. Имеется уравнение
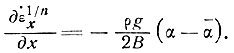
(30)
Допустим, что для глетчера умеренного пояса параметр В постоянен вдоль языка, и отсюда, интегрируя выражение (30) в пределах 1/2 длины волны, получим величины отклонений скорости деформации Δ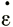 х и напряжения ρgΔα для каждой из 1/2 длины волны. Диапазон величин здесь недостаточен, чтобы точно определить показатель степенного закона n, но этот диапазон соответствует низкому значению n. Отсюда мы определяем величину В, осредняя результаты по длине глетчера и принимая n = 1, чтобы получить В = 0,70 · 109 дин (см2 · с1/3).
х и напряжения ρgΔα для каждой из 1/2 длины волны. Диапазон величин здесь недостаточен, чтобы точно определить показатель степенного закона n, но этот диапазон соответствует низкому значению n. Отсюда мы определяем величину В, осредняя результаты по длине глетчера и принимая n = 1, чтобы получить В = 0,70 · 109 дин (см2 · с1/3).
Эти параметры справедливы для всей толщины льда, в то время как другие (см. п. 6.2.2) связаны с областью высокого сдвига у основания.
Для большинства глетчеров умеренных поясов изменение их температуры не очень велико, так что нет оснований ожидать, что значения В будут значительно меняться по глетчеру. Однако на основании исследования кривизны закона течения, представленного в двойных логарифмических шкалах, вблизи В = 1 бару можно ожидать, что значения В, полученные для различных диапазонов напряжения, будут несколько изменяться в зависимости от того, насколько эти диапазоны напряжения отличаются от приведенного значения В.
Пункты 6.2.2 и 6.2.3 предназначены служить не более чем руководством к применению общих результатов теории скоростей продольной деформации, разработанной для ледниковых масс, к глетчерам умеренных поясов.
Метод определения величин параметров течения по профилю продольной скорости служит дополнением к методам, использованным Патерсоном и Саважем [100 - 102] и др., анализировавшими при изучении закона течения льда только поперечные и вертикальные профили скорости.
6.2.4. Сжатие и растяжение. Из уравнений, выведенных для продольной скорости и скорости деформации, можно составить некоторые общие представления относительно форм ледниковых масс, подвергающихся сжатию или растяжению. Нами в общих чертах анализируется лишь один простой случай. Результаты этого анализа без больших затруднений можно распространить на исследование влияния изменений высоты ложа, коэффициента формы и т. п., используя численные методы.
Для глетчера на плоском ложе продольный градиент толщины равен наклону поверхности, т. е.
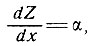
(31)
где ось х имеет направление, противоположное направлению движения. Заметим, что скорость движения поверхности V в отсутствие скольжения определяется уравнением (29) для сглаженных наклона и толщины:
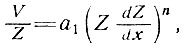
(32)
где α1 = const. Тогда уравнение (31) запишем как
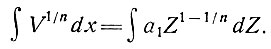
Из этого уравнения можно найти формы профиля толщины льда, которые вызывают увеличение или уменьшение скорости вдоль линии тока. Типичный профиль глетчера Z(x) можно аппроксимировать уравнением вида
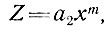
(33)
где х - расстояние от фронта ледника против направления движения, а а2 и m - константы (m = 2, 1, 1/2, 1/3, 1/4Ο, ...)o Тогда
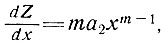
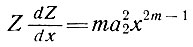
и
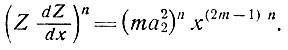
Отсюда и из уравнения (32) находим для скорости
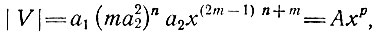
(34)
где, скажем,
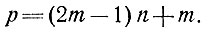
Далее, скорость постоянна, когда р равно нулю, а именно, когда (2m+1) n + m = 0, т. е.
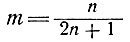
(35)
и при n = 1, 2, 3, 4, ... ∞, m = 1/3, 2/5, 3/7, 4/9, .. , 1/2.
Таким образом, для массы ледника с плоским основанием и поверхностью вида Н = ахm скорость убывает при движении в глубь материка (растяжение) при m < 3/7 и n = 3, или при m < 4/9 и n = 4. При m > 3/7 (n = 3) скорость движения ледника возрастает в глубь континента и имеет место сжатие.
Отметим, что при идеально пластичной среде (n = ∞) для нулевой скорости продольной деформации необходим параболический профиль m = 1/2. При меньших величинах n для постоянной скорости требуются несколько более изогнутые профили (m > 1/2).
Кроме того, для дивергентного течения при любом n требуется несколько более изогнутый профиль (m < 1/2), чем профиль, соответствующий случаю нулевой деформации. В разделе 7 формы профилей высоты ледниковых масс будут рассмотрены более подробно.
6.2.5. Волны на поверхности глетчера (постоянная толщина льда). В качестве дополнения к подразделу 5.4 рассмотрим изменение скорости деформации для идеальных поверхностных волн, скажем, типичных для волн, наблюдающихся на глетчере Атабаска. Предположим, что мы имеем глетчер с волнообразной поверхностью, наклон которой может быть представлен уравнением
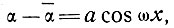
где λ = 2π/ω - длина волны колебаний.
Уравнение (30) теперь принимает вид
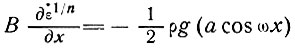
(36)
или
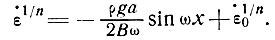
(37)
Результаты исследования течения, изложенные в разделе 2, предполагают, что, если скорости деформации малы, можно принять n ≈ 1, тогда
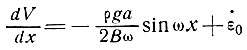
(38)
и
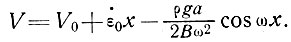
(39)
Следовательно, максимумы скорости имеют место в положениях максимумов наклонов поверхности ледника. Максимальное растяжение реализуется на гребнях относительных возвышений (холмов), а относительное сжатие проявляется в виде максимумов во впадинах. Что это именно так, можно видеть на рис. 6.1, где представлены градиенты скорости деформации и наклоны поверхности ледника, примерно совпадающие по фазе. Можно ожидать, что это отношение нарушится около фронта глетчера, где градиентом толщины льда нельзя пренебречь.
Аналогичные свойства скорости деформации и флуктуаций наклона наблюдались на поверхности куполовых ледников, которые будут рассмотрены в следующем подразделе.
|
ПОИСК:
|
© GEOMAN.RU, 2001-2021
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'