
6.3. Куполовые ледники
У куполовых ледников, если в основной массе ледника нет "потока" с большей скоростью течения, единственной границей, сдерживающей лед, является их ложе. Осложнения, вызываемые "потоками", пока не будут рассматриваться. В куполовом леднике, таким образом, нет горизонтального поперечного сдвига и проблема динамики такого ледника в данном случае становится аналогичной проблеме динамики шельфового ледника, за исключением того, что в куполовом леднике скорость изменяется по вертикали, в то время как у шельфового ледника - по двум координатам (х и у). В обоих случаях поперечные сечения к линии течения соответствуют бесконечным плитам с коэффициентом формы, равным 1.
6.3.1. Скорость и сглаженный наклон. Пренебрегая в данный момент влиянием продольных деформаций и поперечных сжатий или растяжений, т. е. при условии, что в уравнении (29) подраздела 5.3
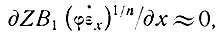
можно ожидать, что зависимость между сглаженной скоростью V, толщиной Z и углом наклона 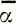 в общем справедлива:
в общем справедлива:
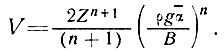
(40)
Это соответствует уравнению (3) для куполовых ледников в случае замены обозначения половины ширины а толщиной Z и уравнению (29) для глетчеров (при коэффициенте формы, равном единице).
В качестве примера, насколько полно эти представления отражают действительную картину в куполовом леднике вдоль линии его тока, рассмотрим локальный куполовый ледник, имеющий 200 км в диаметре, поблизости от ст. Уилкс (рис. 6.3 и 6.4) и исследует его профили от купола до мысов Пойнсетт и Фольгер (см. Макларен [71] и Пфитцнер [103]). На рис. 6.5 для эти двух профилей показаны графики 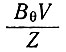 в функции от αZ. Из этих графиков видно, что линейное отношение в логарифмических координатах, видимо, остается достаточно правильным и что n = 3,4, В = 0,85 · 109 дин/Дсм2 · с1/3).
в функции от αZ. Из этих графиков видно, что линейное отношение в логарифмических координатах, видимо, остается достаточно правильным и что n = 3,4, В = 0,85 · 109 дин/Дсм2 · с1/3).
Величина В зависит от температуры. Поэтому здесь принято, что она изменяется с температурой θ в соответствии с уравнением
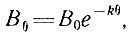
где k≈10-1 °С-1. Отсюда величина В была выведена для различных значений температуры θ в базисном слое, которая была рассчитана в разделе 4 вдоль профиля от купола до мыса Пойнсетт.
Результаты расчетов температуры (см. рис. 4.15) предполагают, что температуры в базисном слое изменяются с температурой поверхности, но они несколько выше, причем средняя их величина вдоль линии тока масс льда составляет примерно -10° С.
![Рис. 6.3. Профили куполового ледника Уилкса по линии купол - мыс Фольгер [71]. а - поверхность; б - средняя толщина льда; в - ложе. Сетки деформации: I - DA, II - В, III - С, IV - D; г - относительная высота поверхности, м; д - наклон поверхности; е - аккумуляция; ж - скорость продольной деформации на поверхности, 1 - сглаженные величины, 2 - частные величины](pic/000682.jpg)
Рис. 6.3. Профили куполового ледника Уилкса по линии купол - мыс Фольгер [71]. а - поверхность; б - средняя толщина льда; в - ложе. Сетки деформации: I - DA, II - В, III - С, IV - D; г - относительная высота поверхности, м; д - наклон поверхности; е - аккумуляция; ж - скорость продольной деформации на поверхности, 1 - сглаженные величины, 2 - частные величины
Наконец, после того как построен график для скорости деформации 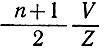 в функции от напряжения ρgZαеk, приведенного к постоянной температуре (см. рис. 2.2), становится очевидным, что эти значения скорости напряжения и деформации соответствуют значениям скорости напряжения и деформации в том диапазоне, который рассчитан для температур в базисном слое вдоль рассматриваемого профиля (см. рис. 4.16). Однако для полного подтверждения значений упомянутых температур придется подождать завершения программы бурения и температурных измерений в рассматриваемом районе.
в функции от напряжения ρgZαеk, приведенного к постоянной температуре (см. рис. 2.2), становится очевидным, что эти значения скорости напряжения и деформации соответствуют значениям скорости напряжения и деформации в том диапазоне, который рассчитан для температур в базисном слое вдоль рассматриваемого профиля (см. рис. 4.16). Однако для полного подтверждения значений упомянутых температур придется подождать завершения программы бурения и температурных измерений в рассматриваемом районе.
![Рис. 6.4. Профили куполового ледника Уилкса по линии купол - мыс Пойнсетт [71, 103]. а - поверхность; б - средняя толщина льда. Сетки деформации: I - D, II - G, III - Н, IV - I; в - ложе, г - относительная высота поверхности, д - наклон поверхности, е - аккумуляция, ж - скорость продольной деформации, з - скорость продольного движения. 1 - средние значения на расстоянии 3,5 км, 2 - локальные величины](pic/000683.jpg)
Рис. 6.4. Профили куполового ледника Уилкса по линии купол - мыс Пойнсетт [71, 103]. а - поверхность; б - средняя толщина льда. Сетки деформации: I - D, II - G, III - Н, IV - I; в - ложе, г - относительная высота поверхности, д - наклон поверхности, е - аккумуляция, ж - скорость продольной деформации, з - скорость продольного движения. 1 - средние значения на расстоянии 3,5 км, 2 - локальные величины
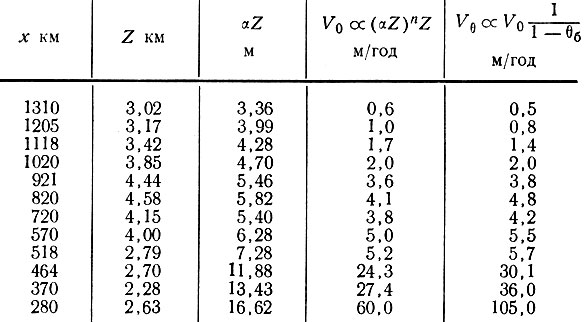
Формулу (40) для сглаженной скорости можно также использовать для оценки скорости движения большого куполового ледника в направлении в глубь континента, если известны его толщина и наклон, а также скорость у края. В качестве примера такого использования этой формулы рассчитаем функцию (αZ)nZ для профиля от ледника Уилкса в глубь континента. Это позволит определить величину V0 вдоль этой линии при условии, если бы температуры в базисном слое были постоянными, т. е. принимая значение B0 постоянным и равным, скажем, 109 дин/(см2 · с1/3). Согласно разделу 4, получаем оценку температур в базисном слое вдоль профиля, рассчитанных по этим скоростям. Наконец, используя полученные величины температур в базисном слое, можно рассчитать новые значения скорости Vθ, которые учитывают изменение температуры вдоль профиля (табл. 6.2). Эту процедуру можно повторить, чтобы получить новые величины температур и скорости, до тех пор пока не будет достигнута сходимость результатов. Поскольку, однако, другие параметры в этой области Антарктиды, такие, как поперечная деформация и кривизна линий тока, до сих пор остаются неизвестными, более совершенный двухмерный анализ на данном этапе исследований не будет предпринят.
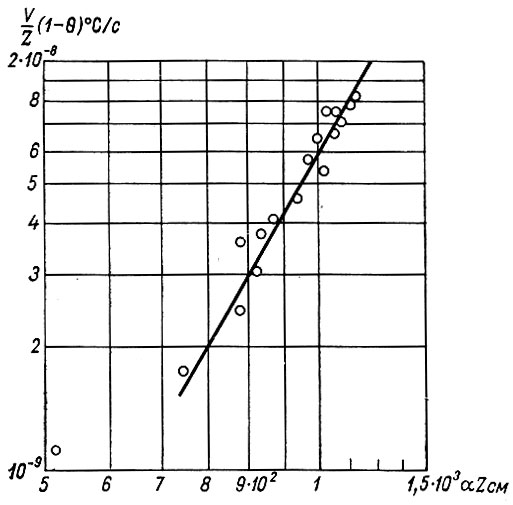
Рис. 6.5. Зависимость величины отношения V/Z от осредненной величины αZ с поправками на расчетные температуры θ вдоль линии купол ледника Уилкса - мыс Пойнсетт
Таблица 6.2
Расчетные скорости на линии ст. Уилкс - ст. Восток
6.3.2. Скорость деформации и флуктуации наклона. Рассмотрим небольшие изменения наклона поверхности ледника, вызывающие аналогичные изменения в скорости деформации, наложенные на сглаженную скорость, общий наклон и толщину льда.
Такие коротковолновые флуктуации подчиняются уравнению
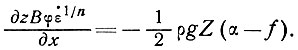
(41)
Это уравнение можно также проверить по данным для куполового ледника Уилкса.
Прежде всего заметим, что вдоль участка этого ледника купол - мыс Пойнсетт вне пределов сетки деформации G боковые деформации были меньше продольных и, таким образом, в соответствии с уравнениями (27) и (28) подраздела (5.3) они не оказывают существенного влияния. На рис. 6.6. показано хорошее соответствие между градиентом скорости деформации и наклоном поверхности. Исследовав величину соответственных изменений, можно получить значения n и В из выражения
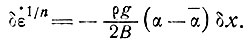
(42)
Эти результаты иллюстрируются данными рис. 6.7, где показано, что октаэдрическое сдвиговое напряжение, определяемое правой стороной уравнения, изменяется от 0,6 до 0,25 бара.
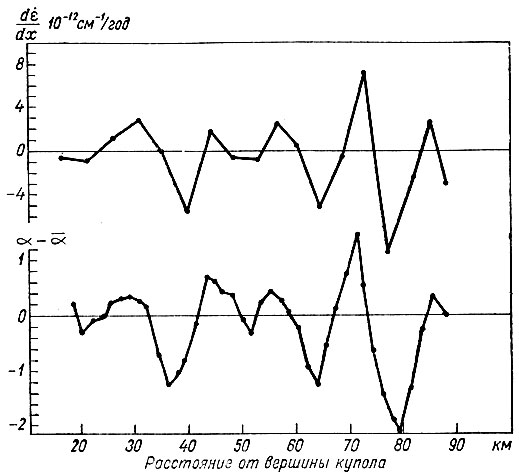
Рис. 6.6. Градиент скорости деформации и флуктуации наклона поверхности куполового ледника Уилкса
![Рис. 6.7. График зависимости скорости деформации сдвига от напряжения сдвига после интегрирования по 1/2 длины волны [73]](pic/001000.jpg)
Рис. 6.7. График зависимости скорости деформации сдвига от напряжения сдвига после интегрирования по 1/2 длины волны [73]
Величины параметров n и В следующие: n= 1,2, 5 = 1,5 × 109 дин/(см2 · с1/3), или 3,4 · 1015 дин/(см2 · с). Низкое значение n отражает почти ньютоновскую вязкость при низких напряжениях, как сообщали другие авторы (например, Буткович и Ландауэр [21], Меллор и Смит [80]).
Величина параметра В имеет здесь среднее значение, характерное для всей колонки массы ледника (см. рисунок), т. е. около основания преобладает простой сдвиг. Но для большей части колонки деформация представляет собой продольное растяжение или сжатие в горизонтальной и вертикальной плоскостях, причем направление максимального сдвига находится под углом 45° к направлению растяжения и сжатия.
Масса ледника
Чтобы сравнить величину параметра В здесь с величиной параметра В других измерений, необходимо преобразовать значения продольных напряжений σх и деформаций 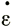 х уравнения (42) в соответствующие величины октаэдрического напряжения τ0 и деформации γ0 по Наю [83] для двух измерений (см. подраздел 2.1):
х уравнения (42) в соответствующие величины октаэдрического напряжения τ0 и деформации γ0 по Наю [83] для двух измерений (см. подраздел 2.1):
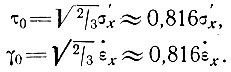
Величины δх в уравнении (42) пока еще не определены, но, чтобы получить максимальное изменение напряжения, нам нужно проинтегрировать по 1/2 длины волны, т. е.
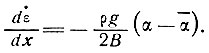
Если мы имеем регулярные колебания с длиной волны λ на поверхности, определяемые выражением
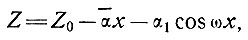
где
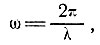
т. е.
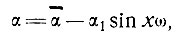
тогда
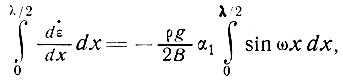
откуда

или
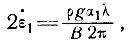
где 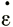 1 - амплитуда изменений скорости деформации.
1 - амплитуда изменений скорости деформации.
В значениях октаэдрического сдвига
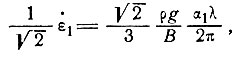
или
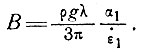
Интересно также отметить, что максимальное изменение октаэдрического сдвигового напряжения у основания равно
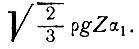
Отсюда длина волны, при которой напряжение сдвига, производимое продольным напряжением, равно увеличению напряжения сдвига в базисном слое, выражается как
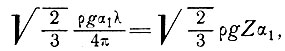
т. е.
λ = 4πZ
Этот результат предполагает, что волны большей длины могли бы учитываться формулой для сглаженной скорости (уравнение 40).
По рис. 6.7 (для октаэдрического сдвигового напряжения в функции от скорости деформации) и рис. 2.2 (для закона течения льда) можно видеть, что величина параметра В, определенная выше, вероятно, могла бы соответствовать средней температуре колонки -15°С с отклонениями от этой величины вдоль линии тока согласно с изменением средней температуры. Эта температура кажется соизмеримой со средней температурой в массе ледника в том виде, в котором ее можно оценить по расчетам раздела 4 (см. рис. 4.16). Здесь опять для более точного анализа придется подождать результатов измерений по всему куполовому леднику. При больших скоростях деформации величина параметра n может быть значительное больше единицы. В этом случае необходимо осуществлять анализ более общего характера (приложение II), в котором для нелинейного закона течения должно учитываться влияние горизонтального сдвига.
6.3.3. Влияние поперечной деформации на профиль продольной скорости в куполовых ледниках. По результатам анализа уравнений (27) и (28) подраздела 5.3 можно видеть, как наличие поперечной деформации влияет на зависимость продольной деформации от напряжения. Заметим, что небольшая поперечная деформация оказывает незначительное влияние на продольную деформацию такого же знака в уравнении (41). Большая поперечная деформация, особенно при противоположных знаках, сильно влияет на зависимость продольной деформации от напряжения.
В качестве первого примера влияния поперечной деформации рассмотрим результаты измерений сетки деформации в области купола куполового ледника Уилкса в том виде, в каком они представлены в табл. 6.3.
Таблица 6.3
Сетки деформации куполового ледника Уилкса
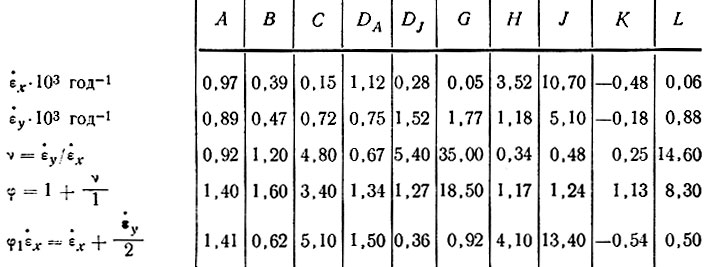
Отметим здесь, что, согласно Макларену [71], эти сетки деформации представляли собой маленькие розетки с тремя сторонами длиной 100 м.
Уравнение (29) подраздела 5.1 показывает, что изменения скорости деформации на небольших расстояниях (длины волн 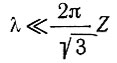 ) могут быть очень большими. Сравнение величин деформационной сетки с теллурометрическими измерениями на больших расстояниях (см. рис. 6.3, 6.4, 6.8) показывает, что в данном регионе это явление действительно имеет место.
) могут быть очень большими. Сравнение величин деформационной сетки с теллурометрическими измерениями на больших расстояниях (см. рис. 6.3, 6.4, 6.8) показывает, что в данном регионе это явление действительно имеет место.
![Рис. 6.8. Поперечный профиль куполового ледника Уилкса по линии мыс Пойнсетт - мыс Фольгер [73]. а - средняя толщина льда; б - поверхность ледника. Сетка деформации: I - A, II - L, III - K, IV - J; в - ложе, г - относительная высота поверхности, д - наклон поверхности, е - аккумуляция, ж - скорость продольной девормации на поверхности. 1 - сглаженные величины, 2 - частные величины](pic/000707.jpg)
Рис. 6.8. Поперечный профиль куполового ледника Уилкса по линии мыс Пойнсетт - мыс Фольгер [73]. а - средняя толщина льда; б - поверхность ледника. Сетка деформации: I - A, II - L, III - K, IV - J; в - ложе, г - относительная высота поверхности, д - наклон поверхности, е - аккумуляция, ж - скорость продольной девормации на поверхности. 1 - сглаженные величины, 2 - частные величины
Для тех деформационных сеток, в которых преобладает поперечная деформация, непосредственная связь между продольными наклоном и скоростью деформации незначительна, если не принимать во внимание коэффициент деформации φ. Это свидетельствует о большой роли скорости поперечной деформации в динамике куполовых ледников. Поскольку единственными скоростями деформации, которыми мы в настоящее время располагаем для профилей линии тока DJ и DA ледника Уилкса, являются локальные величины в узлах сетки деформации, нельзя должным образом на данном этапе исследований проверить влияние поперечной деформации и корректность уравнений, выведенных в подразделе 5.3. Однако согласно данным табл. 6.3, оказывается, что величина параметра вязкости В, рассчитанная по уравнению (42) для этой линии, могла бы иметь погрешность, в два раза большую, если бы поперечная деформация не была учтена. Линия побережья JA (рис. 6.9) большей частью расположена поперек линии тока масс льда, и высокая корреляция между относительными высотами и скоростями деформации (см. рис. 6.8) указывает на то, что уравнение (42) действует поперек линии тока, так же как и вдоль нее, что оправдывает учет коэффициента поперечной деформации. Чтобы преодолеть трудность учета поперечной деформации, дополнительный ряд больших сеток деформации был установлен Д. Картером в 1967 г. в промежуточных положениях между сторонами треугольника. Отсюда приходим к выводу, что трехсторонний траверс, который дает возможность получать непрерывные данные о деформации вдоль всего маршрута, более ценен, чем линейный переход, в котором измеряются только расстояния и углы.
![Рис. 6.9. Измеренные скорости, горизонтали поверхности и линии тока ледника Уилкса, изображенные в виде ортогоналей к горизонталям [103]. Буквы - сетки деформации. Высоты в метрах](pic/000708.jpg)
Рис. 6.9. Измеренные скорости, горизонтали поверхности и линии тока ледника Уилкса, изображенные в виде ортогоналей к горизонталям [103]. Буквы - сетки деформации. Высоты в метрах
Далее, скорость поперечной деформации также влияет на сглаженный профиль продольной скорости. Однако это влияние обычно невелико и вообще может рассматриваться вместе с влиянием скорости продольной деформации. Тогда из общего уравнения (39) подраздела 5.1, пренебрегая последним членом его правой части и включив коэффициент φ, получим
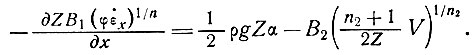
(43)
Приняв сглаженные величины скорости на расстояниях х ≈ 15Z, устанавливаем, что член в левой части уравнения (43) мал. Откуда для сглаженной скорости получим
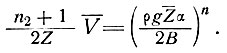
(44)
Однако, когда первым членом, который мы можем записать, например, как
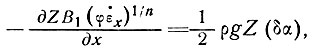
(75)
нельзя пренебречь, выражение для сглаженной скорости имеет вид
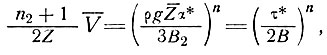
(46)
где
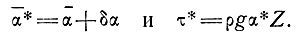
Это позволяет ввести поправки в профили сглаженной скорости, учитывающие высокие скорости продольной и поперечной деформации. В табл. 6.4. приведены величины поправок, рассчитанные по значениям поперечных деформаций вследствие дивергенции линий тока льда, которые имеют место для куполового ледника Уилкса на линиях купол - мыс Пойнсетт и купол - мыс Фольгер. Использованная при этом величина В1 была определена для случая изменений скорости деформации на волнообразных колебаниях ложа. Эти поправки введены в расчеты параметров течения, которые были рассмотрены в этом разделе. Наибольшая поправка менее 10%, но она все же существенна при определении величины параметра n2 закона течения льда.
6.3.4. Скорость деформации и линии тока. В идеально круглом куполовом леднике, текущем по прямым линиям от центра, скорость поперечной деформации 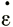 θ определяется скоростью V и углом дивергенции θ, зависящим от расстояния r от центра. Если у = rθ, то скорость поперечной деформации находится как
θ определяется скоростью V и углом дивергенции θ, зависящим от расстояния r от центра. Если у = rθ, то скорость поперечной деформации находится как
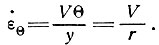
(78)
или
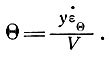
Таблица 6.4
Поправки к сдвиговому напряжению с учетом скорости деформации
| Профиль D → А (рис. 6.9) | Расстояние от точки D, км | τ | Сдвиговое напряжение δτ, бары | τ* | Профиль D → J (рис. 6.9) | Расстояние от точки D, км | τ | Сдвиговое напряжение δτ, бары | |
| D | 0-23 | 0,52 | -0,05 | 0,47 | D | 0-18 | 0,28 | 0 | 0,28 |
| С | 23-63 | 0,68 | 0 | 0,68 | G | 18-50 | 0,70 | -0,01 | 0,69 |
| В | 63-92 | 0,77 | 0,01 | 0,78 | Н | 50-75 | 0,85 | 0,02 | 0,87 |
| А | 92-110 | 0,92 | 0,02 | 0,93 | J | 75-101 | 1,20 | 0,60 | 1,26 |
Такой идеальный куполовый ледник характеризуется круговой симметрией относительно центра, он хорошо аппроксимируется куполовым ледником с гладким плоским основанием и концентрическими круговыми контурами. В реально существующих куполовых ледниках нерегулярные контуры поверхности и изменяющиеся профили ложа вызывают дивергенцию и конвергенцию линий тока масс льда (см. рис. 6.9).

а - идеальный куполовый ледник (круговые контуры, простое радиальное течение), б - нерегулярный куполовый ледник. 1 - конвергенция, 2 - дивергенция
Если скорости деформации и движения известны, то угол дивергенции θ между двумя линиями тока масс льда на расстоянии у друг от друга можно рассчитать по выражению
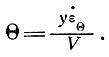
Влияние кривизны линий тока на распределение продольной скорости (и результирующую поперечную деформацию) тогда можно вычислить с помощью уравнений (45) и (46).
На рис. 6.9 представлены линии тока для локального куполового ледника Уилкса, полученные в виде нормалей к контурам ледников. Показано, что фактические направления измеренной скорости хорошо согласуются с ними. В табл. 6.5 приведены величины скорости поперечной деформации, рассчитанные по дивергенциям линий тока, и фактические величины, измеренные в узлах сеток деформации. Между ними существует общее соответствие, но измеренные скорости деформации гораздо меньше по масштабу и обнаруживают значительно большие флуктуации. Это означает, что для получения подробного представления о дивергенции линий тока требуются сетки деформаций очень крупного масштаба (около 15 км).
Таблица 6.5
Скорость поперечной деформации в куполовом леднике Уилкса (рис. 6.9)
| Сетка деформации | Скорость деформации | Дивергенция течения | Угол к линии тока массы льда, град. |
| А | 5,0 · 10-4/год | 2,8 | 21 |
| В | 4,5 | 2,0 | 8 |
| С | 8,0 | 2,2 | 34 |
| DJ | 7,5 | 3,5 | - |
| М | 10,0 | 3,7 | 5 |
| N | 5,7 | 2,3 | 13 |
| DJ | 15,2 | 3,6 | - |
| G | 7,5 | 2,1 | 41 |
| Н | 12,0 | 6,9 | 16 |
| J | 44,0 | 14,7 | 13 |
| К | -0,2 | -3,0 | 0 |
| L | 0,9 | 3,5 | 0 |
6.3.5. Течение льда по волнообразному ложу. На настоящем этапе был проведен лишь предварительный анализ данных, полученных для куполового ледника Уилкса с позиций теории течения льда по неровностям ложа, изложенной в подразделе 5.4. Основные выводы этого подраздела можно суммировать следующим образом.
1. Неровности ложа вызывают сходные с ними, но демпфированные колебания поверхности ледника.
2. При больших коэффициентах демпфирования вдоль линии тока (φ ≈ 10) колебания поверхности ледника расходятся по фазе с колебаниями основания на величину π/2, так что максимумы наклона поверхности приходятся над максимумами высоты ложа.
3. Поперек линии тока колебания поверхности и ложа совпадают по фазе. Для других направлений течения фазовый сдвиг изменяется от 0 до π/2.
4. Коэффициент демпфирования зависит от толщины льда Z, скорости движения вперед V, параметра вязкости В течения льда и длины волны колебаний λ:
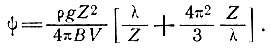
(49)
5. Для данной толщины льда существует характерная длина волны λmin, при которой демпфирование минимально. Это означает, что гораздо более короткие или длинные волны быстрее демпфируются и, как следствие этого поверхностные колебания с длиной волны λ от 2 до 10 раз большей, чем толщина, могут преобладать, хотя, очевидно, могут оказаться также и гармоники λmin
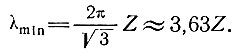
(50)
6. Из детальных измерений высоты поверхности и ложа (или наклонов α2 и β1) значения параметра В закона течения льда можно определить по величинам коэффициента демпфирования, толщине льда и скорости, т. е.
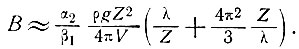
(51)
7. Трехмерные возмущения ложа демпфируются несколько сильнее, чем соответствующие двухмерные.
Для проверки этих выводов требуется точное знание профиля как высоты поверхности, так и высоты ложа, а также величин вектора скорости вдоль линии тока масс льда, предпочтительно с некоторыми данными о векторах скорости поперек линии тока. Идеальным являлось бы знание непрерывных профилей, но на практике обычно приходится довольствоваться их близко стоящими дискретными значениями. В этом случае длины волн, примерно в четыре раза превышающие интервал дискретного расстояния, самые короткие из тех, какие могут быть точно изучены. Дальнейшее ограничение в изучении коротковолновых колебаний заключается в том, что при измерении толщины льда гравитационными методами, сколь бы близко точки измерений ни находились друг от друга, обнаруживается резкое демпфирование волн, длины которых короче, чем несколько толщин льда. Даже радиолокатор выявит демпфирование впадин с меньшей длиной волны, чем критическая величина λкр, если при этом радиус кривизны дна впадины равен толщине льда, т. е. для профиля ложа формы
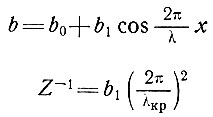
или
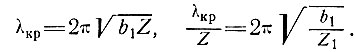
(52)
Имея в виду это ограничение, посмотрим теперь некоторые предварительные данные, относящиеся к куполовому леднику Уилкса.
Д. Картер в 1967 г. получил непрерывные профили ложа этого ледника при помощи радиолокатора относительно трех сторон ADJ северного треугольника ледника (см. рис. 6.9). По результатам радиолокационных измерений на линии DJ профиля наклон поверхности ледника и высота ложа наносились через каждые 1,5 км. Данные о высоте ложа по предшествующим гравитационным и сейсмическим измерениям показаны на рис. 6.10, где наклоны поверхности и высота ложа (величины в точках через 1,5 км) показывают удовлетворительную корреляцию, и поблизости от побережья, где направление течения масс льда близко к этому профилю, они совпадают по фазе.
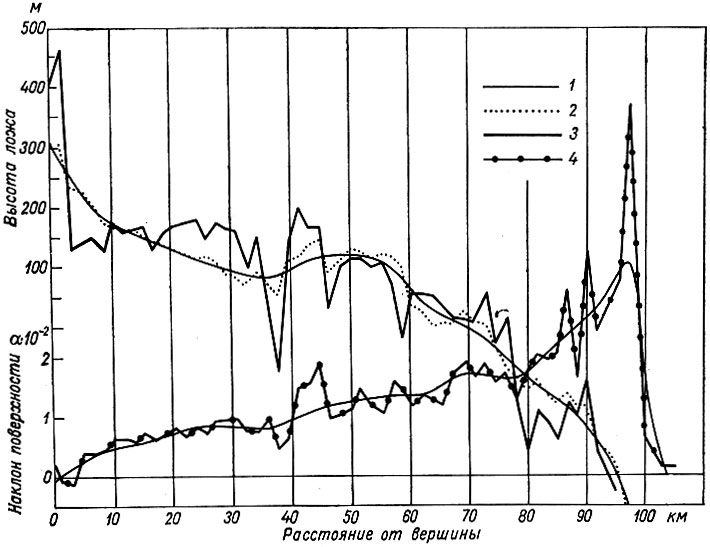
Рис. 6.10. Высота ложа и наклон поверхности куполового ледника Уилкса по линии купол - мыс Пойнсетт. 1 - осреднение через 15 км, 2 - гравитационные (через 1,5 км) и сейсмические (через 15 км) измерения, 3 - радиолокационное зондирование через 1,5 км, 4 - осреднение через 1,5 км
Сразу становится ясно, что хотя между этими двумя профилями имеется хорошее согласование в крупном масштабе, при гравитационных съемках коротковолновые колебания ложа сильно демпфировались.
Отметим следующие качественные моменты.
1. Несмотря на то что размещение точек через каждые 1,5 км не дает возможность проанализировать очень коротковолновые колебания ложа (λ < 5 км), представляется, однако, что доминирующая длина волны колебаний поверхности лежит между 5 и 10 км. Чтобы подтвердить это, потребовались бы подробные знания амплитудно-частотного спектра.
2. Представляется также, что поверхностные колебания все же отражают характер ложа и, как предсказано теорией, наклоны поверхности обычно находятся в одной фазе с высотой ложа. Из анализа рис. 6.9 ясно, что направление действительного течения масс льда отклоняется от линии профиля, особенно в районе решетки деформации G. Это приводит к такому фазовому сдвигу, что наклоны поверхности и ложа имеют расхождение по фазе менее чем на величину π/2.
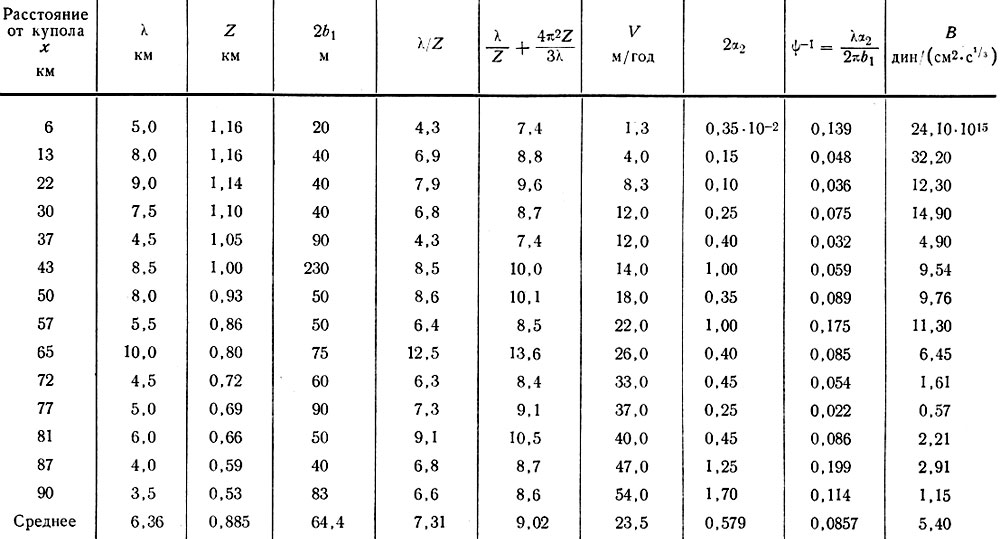
Таблица 6.6
Параметр закона течения В, полученный по коэффициенту демпфирования (формула 51)
3. Большие величины изменения наклона поверхности около побережья показывают, что малое демпфирование соответствует малой толщине льда и большой скорости движения.
Л. Пфитцнер осуществил предварительный количественный анализ этих результатов, основываясь на теории, изложенной в подразделе 5.4, в частности на формуле (51).
В табл. 6.6. представлены величины параметров λ, Z, λ/Z, V, α1, β1, φ, В для доминирующих, как очевидно, волн вдоль заданного направления. На основании этих данных был сделан вывод, что средняя длина волны λ равна 7,31Z. Коэффициент демпфирования (средняя величина φ-1 = 0,086) действительно уменьшался при приближении к побережью.
По этой таблице было рассчитано среднее значение параметра В, равное 5,4 · 1015 дин/(см2 · с1/3). Величина В также уменьшалась по направлению к побережью, как это и ожидалось на основании распределения температур. Это среднее значение В лишь незначительно отличается от значения В, полученного вдоль линии DJ Маклареном [71] по изменению скорости деформации на волнообразном ложе: скорость деформации 5 = 1,5 · 109 дин/(см2 · с1/3), коэффициент демпфирования В = 1,7 · 109 дин/(см2 · с1/3).
Для линии купол - мыс Фольгер (DA) длины волн аналогичны, но скорости оказываются значительно меньше. Коэффициент демпфирования также значительно меньше, и как следствие этого величина параметра В, определенная для этой линии, лишь незначительно отличается от величины параметра В для другой, что подтверждает, таким образом, предыдущие результаты измерений деформации.
Данный анализ лишь предварительный, но он предполагает, что при течении ледника по волнообразной поверхности изменения высоты поверхности и ложа и коэффициенты демпфирования являются ценными характеристиками при исследовании свойств течения ледниковых масс. Более детальный анализ в настоящее время осуществляется Картером, использующим меньшие интервалы между точками измерений (400 м) и проводящим спектральный анализ высоты ложа и поверхности, а также осуществляющим взаимную их корреляцию, что позволит полностью проверить прогнозы течения льда.
|
ПОИСК:
|
© GEOMAN.RU, 2001-2021
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'