6.1. Шельфовые ледники

6.1.1. Общие уравнения движения для определения параметров течения. Общая теория динамики (раздел 5) была применена к шельфовому леднику Эймери Баддом [16], который показал, как можно ее использовать для определения параметров течения льда по измерениям скорости движения ледника и скорости деформации с учетом профиля высоты.

Основные принципы применения этой теории в общих чертах описаны ниже. Если для многих шельфовых ледников диапазон напряжений относительно небольшой (0 - ³/₄ бара), то можно использовать параметры В, п для вывода степенного закона течения льда и получить средние величины в этом диапазоне. После того как определены величины п и В, можно рассчитать распределение скорости по всей остальной части шельфового ледника.

Рассмотрим общее уравнение скорости продольной деформации 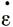_х на расстоянии х вдоль центральной линии шельфового ледника (см. раздел 5, уравнения (31а) подраздела 5.1, (17) подраздела 5.2, (29) подраздела 5.3), причем членом 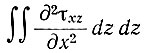пренебрегаем, поскольку рассматриваем здесь не коротковолновые флуктуации наклона, а средние значения параметров на больших расстояниях:

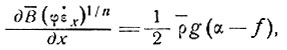
(1)

где В - среднее значение параметра течения по толщине льда, φ - функция поперечной деформации (см. уравнение (27) раздела 5), α - продольный наклон поверхности, осредненный поперек шельфового ледника в положении х и f - коэффициент трения на границе ледника, определяемый как

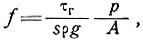
(2)

где τ_г - напряжение сдвига на границе, р/А - отношение граничного периметра поперечного сечения к площади и s - соответствующий коэффициент форм поперечного сечения.

Для шельфового ледника коэффициент s равен единице, как для бесконечно глубокого канала, поскольку у основания ледника напряжения сдвига отсутствуют.

Пусть σ_х будет продольное напряжение и хху - поперечное напряжение сдвига в положении х вдоль шельфового ледника и на расстоянии у от центральной линии. Допустим сначала, что 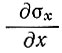не зависит от у. Из условия равновесия для какого-либо центрального элемента получаем

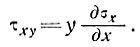
Отсюда при степенном законе течения с параметрами n и В градиент скорости поперек шельфового ледника определяется как

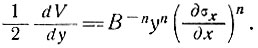
Если половина ширины шельфового ледника равна а, то скорость в центре V (см. п. 3.4.1) составит

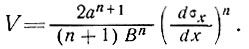
(3)

Выражение напряжения сдвига у края имеет вид

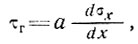
(4)

или, согласно выражению (3),

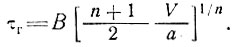
(5)

Эту величину τ_г теперь можно подставить в уравнения (2) и (1), и учитывая, что для такого шельфового ледника р/Л = 1/а, имеем

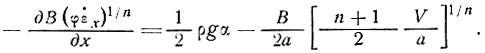
(6)

Отсюда, если в дополнение к размерам шельфового ледника известны параметры течения n и В, так же как и некоторые граничные значения скорости движения и скорости деформации, то уравнение (6) можно решить методом итераций, в результате чего и были получены величины скорости движения и деформации вдоль центральной линии течения [заметим, что здесь вносится поправка в уравнение (7) Бадда [16] в том смысле, что вместо градиента 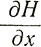толщины который применим лишь при наклоне основания β = 0, используется наклон поверхности α]. С другой стороны, если скорость вдоль центральной линии течения известна, уравнение (6) позволяет рассчитать параметры течения. Вообще, значения параметров n и В приходится определять из численных решений уравнения (6), за исключением тех случаев, когда особые формы граничных условий позволяют ввести упрощения. Эти особые случаи и будут сейчас рассмотрены.

6.1.2. Особые случаи распределения скорости. Для трех особых случаев Бадд [16, 17] показал, что можно получить аналитические решения. Рассмотрим случай шельфового ледника, ограниченного с боков, имеющего ширину 2а, причем параметры течения n и В и коэффициент поперечной деформации φ медленно изменяются вдоль ледника.

Для удобства дальнейшего изложения изменим направление оси х, т. е. ось х расположим горизонтально вдоль центральной линии, направленной внутрь материка от фронта ледника, обращенного к морю.

Уравнение (6) можно записать теперь следующим образом:

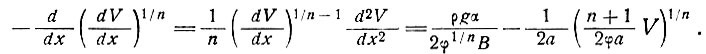
Случай I. Плоский шельфовый ледник (а → 0).

Здесь уравнение (6) сводится к

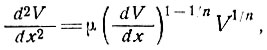
(7)

где

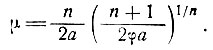
(8)

Это выражение имеет решение для частного случая V = 0, когда 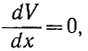, а именно,

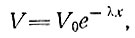
(9)

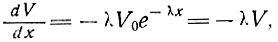
(10)

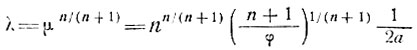
(11)

и V₀ - скорость движения шельфового ледника у его фронта (х = 0). Этот результат означает, что как скорость движения, так и скорость продольной деформации в плоском шельфовом леднике уменьшаются экспоненциально при движении в глубь материка от фронта ледника, причем величина этого уменьшения зависит от индекса n, ширины ледника и скорости поперечной деформации.

В более общем случае, когда V = Vo при 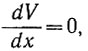интегрировать труднее; тогда находим следующее соотношение между скоростью продольной деформации и скоростью движения:

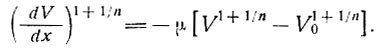
Его также можно использовать для определения величины n по измеренному профилю скорости вдоль центральной линии.

Случай II. При постоянной вязкости (n = 1).

Имеем n = 1 в уравнении (6):

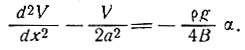
(12)

В этом случае получаем для постоянного наклона поверхности α и условия

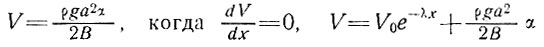
(13)

и видим, что результирующая скорость есть простая сумма скоростей, обусловленных ползучестью и градиентом давления, действующими независимо друг от друга.

Здесь опять скорость движения ледника и ее градиент уменьшаются экспоненциально при удалении от фронта шельфового ледника в глубь материка до тех пор, пока скорость деформации не обратится в нуль при 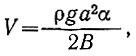как и ожидается при нормальном вязком течении без продольной деформации. В этом случае экспоненциальное уменьшение управляется по закону 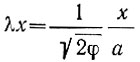и зависит от ширины шельфового ледника.

Случай III. Для сравнительно плоского шельфового ледника, где наклон медленно меняется вдоль центральной линии, можно использовать следующие приближенные решения.

Запишем суммарную скорость в положении х в виде

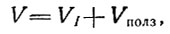
(14)

где V₁ - скорость, определяемая одним градиентом давления, и V_полз - градиент скорости вследствие изменяющейся ползучести. Теперь, если

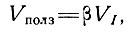
(15)

то для области в направлении фронта шельфового ледника, где β изменяется медленно вдоль ледника, получаем уравнение

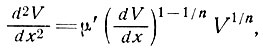
(16)

где

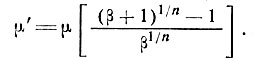
Теперь решение может быть записано в виде

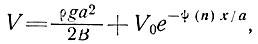
(18)

где

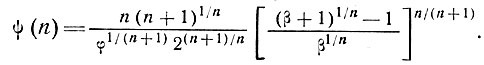
(19)

Эта функция графически представлена Баддом ([16, рис. 10], где φ обозначена через коэффициент φ), при коэффициенте поперечной деформации φ = 1.

Точное решение для скорости деформации 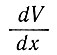в величинах скорости V в этом случае имеет вид

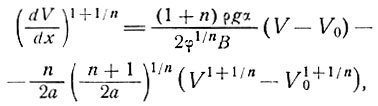
где V = V₀, когда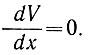

Далее, если параметры α, В, а медленно изменяются с изменением расстояния х, то значения n можно получить из второго члена правой части уравнения (18), которое управляет экспоненциальным уменьшением скорости при движении в глубь материка от фронта ледника. Для районов далеко в глубине материка этот член уменьшается до нуля. Тогда значение В можно легко определить по скорости движения, наклону, толщине и ширине шельфового ледника. Значение n = 2 было найдено Баддом [16] в результате численного решения уравнения (18) применительно к шельфовому леднику Эймери. После введения поправок на наклон основания, как упоминалось ранее, значение В = 0,63 × 10⁹ дин/(см² ·с^1/₃).

Это значение представляется несколько более низким, чем ожидаемое (≈ 1,3·10⁹) из закона течения (см. рис. 2.2) при -16° С, т. е. средней температуре, рассчитанной для этой области шельфового ледника. Низкое значение В может быть результатом малой плотности льда (ρ≈0,85 г/см³), что в соответствии с п. 2.5.1 могло бы привести к тому, что значение В (в этих же единицах) было бы меньше примерно в 1,6 раза. Однако вследствие неточностей в предварительных данных, имеющихся по шельфовому леднику Эймери, полученных ранее, нельзя ожидать более точного согласования. На данном этапе проекта "Шельфовый Ледник Эймери" ставится целью получение достаточного количества данных для полного анализа детальным измерением толщины льда и распределений скорости, а с помощью бурения получение информации о профилях температуры и об изменениях плотности с глубиной.