2.4. Влияние температуры на закон течения льда

Результаты измерений скорости деформации как функции от температуры при различных напряжениях сдвига, заимствованные из работ Меллора и Смита [80], Бутковича и Ландауэра [21], Штайнемана [130] и Войтковского [136], отражены на рис. 2.4.

Для выражения зависимости скорости деформации от температуры некоторые предыдущие авторы использовали отношение вида

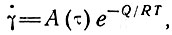
(15)

где А (τ) - функция, зависящая от напряжения при постоянной температуре; Q - энергия активации (кал/моль); R - газовая постоянная, равная примерно 1,90 кал/(моль•К); Т - абсолютная температура (К).

Для малых напряжений (0,5 - 1 бар) Меллор и Смит определили, что Q ≈ 10÷12 ккал/моль, а Буткович и Ландауэр - Q ≈ 14 ккал/моль.

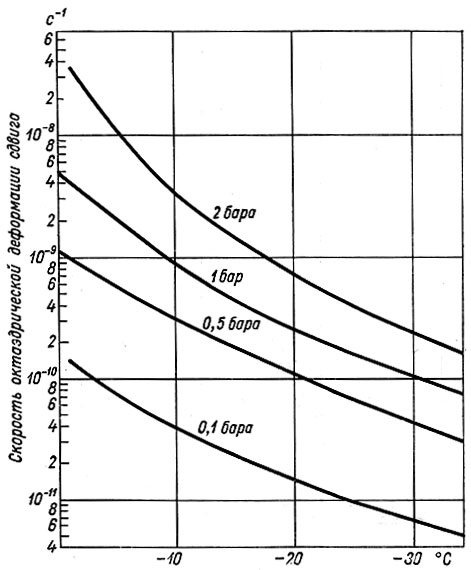
Рис. 2.4. Зависимость скорости октаэдрической деформации сдвига льда от его температуры при различных напряжениях (логарифмическая шкала). Графики составлены и интерполированы по данным рис. 2.2

Результаты Штайнемана [ 130] и Глена [34] предполагают, что при более высоких напряжениях и скоростях деформации Q может приобретать большие значения. Меллор и Смит [80] указывали, что функция Аррениуса ехр(-Q/RT) не имеет отношения к диапазону температур, встречающихся в естественных массах льда. Эти наблюдения проще представить эмпирическим законом вида

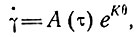
(16)

где К - константа, а θ - температура (°С).

По данным Меллора и Смита [80] (τ = 0,5÷1 бар), K ≈ ¹/₁₁, а Бутковича и Ландауэра [21] K ≈ ¹/₉. По данным Штайнемана (1958), при больших напряжениях (≈2 бара) K = ¹/₆. Войтковский [136] утверждает, что уравнение (15) не пригодно для того, чтобы представить зависимость закона течения льда от температуры, потому что оно не согласуется со значительным возрастанием скорости деформации по мере приближения температуры льда к точке замерзания, которое он получил в результате своих экспериментов.

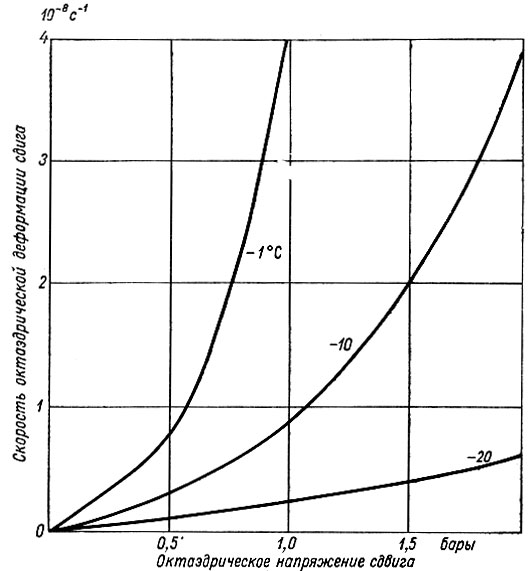
Рис. 2.5. Зависимость скорости октаэдрической деформации сдвига льда от октаэдрического напряжения сдвига в линейных координатах при различных температурах. Составлено по данным рис. 2.2

Более справедливым Войтковский нашел следующее отношение:

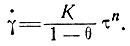
(17)

Здесь n - константа, составляющая примерно 1,6 - 2,2 в диапазоне напряжений 0,1 - 3 бара, а K = (1,6 - 4) o 10⁵ °С/Кг/ч. Результаты Войтковского до температуры льда -40° С можно также аппроксимировать выражением (16). В этом случае K ≈ ¹/₁₀. Эта зависимость хорошо согласуется с экспериментальной при низких температурах льда, но по мере приближения последних к нулю измеренная скорость деформации возрастает.

В ожидании более точных данных примем, что любая из функций (15), (16) или (17) представляет зависимость закона течения льда от его температуры, и при соответственно выбранных величинах, постоянных в данном температурном диапазоне, можно ожидать удовлетворительного согласия с экспериментом при условии, что экстраполяция произведена вблизи от рассматриваемого диапазона.

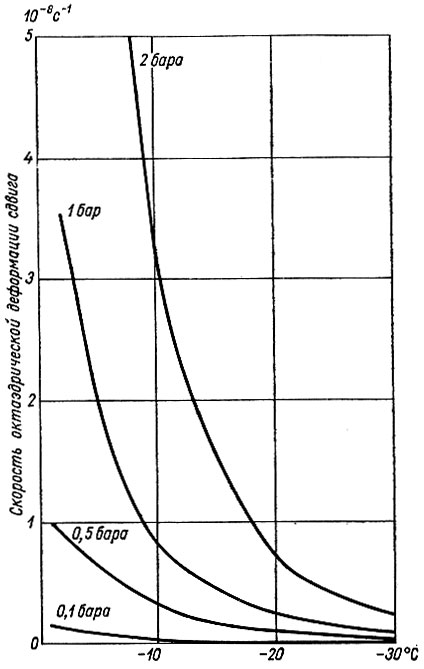
Рис. 2.6. Зависимость скорости октаэдрической деформации сдвига льда от его температуры в линейных координатах при различных напряжениях (бары). Составлено по данным рис. 2.2

Для иллюстрации быстрых изменений скорости деформации льда с изменением температуры и напряжения сдвига льда обратимся к графикам линейной зависимости скорости деформации от напряжения (рис. 2.5) и скорости деформации от температуры (рис. 2.6). На рис. 2.5 и 2.6 видно, что скорость деформации сдвига становится очень высокой по мере того, как напряжение возрастает выше величины 0,5 бара,, а температура приближается к нулю. Исходя из этого, неудивительно, что в естественно деформирующемся льду напряжение сдвига обычно не превышает 1 бара, за исключением тех случаев, когда температура очень низка.