
§ 2.3 Искажения в картографических проекциях; их распределение; определение размеров искажений на картах
Искажение (деформация) изображения, выражающееся в изменениях масштаба длин, присуще всем картографическим проекциям, - это их основное свойство. Но проекции различаются по характеру искажений (равноугольные, равновеликие, равнопромежуточные произвольные), по величине искажений и их распределению. Вообще говоря, проекции могут иметь отдельные точки, линии или даже систему линии, где сохраняется главный масштаб. В азимутальных проекциях - это точка касания плоскости, в конических - параллель касания конуса (или параллели сечения) и т. п. Такие точки и линии называются точками и линиями нулевых искажений. Искажения возрастают по мере удаления от точек или линий нулевых искажении. Другими словами, они возрастают с увеличением размеров картографируемой территории.
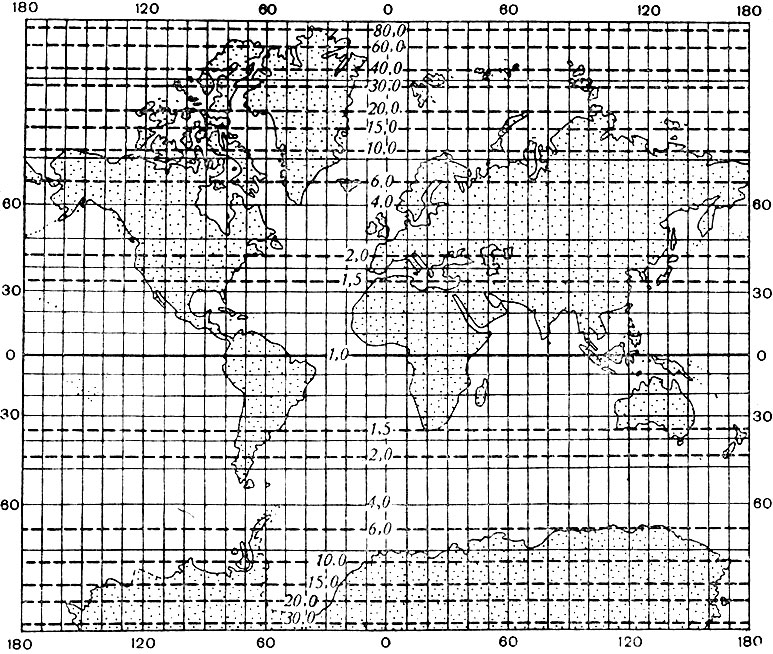
Рис. 2.13. Изоколы площадей в равноугольной цилиндрической проекции Меркатора
Для оценки достоинств проекции используют показатели искажения площадей р и углов ω, определяемые при вычислении проекции. Определение этих величин для ряда точек картографической сетки и последующее проведение по ним изокол - линий, соединяющих точки с одинаковыми значениями искажений площадей и углов, дает наглядную картину распределения искажений и позволяет учитывать искажения при пользовании картой.
В нормальных цилиндрических проекциях (рис. 2.13) изоколы располагаются параллельно экватору (или параллелям сечения); в нормальных конических проекциях - параллельно параллели касания (или параллелям сечения); в нормальных азимутальных проекциях изоколы параллельны концентрическим окружностям параллелей. Очевидно, нормальные цилиндрические проекции целесообразно применять для изображения экваториальной зоны и вообще территорий, вытянутых вдоль экватора; нормальные конические проекции - для территорий, лежащих в средних широтах и вытянутых с востока на запад (например, для СССР); нормальные азимутальные проекции - для полярных районов.
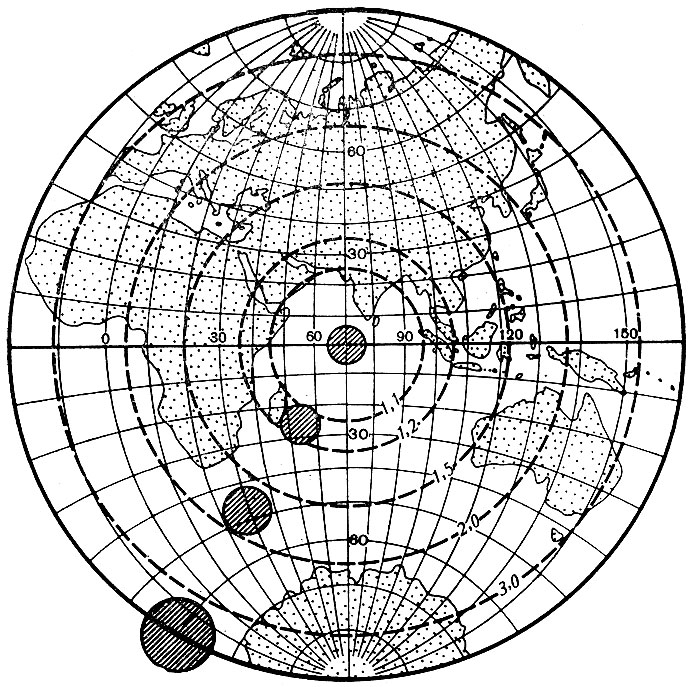
Рис. 2.14. Картографическая сетка в экваториальной стереографической проекции с изоколами площадей
Также легко представить расположение изокол в поперечных и косых проекциях. Например, в поперечной цилиндрической проекции изоколы параллельны меридиану касания, и, следовательно, такие проекции выгодны для передачи территорий, вытянутых вдоль этого меридиана с севера на юг. В любой азимутальной проекции изоколы образуют окружности, концентрические относительно точки касания плоскости (рис. 2.14 и 2.15); поэтому азимутальные проекции удобны для территорий округлой формы (при центральном положении точки касания). В произвольных проекциях изоколы могут образовывать сложную систему кривых линий (см. рис. 2.8). В математической картографии доказывается, что при изображении конкретных территорий наименьшие искажения обеспечиваются проекциями, у которых изоколы по своей форме близки к общему контуру картографируемой территории.
Важно знать, что при наличии картографической сетки величина искажений может быть определена на любом участке карты, еслв даже проекция не указана.
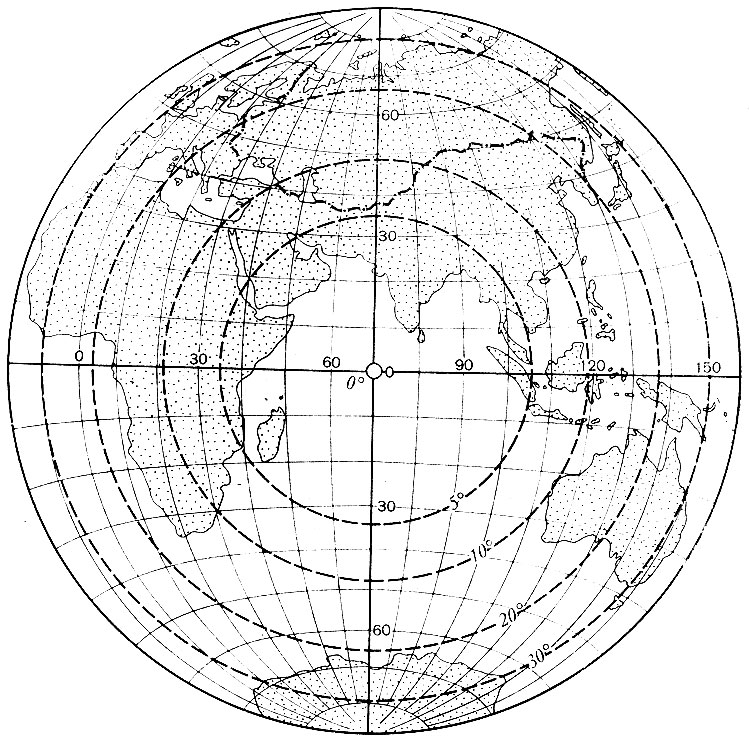
Рис. 2.15. Картографическая сетка в экваториальной равновеликой азимутальной проекции (Ламберта) с изоколами углов
Для этого достаточно определить в соотвествующем месте карты масштабы по меридиану и параллели т и п, а также угол θ между меридианом и параллелью. Для нахождения величин т и п следует: а) измерить дуги меридиана и параллели возле соответствующей узловой точки картографической сетки; б) определить масштаб по меридиану и параллели посредством деления полученных величин на длины соответствующих дуг эллипсоида (заимствуемые из картографических таблиц). Найти величины т и п посредством деления масштабов по меридиану и параллели на главный масштаб. Угол θ между меридианом и параллелью измеряется транспортиром.
Для вычисления по величинам т, п и углу θ значений а, b, р, и угла θ математическая картография дает следующие несложные формулы:
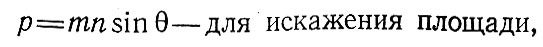
(2.4)
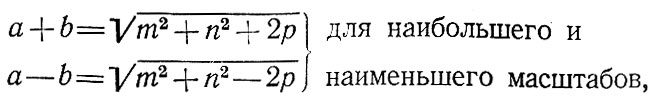
(2.5), (2.6)
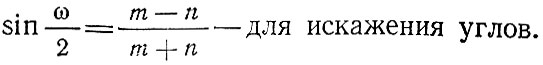
(2.7)
Если главные направления совпадают с меридианами и параллелями, т. е. когда меридианы и параллели сетки взаимно перпендикулярны, то а=т, b=п (или а=п, b=т) и формулы приобретают вид
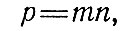
(2.8)
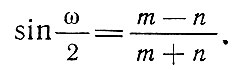
(2.9)
|
ПОИСК:
|
© GEOMAN.RU, 2001-2021
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'
При использовании материалов проекта обязательна установка активной ссылки:
http://geoman.ru/ 'Физическая география'