Глава 2. Математическая основа карт

§ 2.1 Понятие о картографических проекциях. Классификация проекций по характеру искажений

При переходе от физической поверхности Земли к ее отображению на плоскости (на карте) выполняют две операции: проектирование земной поверхности с ее сложным рельефом на поверхность земного эллипсоида, размеры которого установлены посредством геодезических и астрономических измерений, и изображение поверхности эллипсоида на плоскости посредством одной из картографических проекций.

Картографическая проекция - математически определенный способ отображения поверхности эллипсоида на плоскости - устанавливает однозначное соответствие между точками земного эллипсоида и изображениями тех же точек на плоскости. Обычно это соответствие выражают в аналитической форме в двух уравнениях вида

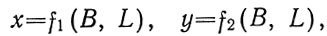
(2.1)

называемых уравнениями картографических проекций. Они позволяют вычислять прямоугольные координаты х, у изображаемой точки по географическим координатам В и L. Число возможных функциональных зависимостей и, следовательно, проекций неограниченно. Необходимо лишь, чтобы каждая точка В, L эллипсоида изображалась на плоскости однозначно соответствующей точкой х, у и чтобы изображение было непрерывным.

Поверхность эллипсоида (или шара) нельзя развернуть на плоскости подобно поверхности конуса или цилиндра. Поэтому непрерывность и однозначность изображения достигаются как бы за счет неравномерного растяжения (или сжатия), т. е. деформации поверхности эллипсоида при совмещении ее с плоскостью. Отсюда следует, что масштаб плоского изображения не может быть постоянным. Для наглядного представления о величине и характере деформаций, свойственных определенной проекции, рассматривают, как изображаются на плоскости бесконечно малые окружности, взятые в разных точках на поверхности эллипсоида. В теории картографических проекций доказывается, что бесконечно малая окружность на поверхности эллипсоида в общем случае изображается на плоскости эллипсом, называемым эллипсом искажений. Это означает, что масштаб изображения зависит не только от положения точки, но может изменяться в данной точке с переменой направления. Эллипс искажений характеризует для этой точки величины искажений длин, площадей и углов.

Различают главный масштаб dS, равный масштабу модели земного эллипсоида, уменьшенного в заданном отношении для изображения на плоскости, и прочие масштабы, называемые частными. Частный масштаб dS^,определяется как отношение бесконечно малого отрезка на карте (на плоскости) к соответствующему ему отрезку на поверхности эллипсоида. Отношение частного масштаба к главному, обозначаемое через μ, характеризует искажение длин

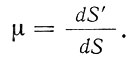
(2.2)

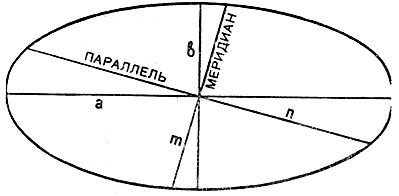
Рис. 2.1. Эллипс искажений и его элементы

В любой точке на поверхности эллипсоида имеются два взаимно перпендикулярных направления (называемых главными), которые в проекции также изображаются взаимно перпендикулярными линиями, совпадающими с большой и малой осями эллипса искажения (рис. 2.1). Очевидно, в эллипсе искажений наибольший масштаб совпадает с направлением большой оси эллипса, а наименьший с направлением малой оси. Экстремальные масштабы по главным направлениям, выраженные в отношении к главному масштабу, обозначают соответственно через а и b. Вообще, главные направления могут не совпадать с меридианами и параллелями (и их изображением в проекции). В таком случае масштабы по меридиану и параллели обозначают соответственно через т и п.

Непостоянство масштабов в данной точке по разным направлениям можно видеть на рис. 2.2, б, где длины изображаемых меридианов равны длинам меридианов эллипсоида (разумеется, с уменьшением до масштаба карты), а длины параллелей увеличиваются по мере удаления от экватора. На рисунке отрезки параллелей между двумя меридианами одинаковы на любой широте, тогда как в действительности они уменьшаются с приближением к полюсу до нуля. Таким образом, масштаб вдоль меридианов постоянен в любой точке карты, но вдоль параллелей он возрастает с увеличением широты. Это видно по эллипсам искажений, показанным на рис. 2.2, б.

Наряду с искажениями длин различают искажения площадей и углов. За искажение площади в некоторой точке карты принимают отношение площади эллипса искажений dP^, к площади dP соответствующего бесконечно малого круга на эллипсоиде, обозначаемое через р:

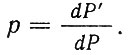
(2.3)

Искажением угла называют разность между углом, образованным двумя линиями на эллипсоиде, и изображением этого угла на карте. Величина искажения углов в данной точке характеризуется наибольшим значением этой разности ω.

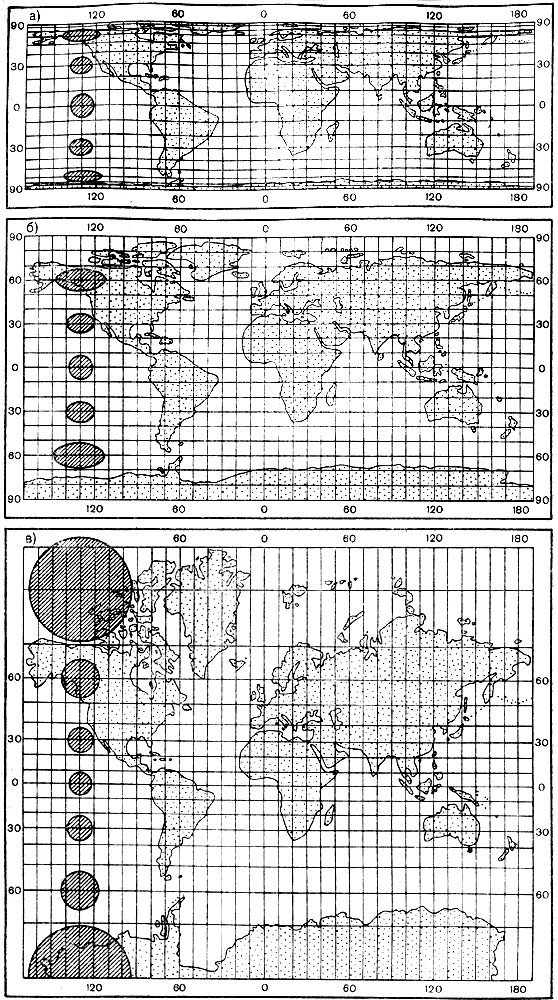
Рис. 2.2. Картографические сетки в цилиндрических проекциях: а - равновеликой; б - равнопромежуточной; в - равноугольной (Меркатора)

Проекций, совершенно лишенных искажений длин, не существует. Такие проекции сохраняли бы подобие и пропорциональность всех частей земной поверхности, что может иметь место только на модели эллипсоида. Вместе с тем есть проекции, свободные от искажения углов или от искажений площадей.

Проекции, которые передают величину углов без искажения и сохраняют подобие бесконечно малых фигур, называются равноугольными. Одна из них изображена на рис. 2.2, в. В каждой точке равноугольной проекции масштаб одинаков на всех направлениях (эллипс искажений превращается в окружность), но меняется от точки к точке. Это видно по изменению размеров окружностей - эллипсов искажений.

Равновеликие проекции сохраняют площади (эллипсы искажений везде имеют одинаковую площадь), но сильно нарушают подобие фигур (вытянутость эллипсов искажений различна) (см. рис. 2.2, а).

Существует множество проекций, которые не являются ни равноугольными, ни равновеликими, - их называют произвольными. Но нет и не может быть проекции, которая была бы одновременно равноугольной и равновеликой. Вообще, чем больше искажения углов, тем меньше искажения площадей и наоборот. Среди произвольных проекций выделяют равнопромежуточные, во всех точках которых масштаб по одному из главных направлений постоянен и равен главному масштабу (например, по меридианам или параллелям в проекциях, где они совпадают с главными направлениями). По своим свойствам произвольные проекции лежат между равноугольными и равновеликими.

Характер искажений, присущий проекции (равноугольная, равновеликая, равнопромежуточная), отмечается в ее названии.