КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ

Расстановка ударений: КАРТОГРАФИ`ЧЕСКИЕ ПРОЕ`КЦИИ

КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ математич. способы изображения на плоскости всей или части земной поверхности,принимаемой за поверхность шара или эллипсоида вращения. Картографич. проекцией часто называют также картографич. сетку, показываемую на картах и изображающую сеть меридианов и параллелей шара или эллипсоида на плоскости в какой-либо К. п. Поскольку поверхности шара и эллипсоида нельзя без складок и разрывов развернуть на плоскости, их изображения на плоскости имеют искажения длин, площадей и углов (не обязательно все одновременно: в различных группах К. п. отдельные искажения могут быть исключены). Масштаб карты, называемый частным масштабом и определяемый как отношение бесконечно малой дуги на шаре (эллипсоиде) и соответствующего отрезка на плоскости (карте), в отличие от масштаба плана, различен в разных точках и, кроме того, может меняться в зависимости от выбранного направления на карте. На картах обычно подписываются общий или главный масштаб, представляющий собой степень уменьшения шара или эллипсоида при их изображении на плоскости. Математич. основой карт и способами учёта влияния свойственных К. п. искажений занимается математич. картография.

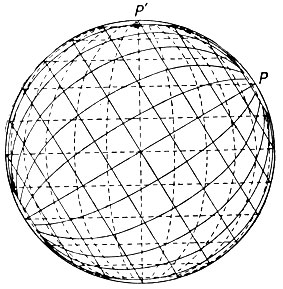
1. СЕТИ СФЕРИЧЕСКИХ КООРДИНАТНЫХ ЛИНИЙ. Сплошными линиями показаны меридианы и параллели, пунктирными - вертикалы и альмукантараты

Изображение поверхности шара или эллипсоида на плоскости (карте) производится с помощью меридианов и параллелей или аналогичных им сферич. координатных линий - вертикалов и альмукантаратов (см. рис. 1), на основе к-рых получаются нормальная, поперечная и косая системы координат и им соответствующие проекции: нормальная, или полярная (см. табл. 1 - рис. 1; II - рис. 1, 2; III - рис. 1, 2; IV - рис. 1; V - рис. 1; VI - рис. 1, 2); поперечная, или экваториальная (см. табл. I - рис. 2; II - рис. 3); косая, или горизонтальная(см. табл. I - рис. 3; II - рис. 4). К. п. классифицируется по двум основным признакам - по характеру искажений (свойству изображения) и по виду меридианов и параллелей нормальной сетки. По характеру искажений К. п. бывают: равноугольные (конформные), не искажающие углов; равновеликие (эквивалентные), сохраняющие площади фигур; равнопромежуточные (эквидистантные), во всех точках которых масштаб по одному из главных направлений равен общему масштабу; произвольные, не обладающие ни одним из свойств названных проекций. Для характеристики К. п. используются изоколы - линии одинаковых искажений; изображения нек-рых линий положения - ортодромии и локсодромии (в табл. II, рис. 1 - О - ортодромия и Л - локсодромия), а также нек-рые др. способы. По виду меридианов и параллелей нормальной сетки различаются след, проекпии. Азимутальные проекции (назывались ранее также зенитальными), в к-рых параллели - кбн-центрич. окружности, а меридианы- радиусы этих окружностей, при этом углы между меридианами соответствуют разностям долгот (см. табл. I). Перспективные проекции, являющиеся частным случаем азимутальных, получаются путём проектирования земной поверхности, обычно принимаемой за поверхность шара, на картинную плоскость К прямыми О А, выходящими из одной точки О, причём картинная плоскость перпендикулярна прямой ОС, проводящей через центр Земли (см. рис. 2).

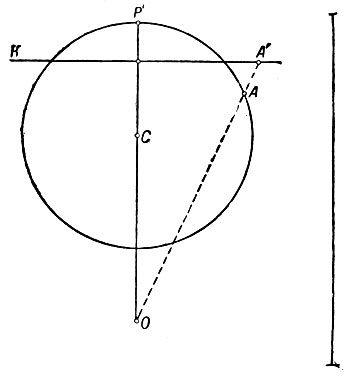
2. ПЕРСПЕКТИВА ШАРА. НА ПЛОСКОСТЬ. Картинная плоскость К может быть секущей сферу по данному альмукантарату или касательной в точке Р

В зависимости от расстояния Д, от точки проектирования О до центра сферы С, перспективные проекции подразделяются на ортографические при Д=оо, стереографические при Д=Д, центральные при Д = 0 и внешние при Д>R, где Д - радиус шара. Цилиндрические проекции, в которых параллели - параллельные прямые, а меридианы - перпендикулярные им равноотстоящие прямые (см. табл. 11). Проекция Гаусса (Гаусса - Крюгера), представляющая собой равноугольную поперечно-цилиндрич. К. п. земного эллипсоида, применяется в СССР и др. странах при составлении топографич. карт и обработке триангуляции. Конические проекции, в к-рых параллели - дуги концентрических окружностей, а меридианы - их радиусы; углы между меридианами пропорциональны разностям долгот (см. табл. III). В псевдоцилиндрических проекциях параллели - параллельные прямые, а меридианы - кривые, симметричные относительно среднего прямолинейного меридиана (см. табл. IV). В псевдоконических проекциях параллели - дуги концентрич. окружностей, а меридианы-кривые, симметричные относительно среднего прямолинейного меридиана (см. табл. V). П оликоническими наз. К. п., параллели к-рых являются дугами эксцентрич. окружностей, а меридианы - кривыми, симметричными относительно среднего прямолинейного меридиана, при этом центры параллелей располагаются на продолжении среднего меридиана (см. табл. VI). Видоизменённая простая полико-нич. проекция (см. табл. VI - рис. 1) применяется как многогранная трапеция по широте 4° и по долготе 6° в СССР и мн. др. странах мира для карты масштаба 1:1000000. Еcли при изображении поверхности эллипсоида её разбивают на части - трапеции определённых размеров - и каждую трапецию изображают отдельно, то говорят, что проекция применяется как многогранная; проекцию же иногда называют многогранной.

Выбор проекции той или иной карты обусловлен назначением карты, содержанием, масштабом, а также характером её использования.

Для мелкомасштабных геогр. карт применяются весьма разнообразные К. п. Так, напр., для следующих основных видов карт наиболее целесообразными и часто применяемыми К. п. являются: для карт областей, отдельных союзных республик и отдельных государств - равноугольная и равнопромежуточная конические; для карт СССР - те же конические, косые перспективно-цилиндрич. и произвольные поликонич. и иногда псевдоконические; для карт материков - равновеликие косые азимутальные (для карт Африки - поперечная); для карт океанов - равновеликие и иногда произвольные псевдоцилиндрич., а также произвольные поликонич.; для карт полушарий - северного и южного - полярная равнопромежуточная азимутальная; для карт полушарий - западного и восточного - равновеликая , поперечная азимутальная; для карт мира - произвольные поликонич., псевдоцилиндрич. и цилиндрич., иногда проекция Меркатора.

Спец. карты составляются или в тех же проекциях, что и общегеографич. карты, служащие для них основой, напр, многие спец. карты масштаба 1:1000000, карты СССР, карты мира и др., или в проекциях, наиболее целесообразных для спец. карт, напр, морские карты - в проекции Меркатора, на к-рой локсодромии - прямые линии; маршрутные аэронавигационные карты - в косой меркаторской; аэронавигационные площадные карты - в видоизменённой простой поликонической.

Лит.: Каврайский В. В., Избранные труды, т. 2 - Математическая картография, вып. 1 - 2, М., 1958 - 1959; Урмаев Н. А., Математическая картография, М., 1941; Соловьев М. Д., Картографические проекции, М., 1946; Урмаев Н. А., Исследования по математической картографии, М., 1953 (Труды ЦНИИГАиК, вып. 98); Гинзбург Г. А., Карпов Н. Е. и Салманов а Т. Д., Математическая картография в СССР, М., 1955 (Труды ЦНИИГАиК, вып. 99). Ф. А. Старостин.

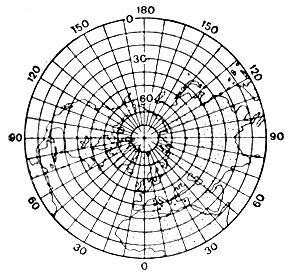
1. Полярная равнопромежуточная. Длины сохраняются вдоль меридианов, а также в точке касания плоскости (в полюсе) или вдоль западной параллели

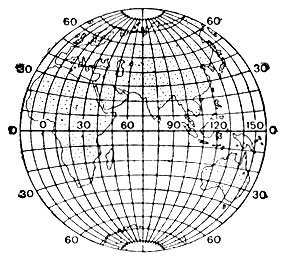
2. Поперечная равновеликая. Длины сохраняются в центральной точке - точке касания плоскости (на экваторе) или на заданном малом круге - альмукантарате

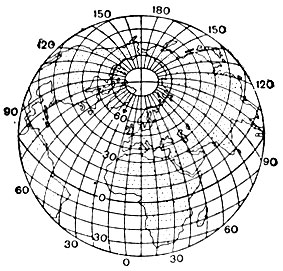
3. Косая равнопромежуточная. Длины сохраняются вдоль больших кругов - вертикалов, а также в точке касания плоскости или вдоль заданного малого круга - альмукантарата

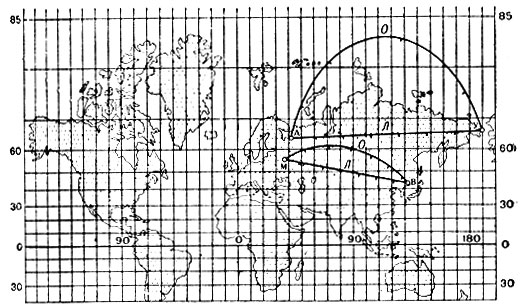
1. Равноугольная Меркатора. Длины сохраняются на экваторе (касательный цилиндр) или на двух данных параллелях (секущий цилиндр)

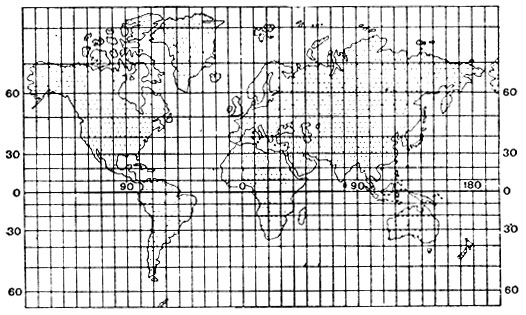
2. Произвольная Н. А. Урмаева, полученная численными методами. Длины сохраняются на экваторе или на двух данных параллелях

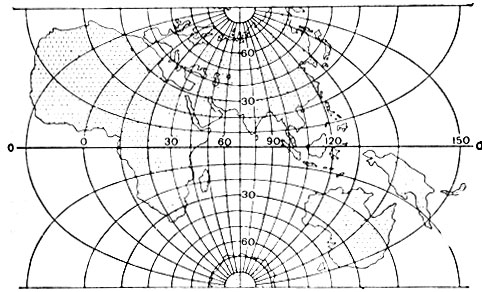
3. Поперечная равноугольная. Длины сохраняются вдоль среднего меридиана (поперечный касательный цилиндр) или двух малых кругов - альмукантаратов (поперечный секущий цилиндр)

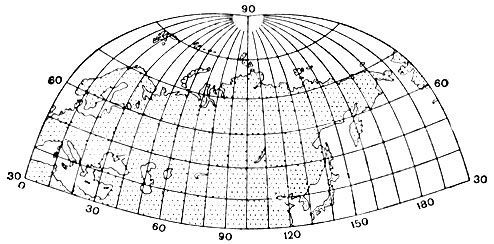
4. Косая перспективно-цилиндрическая М. Д. Соловьева. Длины сохраняются по малому кругу - альмукантарату (косой секущий цилиндр)

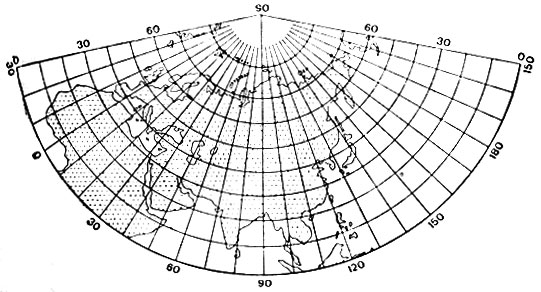
1. Равноугольная Ламберта. Длины сохраняются на одной параллели (касательный конус) или на двух параллелях (секущий конус), называемых стандартными

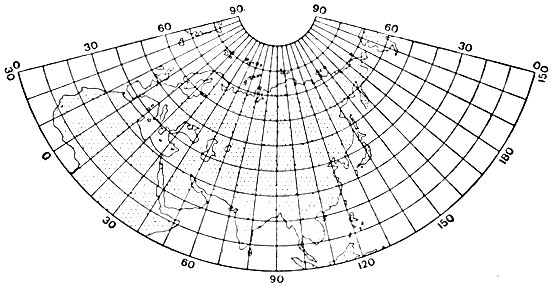
2. Равнопромежуточная В. В. Каврайского. Длины сохраняются вдоль меридианов и параллелей с широтами φ><sub>1</sub> = 47° и φ<sub>2</sub> = 62°

2. Равнопромежуточная В. В. Каврайского. Длины сохраняются вдоль меридианов и параллелей с широтами φ₁ = 47° и φ₂ = 62°

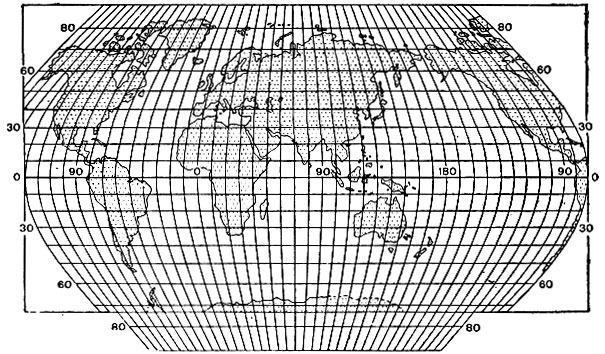
Произвольная ЦНИИГАиК с неравнораздельными параллелями. Длины сохраняются на всех меридианах в точках с широтой φ><sub>0</sub> = 0°

Произвольная ЦНИИГАиК с неравнораздельными параллелями. Длины сохраняются на всех меридианах в точках с широтой φ₀ = 0°

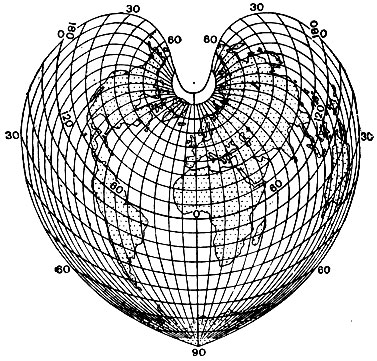
Равновеликая Бонна. Длины сохраняются вдоль среднего меридиана и параллелей

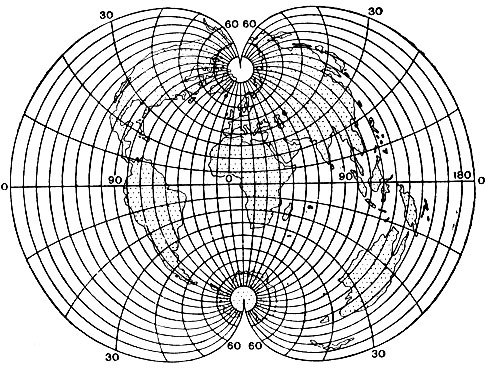
1. Простая. Длины сохраняются вдоль среднего меридиана и параллелей

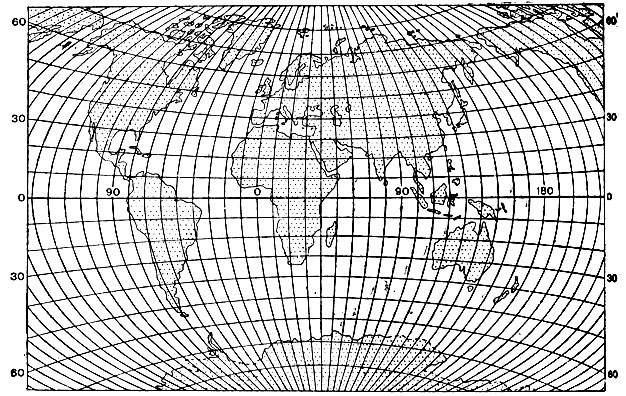
2. Произвольная Г. А. Гинзбурга. Длины сохраняются вдоль двух параллелей с широтами φ><sub>0</sub> = ±45° Проекция применима для карт мира БСЭ и МСЭ

2. Произвольная Г. А. Гинзбурга. Длины сохраняются вдоль двух параллелей с широтами φ₀ = ±45° Проекция применима для карт мира БСЭ и МСЭ