МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИЧЕСКОЙ ГЕОГРАФИИ

Расстановка ударений: МАТЕМАТИ`ЧЕСКИЕ МЕ`ТОДЫ В ЭКОНОМИ`ЧЕСКОЙ ГЕОГРА`ФИИ

МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИЧЕСКОЙ ГЕОГРАФИИ — применение математических паук, включая математическую статистику, математич. логику, теорию информации и общую теорию динамических систем, а также счетно-решающих устройств (электронно-вычислительных машин—ЭВМ) для решения теорстнч. и прикладных проблем экономич. географии. К осн. задачам М. м. относятся: а) выявление закономерностей территориальной структуры х-ва и расселения, их выражение в форме корреляционных или функциональных зависимостей между; показателями; б) оптимизация, на основе этих закономерностей, плановых и проектных решений по территориальной организации хоз-ва.

Применение М. м. в э. г. включает построение математич. моделей экономнко-географич. явлений и процессов, т. е. теоретически обоснованного, масштабно-подобного и структурно эквивалентного отображения их с помощью системы величин (параметров) определенной размерности и структуры.

Элементами модели могут быть величины разных типов (скаляры, векторы, матрицы и т. д.) и связи между ними (функции, операторы). Моделирование включает установление правил и приёмов для перевода исходных данных (фактов, цифровых данных, графиков и карт) и задачи исследования на язык математики и для обратного перевода результатов на язык географии. При использовании ЭВМ необходим также набор правил дли выражения задачи на «машинном языке» (код команд ЭВМ), т. е, программирование алгоритма (последовательность математич. операций) задачи.

В экономич. географии, в отличие от многих гуманитарных наук, в к-рых М. м. ныне находят успешное применение (филология, лингвистика, история и др.), методы; напр., количеств, критерии для классификации, для типологии, характеристик, для выявления структурных соотношений и т. д. Поэтому применение М. м. в экономич. географии не связано с необходимостью коренной ломки. Давние и устойчивые традиции применения количеств, методов, использования и обработки статистич. материалов и т. д. облегчают орга-нич. сочетание в экономико-географич. исследованиях новых М. м. с классич. методами.

В то же время внедрение современных М. м. и ЭВМ в экономия, географию, несомненно, представляет собой качественно новый этап её развития, связанный с общими тенденциями развития современной науки и с новыми конструктивными задачами самой экономич. географии.

Современные М. м. в э. г. существенно отличаются от традиционных количеств, методов и по их роли в процессе эк.-теогр. исследования, л по научному уровню. При применении традиционных количеств, методов экономич. геогр. роль и влияние различных факторов оценивались гл. обр. качественно, а соотношения показателей оставались обычно лишь цифровой иллюстрацией. Изучение причинных связей редко доводилось до установления строгих корреляционных или функциональных зависимостей, что необходимо для количеств, прогноза и для конструктивного практнч. применения результатов исследования.

Из всего многообразия статистич. приёмов обработки цифровых данных в экономич. географии использовались преимущественно процентные соотношения и арифметич. средняя; даже др. типы средних (гармоническая, геометрическая, квадратичная, медиана, мода) почти не применялись. Счётная техника экономи-ко-географа ограничивалась обычно конторскими счётами, линейкой и арифмометром.

Напротив, современные М. м. в экономич. географии включают использование различных ветвей высшей математики (от «классических» до ультрасовременных). Счётно-решающая техника экономико-геогра-фа ныне включает цифровые и аналоговые УВИТ. Применение М. м. в экономич. географии иераз-рыипо связано с повышением её теоретич. уровня, с углублением, уточнением и известной формализацией всех её категорий и понятий, введением строгой и последовательной терминологии и системы обозначений, удовлетворяющих требованиям семиотики. Ранние опыты применения М. м., в частности, связаны с т. наз. центрографией7 предложенной Д. И. Менделеевым и развитой в 20-х годах Е. Е. Святловским и его школой в СССР. При ошибочности некоторых положений центрографии практические её методы нашли применение в географии (в США и других странах) для решения частных задач. D последние десятилетия М. м. находят всё возрастающее признание и применение в экономия, географии в СССР и за рубежом. Достигнуты существенные успехи в исследовании с помощью М. м. многих физико-гсографич. и экономико-географич. явлений и процессов и для решения практич. задач в деле использования природных ресурсов, размещения х-ва и поселений, районной и городской планировки.

Определённую пользу даёт перенесение и экопомич. географию М. м., оправдавших себя в теоретич. экономии и особенно в конкретных экономиках (напр., методы оптимизации размещения с помощью матема-тич. программирования). Но для исследования коренных проблем экономич. географии, теоретических и прикладных вопросов территориальной структуры и территориальной организации хозяйства (в частности — территориально-хозяйственных комплексов разных порядков) эти методы явно недостаточны. Экономич. географин ищет и находит собственные М. м., адэкватные её географич. специфике.

М. м. в определённой мере абстрагированы от при роды изучаемых явлений: один и тот же метод часто пригоден для исследования самых разнородных проблем. Вместе с тем формально совершенно различный М. м, подчас применимы для исследований тесно связанных между собой и родственных явлений или для решения сходных прикладных задач.

Важнейшие области применения М. м. в экономич. географии и типы задач, решаемых с их помощью.

1. Законы вариации величин, отражающих размещение населения, хозяйства, ресурсов. Сюда относится, в частности, изучение географпч. различий в густоте и плотности явлений (т. е. дазнметрнческцх показателей населения, дорожной сети, продукции и т. п.).

Примером служат закономерности внутригородского рассоления. Для городов с радиальной одпоцснтровой планировкой и одинаковым убыванием густоты населения по всем направлениям можно в любой точке вычислить плотность населения по формуле (Колнна Кларка.Англия)

, где S— плотность населения в рассматриваемой точке города; r_i,j — расстояние от центра; а — наибольшая плотность в центре города; бэта — темп убывания плотности населения от центра к периферии — постоянная для каждого города; е — основание натуральных логарифмов (е » 2,718...). Формула Кларка была усовершенствована Ю.В. Медведковьтм (СССР) и распространена па города, в к-рых плотность населении убывает от центра к периферии неодинаково по разным направлениям; в этом случае параметр бэта находится в функциональной зависимости от азимута каждого радиального направления Математпч. теорию географии расселения Б. Л. Гуревич и Ю. Г. Саушкпн развили и дополнили исследованием разных типов городов с радиальной структурой.

Эти формулы могут быть обобщены и распространены на города с линейным расположением (вдоль морского берега, реки, жел. дороги или автострады), либо е многоцентровой радиальной или смешанной планировкой и т. д.; обобщённая формула выводится путём наложения друг на друга простых закономерностей, выражающих падение плотности населения с удалением от разных центров (или линий) наибольшей плотности. Математически это выражается суммированием соответствующих показательных функций

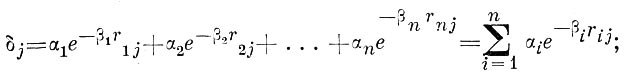
здесь о_j — плотность населения в j-той точке, r (i,j) — расстояние данной j-той точки от i-того центра (или линии) сгущения населения; п— количество таких центров пли линий; альфа — «идеальная» (абстрагированная от влияния других центров) плотность в этом центре сгущения или на линии сгущения, бэта _i — темп падения плотности при удалении от этого центра (линии). При исследовании дозиметрических величин выявляется, что влияние факторов, вызывающих географич. различия в густоте явления (дазигеничные факторы), убывает с расстоянием. Иногда ато убывание выражается количественно не показательной, а степенной функцией (например, обратно пропорционально квадрату расстояния).

2. Локальные или порайонные параметры структуры (состава населения, отраслевого состава пром-сти или с. хоз-ва, использования земель и т, д.).

Для характеристики географич. совокупностей служит коэффициент равномерности структуры, исчисляемыи по формуле (V . Мсресте, СССР)

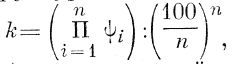
где n — число членов совокупности (напр., число районов в стране); П—знак произведения. В качестве сомножителей

берут удельные веса всех членов совокупности (районов). Коэффициент k может принимать любые значения между 0 и 1. Чем k больше, тем равномернее структура совокупности. Когда i показывают долю районов в площади страны,' k достигает максимального значения (единицы), если все районы одинаковы по площади. У. Мересте применял этот коэффициент для характеристики адм.-территориального деления Эст. ССР, структуры с.-х. земель и размещения промышленности Эстонии.

3. Локальные и порайонные параметры географической концентрации или дисперсии {т. е. распыления). Простейшие из них — это удельный вес или порядковый помер каждого пункта (района) по какому-то абсолютному показателю. Более совершенные и сложные показатели исчисляются по формулам:

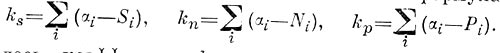
Здесь коэффициент k_s сопоставляет концентрацию изучаемой отрасли с распределением территории, k_n - с размещением населения, k_p — с размещением всей пром-сти в целом; i — номер района или центра; a j — доля i-того района (центра) в данной отрасли пром-сти страны (по продукции, занятости или фондам); Р _i — его доля в общем пром. произ-вс; N_i — доля в населении страны; S_i — доля района в площади территории. Могут применяться и комбинированные коэффициенты, например (k_nk_p)^1/2 (для районов и центров) (k_s k_n k_p)_1/3 (для районов); они представляют собой геометрическую среднюю двух или трёх простых коэффициентов концентрации. Эти показатели применяются в исследованиях С. Флоренса и У. Айсарда (США), И. М. Масргойза (СССР) и др.

4. Локальные или порайонные показатели динамики, напр, темпы роста населения, продукции пром-сти и т. п. в разных районах страны. Показатели темпов роста в экономии, географии (как и в экономии, науках вообще) выражаются математически логарифмической производной рассматриваемого показателя (х) по времени (t): у=dx/dt

на практике среднегодовые темпы роста показателя (х) за период (t лет) определяют обычно по формуле:

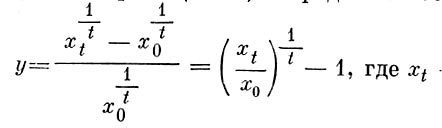
х_t - величина показателя в конце периода, а х₀ — в начале периода.

5. Локальные или порайонные параметры интенсивности и потенциала. Некоторые из них позволяют представить экономико-географич. пространство в виде потенциального поля, где понятие потенциала в каждом пункте соответствует суммарному влиянию в нем определённого фактора, распространённого по всей территории. Так, демографический потенциал исчисляется

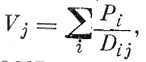
по формуле (Стюарт, США) , где P_i — людность i-того пункта; D_i,j — расстояние от него до рассматриваемого пункта (i-того); V_j— потенциал в i-том пункте. Напр., чтобы исчислить демографический потенциал в Новосибирске, число жителей каждого пункта страны (или малого р-на) нужно разделить на расстояние от этого пункта до Новосибирска и полученные частные сложить.

6. Структура сетей и географических систем дискретных пунктов (центров). Таковы системы поселений, пунктов, пром. центров, трансп. узлов, торговых и др. пр-тий.

Установлен ряд закономерностей, характеризующих густоту и взаимное расположение населённых пунктов. Используется так наз. критерий ближайшего соседства R=zn/zsf. В правой части формулы числитель обозначает среднее арифметическое всех фактич. расстояний между соседними поселениями в р-не; знаменатель — вероятная дальность ближайшего соседства при случайном размещении поселений: z _st = 50 * Г ^-1/2 , где Г — густота сети поселения в р-не (число поселений на 105 км2 площади). Значения R колеблются в узких границах, от 0 до 2,15, Близкое к 0 значение Л соответствует предельно агломерированной (сгущённой вблизи одной точки) сети поселений; .R = 1 — размещению поселений под влиянием множества факторов, среди к-рых нет нп одного ведущего. Верхний предел характерен для сети поселений, построенной строго регулярно (оптимальной по теории В. Кристал-лера). Значения R для групп поселений, классифицированных по градациям людности, образуют «семейство» параметров R1, R2,....Rn. Как показал К). Медведков, это ценный инструмент для сравнительного гео-графпч. анализа структуры всей сети населённых пунктов разных р-нов.

Средняя взаимоудалённость поселений какой-либо территории во многих случаях влияет на характер территориалыю-экономич. связей всех типов и величину средней дальности перевозок грузов и пассажиров и т. д. Отсюда можно узнать интенсивность связей и мощность обусловленных ими потоков. Среднее расстояние между пунктами страны (обозначается b>r)

задано формулой

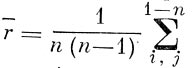
расстояние между i-тым и j-тьм пунктами, n — общее число пунктов. Для расчётных целей пользоваться такой формулой было бы чрезвычайно громоздко и сложно. Например, одних ж.-д. станций в СССР имеется более 10 тыс. Чтобы учесть их, нужно взять1/2(10000-9999), т. е. почти 50 миллионов отдельных расстояний между разными парами станций, сложить их между собой п разделить на число сочетаний. М. м. дают возможность представить приблизительную величину г как функцию нескольких важнейших параметров, характеризующих площадь территории, её форму и размещение сети пунктов. При этом расстояния можно измерять по кратчайшей трассе (ортодромии) или по путям сообщения. В последнем случае на величину r влияет также конфигурация трансп. сети. Величина г тесно связана с площадью территории (S) и ее наибольшим поперечником(D), так что r—Arj/5 и r—f.D. Коэффициенты k и % (каппа) варьируют в довольно узких границах (гл. обр. в зависимости от формы территории и от типа и конфигурации сети путей сообщения).

7. Структура линейных сетей (путей сообщения, линии связи п электропередач, водоснабжения и др.). Структура разнородных по своей природе линейных сетей характеризуется значительным формальным подобием, что позволяет применять для их анализа сходные М. м. {в первую очередь топологические — теорию графов и др.).

8. Территориально -экономические связи п взаимодействия: грузопотоки, товаропотоки в стоимостном измерении; продуктонотоки в натуральных измерителях; миграции населения, пассажиропотоки, финансово-кредитные связи, потоки информации и т. д. Они могут быть международными, межрайонными (в пределах страны) или межпунктовыми.

Разработка математической теории транспортно-экономических и других территориально-экономических связей даёт возможность по-новому подойти к исследованию вопросов территорпалыю-географич, разделения труда. Найдены формулы (Л. И. Василевский), характеризующие интенсивность террито-риально-географич. разделения труда в пределах изучаемой территории, пригодные для сопоставления стран и районов разных размеров.

9. Размещение предприятий, комплексов и отраслей хозяйства. М. м. позволяют количественно оценить влияние разных условий и факторов на размещение производств, роль сочетания разных факторов и условий

(в т.ч. явлений агломерации и интерференции отраслей в произв. комплексе). Разработан ряд М. м. исследования, а также показателей размещения отраслей пром-сти по р-нам и центрам (работы С. Флоренса, У. Айсарда, Р. Хартсфорда, Ч. Колби, X. Мак-Карти, Э. Гувера — в США; П. Н. Степанова, А. Е. Пробста, Н. В. Алисова, В. М. Гохмана, Ю. К. Козлова, И. М. Маергойза и др. — в СССР; А. Куклиньского— с Польше и т. д.). Разрабатываются также М. м. и показатели для изучения размещения сил. х-ва (А. Г. Аганбегян, В. С. Мпхеева, A. TI. Ракитников, Е. М. Четыркин и др.—в СССР). Разработаны методы экономич. (интегральной и синтезирующей) оценки земель для разных природных зон и способов ведения хозяйства (Б. Л. Гуревичи И. М. Ланда).

Заложены основы классификации типов размещения пром-сти и сел. х-ва, исходя из количественных критериев. Есть первые опыты по выделению с помощью М. м. отраслевых, а также комплексных общсэконо-мич. р-нов (Ю. Г. Саушкпн и др. —в СССР, Л. Зоб-лор — в США).

10. Планирование размещения производительных сил. До наст, времени М. м. в планировании используются гл. обр. для решения краткосрочных задач или задач узкого характера (размещение отдельных предприятий, распределение заданного объёма продукции между заранее локализованными предприятиями и т. п.). Для применения М. м. к более широким задачам перспективного планирования необходимо:

а} дальнейшее изучение экономико-географич. закономерностей, с тем чтобы представить пх в виде математпч. функций; б) развитие математич. аппарата оптимального программирования,

11. Балансы меж отраслевых н межрайонных связей. Методы анализа межотраслевых балансов п балансов затрат-выпуска и их оптимизации с применением линейного программирования и др. М. м. хорошо разработаны экономистами (В. В. Леонтьев, X. Ченери и П. Кларк в США; 0. Ланге — в Польше; В. С. Немчинов, В. В. Коссов и др.— в СССР). Есть первые попытки сочетания межотраслевого баланса с межрайонным в одной математич. модели. Ещё не преодолены полностью принципиальные трудности в задаче построения оптимального баланса связен на перспективу с учётом взаимодействия отраслей и обратного влияния плановых решений по отдельным отраслям и районам на условия оптимизации решении по другим отраслям п районам.

12. Математические модели экономики страны {или раиона) в целом. Ведётся, в частности, разработка системы параметров для количественной характеристики абстрактного хозяйственного пространства, т. е. многомерной математнч, модели, отображающей структуру, динамику и размещение народного хоз-ва в целом. В этой области выделяются работы В. С. Немчинова, А. Г. Аганбегяпа, С. М. Вишнева н других сов. экономистов математич. направления.

13. Операции исследовательского процесса в экономич. географии: отбор и генерализация; переход к карте от текстовых, цифровых и графич. материалов, а также переход от карты к математизированной картосхеме (или картопомограмме ) и далее — к выраженным аналитически (с помощью математич. формул) закономерностям географич. размещения (работы У. Бунге в США и ряда советских экономико-географов); работа Р. Даманьского по М. м, типологических исследований в экономич. географии в Польше.

Создание логико-математпч. теории отбора и генерализации в экономич. географии ещё не завершено. Предлагают применять для этих операций наряду,

с классич. методами также методы «эвристического программирования» (М. м. для решения задач с неполной информацией) и ЭВМ (не только цифровые, по п аналоговые).

Основные типы М. м. в экономической географин.

Применяемые в теоретпч. и прикладной экон. географии М. м. можно отнести к нескольким типам:

1) Статистико-математические методы. Они позволяют выявлять наличие взаимосвязи или причинной зависимости между явлениями путём установления корреляции статистич. рядов. Параллельность изменения разных показателей за ряд лет (корреляция временных рядов) выявляет либо прямую причинную зависимость между изучаемыми явлениями, либо наличие общих факторов, обусловливающих сходную динамику явлений.

В экономич. географии особенно важно установление корреляции пространственных рядов, в к-рых сопоставляются показатели по разным странам, районам или пунктам.

Так, сравнение душевого национального дохода н подвижности населения (пасс.-км на 1 чел. в год) для разных ка-питалистич. и развивающихся стран показывает высокую степень корролящш обоих статпстич. рядов. Это отражает тесную зависимость между транспортной подвижностью населения и уровнем экономия, развития. Сравнение аналогичных рядов по районам одной страны {например, по штатам США} подтверждает эту закономерность (работы Б. Ы. Пя-рахонского, Л. II. Василевского н др.). Корреляция временных рядов, характеризующих динамику тех же показателен (подвижности населения п душевого дохода), позволила разработать методику прогноза пассажирооборота на перспективу (Б. М. Парахонский, Т. А. Пахман, О. Д. Кибальчич и др.).

К числу статистико-математич. методов относится и многофакторный анализ. Сущность этого метода состоит в замене большого числа показателей, варьирующих по странам или р-нам, меньшим набором комплексных параметров, называемых иногда «аспектами». Каждый комплексный параметр включает группу исходных показателей, выделенную по признаку общности пли сходства порайонных изменений. Напр., удалось свести 43 показателя экономич. развития, варьирующих по 95 странам, к 4 комплексным «аспектам» (Б. Берри). Мпогофакторный анализ позволяет найти фундаментальные факторы экономико-гео-графнч. вариации, т. е. различия изучаемых явлений в разных р-нах и пунктах. Этот метод можно определить как математически обоснованную конденсацию характеристик стран или районов, облегчающую выявление закономерностей и причинных связей (работы амер. географов А. Робинсона, Б. Берри и др., в СССР — В. М. Жуковской).

2) Методы анализа функциональных эмпирических зависимостей. Этими методами соотношения фактич. данных представляются в виде математич. функции, что позволяет глубоко исследовать колич. взаимосвязи явлений и процессов. Функции могут быть заданы аналитически (формулой) или графически. Пример результатов, полученных этим методом,— формула Зипфа (см. ниже).

3) Моделирование экономико-географич. явлений и процессов с помощью категорий и математич. аппарата физики и др. точных наук. Примером является моделирование географич. различий в уровне цен или в уровне себестоимости пропз-ва потенциальным полем, применяемым в математич. экономике. Стюарт ввёл понятие демографич. потенциала и наряду с ним понятия силы взаимодействия поселений и энергии их взаимодействия. Для изучения и прогноза пассажире- н грузопотоков (как и др. территориально-экономич. связей) также часто применяются гравитационные модели, т. е. эти связи и потоки исчисляют по формулам, сходным с формулами закона тяготения и законов Кулона. Применению гравитационных моделей и потенциального поля в экономпко-теографич. исследованиях посвящена, напр., работа 3. Хойницкого (Польша). Все эти методы позволяют привлечь для исследования географич. явлении богатый матоматич. аппарат физики; однако сходство между действительностью и моделью ограничено определёнными рамками; за их пределами аналогия становится неполной и может привести к неправильным выводам (напр., в центрографии).

Перспективное значение имеют «термодинамические» (вероятностные) модели экономико-географич. комплексов различного характера (напр., транспортных систем) с переносом в экономпч. географию из физики понятия энтропии и из биологии—противоположного ему понятия (нег-энтропия, спптроппя или эктроппя). Сннтро-пия равна логарифму вероятности состояния системы, взятому со знаком «минус» и является мерой организованности системы и объёма заложенной в ней информации. Рост энтропии свидетельствует о деградации системы, о потере информации; рост спнтроппп — о повышении организованности системы, качественного уровня её функционирования, о приобретении дополнительной информации (сведений, опыта работы). Исследования в этом направлении тесно связаны с теорией информации (и вообще с кибернетикой) и в особенности с развивающейся в наст, время новой наукой — общей теорией динамических систем.

4) Методы нахождения инвариантов, принципов сохранения, монотонных последовательностей и т.д. Примером служат введённые автором два транспорт-но-географич. параметра — средний радиус трапс-портно-экономнч. связей и географич. дальность перевозок (т. е. среднее расстояние между пунктами производства п пунктами потребления, в расчёте на единицу стоимости пли па 1 т продукции). Показатели косвенно характеризуют уровень географич. разделения труда, независимо от сетки и границ экономнч. р-нов. Интенсивность географпч. разделения труда выражается величиной

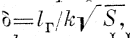
, где S — площадь территории грузообмена, k — коэффициент, зависящий от конфигурации территории, l_r — географич. дальность перевозок, исчисляемая в двух вариантах:

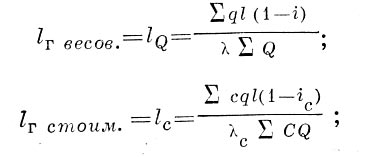
здесь q — вес груза, с — стоимость 1 т груза, t — расстояние перевозки, Q — вес продукции, С — стоимость 1 m продукции, (i и i_с— доля нерациональных перевозок в общем грузообороте (в т-км или в рубль-км); и — среднее удлинение маршрутов Перевозки по сравнению с ортодромией (на 1 т или на 1 руб. стоимости перевозимого груза).

5) Представление экономико-географических явлений в форме матричных моделей. Для математического моделирования структурных соотношений п связей в экономич. географии (как н в отраслевых экономпч. науках) широко применяются упорядоченные системы величин — векторы (система величин, расположенная в определённой последовательности) и матрицы (система величин, расположенных в форме прямоугольной таблицы). Типичным примером матриц, применяемых в экономич. географии в качестве мате-матнч. моделей, являются ||P|| — матрица размещения (производства, потребления или ресурсов) и ||Q|| — матрица территориально-эк он омжч. связей.

Прямоугольная матрица ||Р|| моделирует размещение разных видов продукции в п районах страны. Буквами — от a до z — обозначены виды продукции; цифровые индексы у букв означают №№ районов; например, с₅ означает объём производства третьего вида продукции в 5-м районе и т. д. Каждая строка таблицы — вектор, характеризующий объём и состав продукции всех отраслей производства в одном из районов; каждый столбец таблицы — также вектор, характеризующий объём п размещение производства одпого из видов продукции по всем районам. Число столбцов, вообще говоря, не равно числу строк.

Квадратная матрица || Q || моделирует террнториально-зкономич. связи (по одному виду продукции или по всем видам продукции, вместе взятым) между районами страны. Поэтому число строк в этой матрице равно числу столбцов. Элемент этой матрицы (например, 35 и q₅₃) характеризует двусторонние транслортно-экономические связи между районами. Так называемый «след» матрицы — сумма элементов, лежащих на главной диагонали,— показывает общпй объём производства во всех районах для местных нужд. Сумма остальных элементов матрицы равна общему объёму продукции, перевозимой в межрайонных сообщениях. Каждая строка этой матрицы {q_i1 q_i2...q_in} ~ вектор, характеризующий размер производства в одном районе n её состав по местам назначения.

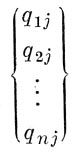
Каждый столбец этой матрицы вектор, характеризующий размеры потребления в одном из районов и её состав по местам производства. Приведённые примеры, разумеется, не исчерпывают всех типов матриц, применяемых в экономпко-гео-графпч. исследованиях. Матричная модель отображает в компактной, обозримой и доступной для математич. исследования форме основные структурные (топологические) п количественные (метрические) черты сложного комплекса явлений (в приведённых выше двух примерах — размещения производства п системы межрайонных связей). На матричных моделях решаются и задачи по оптимизации размещения или террнторпально-экономич. связей.

6)Экономико-аналитические и географо-аналитическпе методы. Здесь в формулу математич. функций облекаются закономерности и взаимосвязи, уже осознанные качественно; при этом колич. закономерности выводятся дедуктивно, исходя из знания природы явления и логич. анализа механизма действия причинных связей, и лишь проверяются на отатистнч. материалах.

Например, удалось выразить уравнением закономерную связь между людностью городов страны. Правило Зипфа представлено формулой Р_j = Р₁*j^-a, где j — порядковый номер города при расположении их по убывающей людности; Р_j - людность такого города; Р₁ — людность крупнейшего города той же системы. Проверка формулы Зипфа для ряда стран показала высокую степень совпадения теории с фактами. Показатель степени в формуле Зипфа — параметр о. — исторически меняется (для США он уменьшился С 0,92 в 1950 ДО 0,8 в 1960). Общая сеть городов США и др. крупных стран включает региональные сети, для к-рых формула К. Г. Зппфа справедлива, но с иными параметрами (Ю. Мед-ведков). Формула Зппфа может быть выведена и дедуктивно из основных положений «теории центральных мест» Кристаллера, а также из общих соображений о системах объектов, взаимозависимых в своём росте (работы М.Бекмана, Берри, У. Гаррисона и др.). Правило Зппфа связано с закономерностями географии густоты населения (исследования Боуга, Томаса, Стюарта, У. Уорнца и др.).

Связь между основными девятью параметрами географин расселения выражается след, системой уравнений (В. Г. Давидовича):

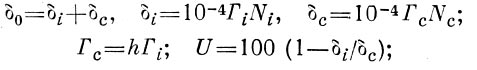
здесь s₀ — общая плотность населения, s₁ и s₂ - плотность городского и сельского населения соответственно, Г_i и Г_с— густота сети городов и сельских поселений; N_i и N_с — средняя людность городов и сельских поселений; U — % городского населения; h — число сельских поселений, приходящихся па 1 город. Только 4 из этих 9 параметров можно рассматривать как независимые переменные. Нерешённой задачей остаётся синтез математпко-географич. теорий расселения (размещения поселений, соотношения их людности и т. д.) с типологией и экономпч. географией населённых пунктов. Для этого необходимо БВРСТИ в формулы наряду с демография, параметрами ещё и параметры, характеризующие роль населённых пунктов и их экономику.

Важным примером применения аналптпч. метода является теория т. н. производственных функции, выражающих зависимость объёма продукции от затрат и условий производства. Уравнение производственной функции в матричной форме имеет вид |Р| = Q |R|, причём 9. — оператор, символизирующий алгоритм перехода от матрицы ||P|| к ||R||;

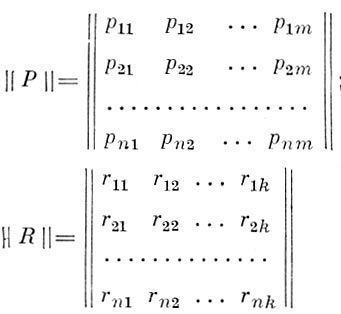
Здесь ||Р|| — это матрица продукции; ||R|| — это матрица затрат. Отдельные элементы обеих матриц выражают: Р_i,j — выпуск j-того вила продукции, а г.- — затрату ресурсов j-того рода в i-том пункте или районе.В такой форме производственная функция отражает одновременно структуру и размещение продукции в связи со структурой и размещением затрат, т. е. носит ярко выраженный экономико-геогра-фичссннй характер. От производственной функции в общей операторной форме необходимо отличать скалярные ур-ния

вида

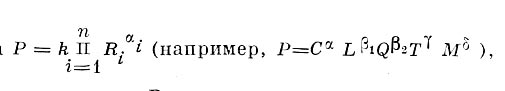
где Р и все сомножители R_i — вещественные положительные числа: P — объём продукции, С — сумма материальных затрат, L — затрата живого труда, Q — уровень квалификации работников, Т — уровень техники; показатели степени aльфа, бэта1, бэта2,гамма и сигма и определяются эмпирически для какой-либо отрасли или всего производства в стране (р-не) в целом. Сомножителю Т*гамма часто придают форму е_{гамма*Т} (где t — время, гамма — темп тех-нич. прогресса, а е — основание натуральных логарифмов). Проверка этих формул па статпстич. материале ряда стран (Кобб, Дуглас и др. в США; С. М. Вишнев в СССР) показала, что параметры a, в, г,... неодинаковы для разных стран, по относительно устойчивы з динамике для каждой из них. Предлагалась и более общая форма скалярного ур-ния производственной функции — произведение степенных рядов (как известно, обширный класс функций выражается сходящимися бесконечными степенными рядами, к-рые приближённо можно заменить конечными)

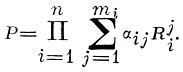
Здесь R j — разные факторы и условия производства — затраты материальных ресурсов, сгруппированных по важнейшим видам; затраты живого труда разной сложности; измерители тсхнич. оснащённости; объём исследований, конструкторских работ и т. д. Коэффициенты и показатели степени уравнений произв. функции в скалярной форме для стран н районов, по общему объёму пронз-ва и по отдельным отраслям, можно определять методом наименьших квадратов пз ста-тистич. данных за ряд лет. В последующем этот метод может служить инструментом для решения задач перспективного планирования, с учётом географкч. различий в производительности труда н всех меняющихся факторов и условий.

7) Методы математического (оптимального) программирования. Наиболее разработанный из методов этой группы— линейное программирование — в экономич. географии применяется гл. обр. для решения прикладных задач по оптимизации размещении производства или транс-портио-экономич. связей. Напр., с помощью этого метода находится распределение заданного объёма производства между районами, при к-ром сумма затрат была бы наименьшей (задача на минимизацию затрат). Обязательно соблюдение ряда дополнительных ограничений (напр., объём производства в каждом р-не не может превысить определённый максимум и не должен быть ниже минимума, необходимого для удовлетворения местных нужд). Типичный образец линейного программирования — решение т. н. трансп. задачи, т. е. прикрепление поставщиков (пунктов производства или отправления грузов) к потребителям с тем, чтобы общий пробег грузов в ni-км или общий объём затрат на перевозку был минимальным, а потоки грузов не превышали пропускной способности каждой дороги. В задачах линейного программирования необходимо, чтобы подлежащий оптимизации показатель был выражен уравнениями первой степени от независимых переменных; все ограничения также должны иметь вид линейных неравенств или равенств.

Методы нелинейного программирования — выпуклого (квадратичного) и высших степеней, целочисленного и динамического — ещё слабо разработаны (лад разработкой проблем квадратичного программирования работает Рагнар Фриш в Норвегии). При решении задач нелинейного программирования часто применяются итеративные методы — постепенное приближение к оптимальному решению путём многократного повторения упрощённых расчётов, с использованием в каждом последующем «туре», в качестве исходных данных,— результатов, полученных в предыдущем «туре» решения.

8} Применение теории графов. Граф, выражаясь описательно, это совокупность точек (вершин), соединённых линиями (ненаправленные линии называют рёбрами, направленные — дугами). Расположению вершин, длине и форме рёбер или дуг графа не придаётся значения: существенно лишь, какие вершины между собой соединены. Граф можно отождествлять с системой точечных и линейных объектов на территории и с др. системами взаимосвязанных объектов или даже логич. категорий л понятий. Методами теории графов исследуют разнообразные картосхемы, а также всевозможные логич. схемы—классификации, соподчинения, развития, и решают ряд задач на оптимизацию. Теория графов очень полезна при исследовании структуры транспортных сетей (К. Канский в США, Л. Василевский и др. в CCCР), сетей связи, потоков и т. п. Особенно плодотворно моделирование эконом.-географич. пространства с помощью размеченных графов, в к-рых вершинам и дугам, кроме взаимного положения, приписывается колич. или качественное значение.

9) Картометрические методы. На экономич. и демографич. картах многих типов (фоновых картограммах, картах с изоквантами, точечных — и вообще картах статистич. поверхностей) можно устанавливать форму и степень связей между показателями, а иногда и выражать их в аналитич, форме (анализу корреляционных связей по географич. картам посвящена работа В. А. Червякова под руководством К. А. Салищева).

Возможности картометрич. методов особенно велики для новых типов «математизированных» картоно-мограмм. В частности, у анаморфированных карт в разработанных автором варнавалентных проекциях отображаемый экономим, показатель введён в самую картография, проекцию; напр., на эквидемической карте участки территории изображены в размере, пропорциональном численности населения. Нанесённые на такую карту показатели воспринимаются визуально как отнесённые к размерам населения, а не к территории. Переход от эквивалентной к ва-риавалентной псевдоцилиндрич. проекции выполняется по формулам (Л. Василевского):

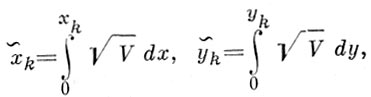
где x_k, y_k — декартовы координаты географич. пункта

«К» в плоскости эквивалентной карты, a xl{. yh — в плоскости анаморфированной карты. Переход к азимутальной вариавалентной проекции выполняется

по формулам:

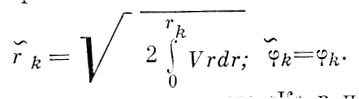
Здесь r_k, f_k — полярные координаты пункта «К» в плоскости

эквивалентной карты, r_k, ф _k — в плоскости анаморфированной карты. В обоих случаях V — варьирующий показатель — функция от координат х и у (или от r и ); для эквидемпческон проекции это—отношение плотности населения в ближайшей окрестности точки к средней плотности населения всей территории. Анаморфированные карты (без математич. обоснования, составляемые путём грубой схематизации географич. очертаний) нашли ряд применений в США и др. странах.

Центрография также может быть отнесена к группе картометрич. методов; её сущность сводится к усреднению параметров географич, размещения изучаемого явления. Например, координаты «центра населения» страны исчисляются как взвешенные средние соответствующих координат всех населённых пунктов. Такие центры имеют все достоинства н недостатки обычных статистических средних, они, естественно, не характеризуют всей сложной картины размещения. Картометрич. метод построения географической медианы, предложенный чешек, учёным Я. Корчаком, сводится к нанесению линий, делящих территорию района на две части, в каждой из которых расположена половина рассматриваемой статистич. совокупности

(напр., населения). Эти линии рекомендуется проводить, где это возможно, через географич. ориентиры (водоразделы, орографич. границы и т. д.). Географич. медиана дополняет статистич. карты или картограммы, наглядно изображая географич. расположение показателей, интенсивность которых выражена другими средствами (тон закраски, густота штриховки п т. п.). Применение совр. математич. методов в экономии, географии находится в начальной стадии развития. Естественно, поэтому, что многие вопросы, связанные с внедрением М. м., нуждаются в детальном изучении. В то же время несомненно, что широкое освоение М. м. будет способствовать углублению зкономико-географцч. исследований, в соответствии с требованиями современного уровня развития науки и всё более возрастающих запросов практики.

Лит.: Лганбсгин А. Г., Ыихеева В. С., Об определении экономически эффективного размещения сельскохозяйственного производства по природно-хозяйственным районам страны, в сб.: оптимальное планирование, Экон. математпч. серия, вып. П1, Новосибирск, 1962; Аплен Р. Д., Математическая экономии, пер с англ., М 1963; Берк К., Теория графов и ее применения, пер. с франц., М., 1962; Боярский А. Я., Математика для экономистов, 2 изд., М., 196Г, Василевский Л, И., Соотношение между грузооборотом п объемом производства в капиталистических странах, в сб.: Зарубежный транспорт, Ы., I960; его же, Транспортная система США: сравнительный экономический анализ, в сб.: Соревнование двух систем. Проблещи экономической науки, М., 1963; Геил Д., Теория линейных экономических моделей, пер. с англ., М., 19(53; География городов. Сб. ст., под ред. Г. Ы. Найсра и К. Ф. Кона, пер. с англ., Ы.. 1965; Количественные методы исследования в экономической географии. (Сб. окладов на семинаре), под ред. И. М. Ма-ергойза, М., 1964; Коссов Н. Е., Экономико-математическая модель территориального планирования, в кн.; Математические методы и проблемы размещения производства, М., 1963; Ланге О., Введение в эконометрику, пер. с польск., М., 1964; Лёш А., Географическое размещение хозяйства, пер. с англ., М., 1959; Леонтьев В. [и др.], Исследования структуры американской экономики. Теоретический п эмпирический анализ по схеме затраты— выпуск, пер. с англ., М., 1958; Математические методы н проблемы размещения производства. [Сб. ст.], под ред. И. Я. Бирмана и Л. Е. Минца, М., 1963; Медведков Ю. В., Приложении математики к некоторым задачам экономической географии, в кн.: Географический сборник. Работы по теоретическим и спец. вопросам научно-технической информации, М., 1963, с. 4-7—64, его же, Приложения математики в экономической географии, 51., 1965; Михалевский Б. Н., Перспективные расчеты на основе простых динамических моделей, М., 1964; Немчинов В. С., Экономико-математические методы п модели, Ы., 1962; Нестеров Е. П-, Транспортные задачи линейного программирования, М., 1962; Планирование и экономико-математические методы. [Сб. ст. к 70-летню со дня рождения акад. В. С. Немчинова, М., 1964; Пробст А. Е., Размещение социалистической промышленности. (Теоретические очерки), М., 1962; Саушкин Ю. Г., Построение экономико-географических моделей районов для рационального размещения промышленности, в кн.: Труды конференции по вопросам размещения промышленности и развития городов, Ннльнюс. 1963; Флоренс С., Структура промышленности и управление предприятиями Британии и США, пер. с англ.. М , 1958; Xачатуров Т. С, Экономическая эффективность капитальных вложений, Н-, 196'i; Ченери X. Б и Кларк П, Г. Экономика межотраслевых связей, пер. с англ., М-, 1962; Эшби У. Р., Введение в кибернетику, пер. с англ., М.. 1959; Isard \V., Methods of regional analysis, L., 1960; Avоndо Bodino G.. Economic applications of the theory of graphs, N. У., 1962; Berry B. J. L. and Garrison W. L., A note on central place theory and the range of a good, «Economic Geography», 1958, v. 34, p. 304 — 11; Bunge W., Theoretical geography, Lund, 1962; DomaUsKi R., Pro-cedura typologiczna w hadaniach ekonomiczno-gcograficznycli, «Przeglad geograficzny», 1964, 36, ,№ 4, s. 627 — 60; Duncan O. D,, Cuzzort R. P., Beverly D-, Statistical geography, problems in analyzing areal data, Glen-epe (111.), 1961; Garrison W. L., Applicability of statistical inference to geographical research. «Geographical Review», 1956, v. 46, p. 427 — 29; его же. Spatial structure of the economy, «Annals of the Association of American Geographers», 1959—60, v. 49—50; pt 1—3; Garrison "W. L. [a. O.J, Studies of highway development and geographic change, Seattle, 1959; Gregory S., Statistical methods and the geographer, lL., 1963]; Isard I \V., Location and space-economy, N. Y., 1960; Кanskу К. J., Structure of transportation networks. Relationships between network geometry and regional сharacteristics, Chi., 1963; Koopraans Т. C. ta.o.J, Activity analysis of production and allocation, N. Y., 195t; К о г б a k J., Geograficky median, «Shornlk CcskoslovensJie spolefinostl zemepisne», 1У62, v. 67, J\i° 2; Lcfeber L., Allocation in space. Production, transport and industrial location, Amst., 1958; Merest e U., Koguraite struktuuri siin-teetitisest iscloomustamiscst inajandusgeograatilistes uuri-mustes, «Eesti Geogr. Seltsi aastaraamat I960 — 61», Tallinn, 1962; Thrower N. J. W-, Animated cartography, «Professional Geographer», [959, v. 11, Mi 6; Warntz W-, Transportation, social physics and the law of refraction, там же, 1957, v. 9, Л'а 4.

Л.Л. Василевский.

Источники:

1. Краткая географическая энциклопедия, Том 5/Гл.ред. Григорьев А.А. М.:Советсвкая энциклопедия - 1966, 544 с. с илл. и картами, 5 л. карт иилл., 1 л. карта-вкладка