Движение полюсов Земли

После того как был установлен факт изменяемости широт точек земной поверхности, начали искать причины этого явления. Так как географическая широта места есть угол между отвесной линией в данном месте и плоскостью земного экватора, то изменяться широта могла либо от изменения направления отвесной линии, либо от перемещения оси вращения Земли внутри самого земного сфероида. Однако направление отвесной линии изменялось лишь от возмущающего действия Луны и Солнца и то незначительно. Оставалось допустить второе - изменение положения оси вращения в теле Земли. Заметим, что такое предположение имело некоторое основание: высокоточные наблюдения, проводимые на различных обсерваториях земного шара и использованные для получения одних и тех же астрономических постоянных величин (с учетом широты места наблюдения), приводили к противоречивым результатам. Подобное расхождение наглядно выявилось при определении поправки к постоянной аберрации В. Струве пулковским астрономом М. Нюреном и астрономом Берлинской обсерватории Ф. Кюстнером.

Если широта места наблюдения действительно изменяется от изменения положения оси вращения в теле Земли, то величина изменения широты в местах, расположенных на двух различных меридианах, отстоящих по долготе на 180°, должна быть одинакова, но с разными знаками: на какую величину в данный момент широта увеличится в одном месте, на такую величину она уменьшится на противоположном меридиане Земли.

Для проверки этого положения в 1890 г. в Гонолулу на Сандвичевых (ныне Гавайских) островах в Тихом океане была построена специальная обсерватория (широтная станция), отстоящая от Берлина по долготе на 180°.

Одновременные наблюдения в двух местах, в Берлине и Гонолулу, должны были или подтвердить гипотезу о смещении оси вращения в теле Земли, или опровергнуть ее. Оказалось, что кривая изменения широты Гонолулу является зеркальным отражением кривой изменения широты Берлина. Таким образом, было доказано, что изменение широты места на земной поверхности происходит от смещения оси вращения Земли в теле самой планеты. Но если ось вращения смещается, то точка пересечения этой оси с поверхностью Земли, иначе говоря, полюс Земли, смещается по ее поверхности, описывая некоторую кривую.

Исследуя это явление, Чандлер в конце прошлого века (1892) пришел к заключению, что наблюденные изменения широт изображаются кривой - результирующей двух периодических кривых, налагающихся одна на другую. Первая из них имеет период 430,7 суток и полуамплитуду около 0",12; вторая кривая - почти годичный период (364,9 суток) с полуамплитудой, лежащей между 0",04 и 0",20. Результаты Чандлера имели большое значение, так как они в основном удовлетворительно разъясняли суть вопроса и способствовали дальнейшему развитию исследований в этом направлении. Четырнадцатимесячный период (430,7 суток) движения полюса, или, как его называют, период свободной нутации, по праву получил название периода Чандлера.

В настоящее время, можно сказать, доказано, что центр Земли - ядро находится в жидком состоянии.

Из теории вращения Земли с жидким сжатым ядром вытекает, что при отсутствии внешних сил оболочка Земли, кроме чандлеровской нутации, может иметь еще одну нутацию с периодом около суток. Обработка больших рядов наблюдений (полученных более чем за 100 лет), проведенная за последние годы, подтвердила теоретические выводы и показала, что 430-суточным периодом не исчерпывается свободная нутация; имеется еще близсуточное колебание полюса, амплитуда которого изменяется со временем.

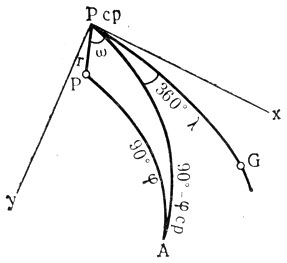
Рис. 18. Полюсы Земли. А - место наблюдения

В 1893 г. русский астроном С. К. Костинский вывел формулу, которая связывала изменение широт мест на земной поверхности с движением полюсов по поверхности Земли, т. е. давала возможность построить кривую движения географического полюса по поверхности Земли:

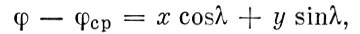
где φ_ср - средняя широта, о которой будет сказано ниже; φ - широта в данный момент, так называемая мгновенная широта; λ - западная долгота места наблюдения; х, у - координаты мгновенного полюса относительно его среднего положения, или, как говорят, среднего полюса.

Вывод формулы Костинского очень прост. Пусть (рис. 18) Р_ср - среднее положение полюса, Р - положение полюса в данный момент, т. е. положение мгновенного полюса, А - место, имеющее западную долготу λ, широта которого определяется. Если направить ось х по гринвичскому меридиану Р_срG, а ось у - к западу от него и обозначить расстояние между мгновенным Р и средним Р_ср полюсами r, а угол между направлениями х и r - ω, то, применяя к треугольнику AP_срP формулу для узкого сферического треугольника

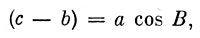
будем иметь

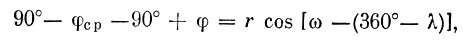
или

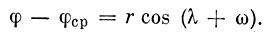
Если r cos ω = х и r sin ω = y, то получим формулу (10).

В формуле Костинского две неизвестные величины - х и у. Чтобы определить их, нужно иметь два уравнения, а для этого следует наблюдать за изменяемостью широт, по крайней мере, в двух пунктах. Наиболее выгодное решение задачи получается при разности долгот этих пунктов 90°.