8.6. Бюджет вещества, стационарное состояние и изменение формы ледника

Если известна продольная скорость V массы ледника, а также линии его тока, скорость поверхностной аккумуляции А, скорость таяния льда в базисном слое М и профиль толщины ледника Н, то скорость изменения толщины куполового ледника во времени над каждой точкой ложа 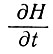можно рассчитать по уравнению

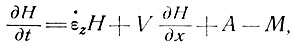
(44)

где 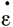_z - скорость вертикальной деформации, приближенно выражаемая суммой двух скоростей горизонтальной деформации (продольной и поперечной).

По формуле (44), выведенной для всей массы ледника, можно определить новую форму ледника, которая реализуется через заданный период времени, при условии, что параметры ледника за этот период существенно не изменятся. По мере изменения формы и размеров ледника будет формироваться новое распределение скорости движения, рассчитываемой по выражению для сглаженной скорости (38). Таким образом, можно определить историю и будущие состояния куполового ледника. Чем глубже экстраполяция во времени, тем менее точны ее результаты. Очевидно, что для долговременной экстраполяции необходимо знать величины долговременных колебаний скорости аккумуляции.

Очень специальным случаем, в котором 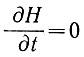по всей линии тока, является "стационарное состояние", когда форма и размер куполового ледника остаются постоянными во времени. Вообще, условие равновесия куполового ледника с толщиной Н, скоростью V на расстоянии r от его центра, где S_r - площадь, расположенная между линиями тока ледника на расстоянии s друг от друга и r от центра, а 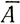_r - средняя скорость аккумуляции на этой площади, может быть записано в виде

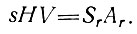
(45)

Использование уравнения (38) для определения значений скорости в величинах параметров течения, толщины льда и наклона поверхности дает возможность получить из уравнения (45) профиль поверхности, необходимый для получения условий равновесия куполового ледника, т. е.

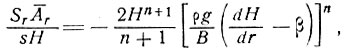
(46)

где 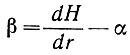- наклон поверхности. При условии, что все параметры известны как функции r, уравнение (46) можно численно проинтегрировать и получить установившийся профиль, соответствующий известным параметрам.

Кроме того, уравнения (45), (46) можно использовать, чтобы определить, какие величины перечисленных параметров, в частности А, V, В, потребовались бы для того, чтобы существующий профиль поверхности соответствовал состоянию равновесия.

Пути частиц льда при установившемся состоянии или траектории, прослеживающие пути льда, отложившегося на поверхности по мере его движения от поверхности, можно рассчитать по формуле

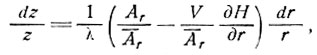
где z - глубина колонки льда на расстоянии r от центра, А_r - скорость аккумуляции на расстоянии r, 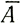_r - средняя скорость аккумуляции до расстояния r и

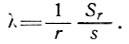
Для определения траекторий движения частиц льда в неустановившемся состоянии необходимо вместо фактической скорости аккумуляции А использовать скорость аккумуляции при состоянии равновесия:

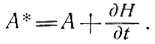
Кроме того, при расчетах, охватывающих длительные промежутки времени, необходимо изменить профили толщины льда и скорости в соответствии с уравнениями (45) и (38).