2.1. Тензоры напряжения и скорости деформации сдвига

Обозначим тензоры напряжения и скорости деформации сдвига следующим образом:

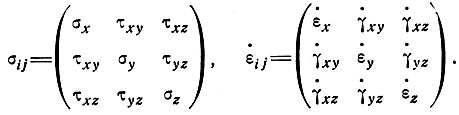
Главные напряжения и скорости деформации сдвига выразим через

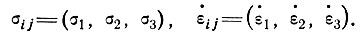
Условие несжимаемости тогда может быть записано в виде

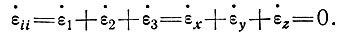
(1)

При этом гидростатическое давление р определяется по выражению

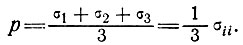
(2)

При скорости деформации чистого сдвига (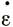_ii = 0) нас интересует девиатор напряжения σ'_ij, который не зависит от гидростатического давления и определяется через

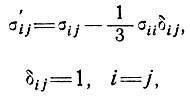
(3)

или

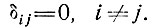
Глен [35] рассматривает обобщенные формы закона течения льда, включающие как вторые, так и третьи инварианты девиатора напряжения и тензоров скорости деформации. На настоящем этапе, однако, представляется, что экспериментальным данным можно дать удовлетворительное объяснение, используя более простой закон течения льда, включающий лишь вторые инварианты, которые обозначим как

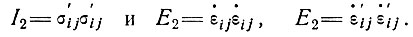
(4)

Най [86] постулировал закон течения льда типа

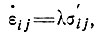
(5)

где λ - функция инвариантов I₂ и Е₂. При этом он выразил "эффективное напряжение сдвига" τ_э и "эффективные деформации сдвига" 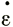_э через вторые инварианты (см. Ягер [46]):

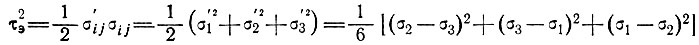
(6)

и

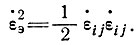
Вторые инварианты можно выразить и в величинах напряжения сдвига на октаэдрической сдвиговой плоскости, нормаль к которой имеет направляющие косинусы 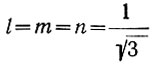относительно главных осей. Нормальное напряжение на этой плоскости равно гидростатическому давлению. Октаэдрическое напряжение сдвига и скорости деформации определяются выражениями:

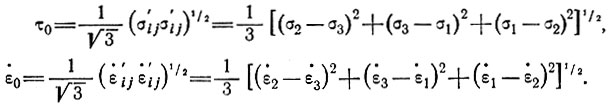
(7)

Заметим, что

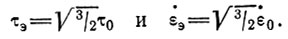
Отсюда максимальное напряжение сдвига и скорости деформации выразим через

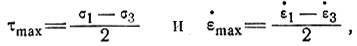
(8)

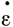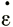где σ₁, σ₃, ₁, ₃ - соответственно максимальные и минимальные главные напряжения и скорости деформации.

Определим теперь эти обобщенные напряжения сдвига применительно к некоторым обычным ситуациям.

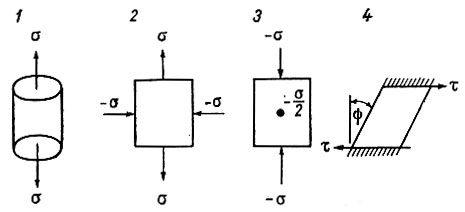
1 - растяжение в одном измерении со сжатием в двух других, 2 - чистый сдвиг (в двух измерениях), 3 - чистый сдвиг плюс гидростатическое давление (в двух измерениях), 4 - простой сдвиг

1. При простом растяжении имеем главные напряжения (σ, 0, 0), гидростатическое давление р = σ/3 и σ'_ij =(2σ/3, -σ/3, -σ/3). Отсюда

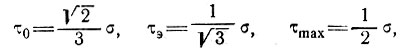
или

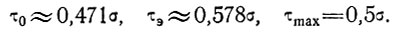
При этом виде растяжения главные скорости деформации равны (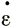, -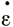/2, -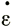/2). Следовательно,

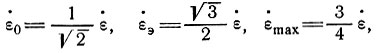
или

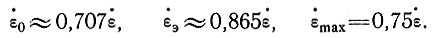
Заметим, что эффективное напряжение сдвига больше, чем максимальное напряжение сдвига, и, таким образом, оно не может соответствовать действительному напряжению сдвига в теле ледника.

2. Для чистого сдвига в двух измерениях при нулевом гидростатическом давлении главные напряжения сдвига равны (σ, 0, -σ), кроме того р = 0, а σ'_ij = (σ, 0, -σ). Следовательно,

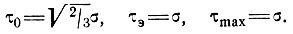
Поскольку главные скорости деформации составляют (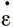, 0, -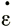), то

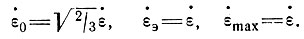
3. Деформация, состоящая из простого сжатия с движением, ограниченным двумя измерениями, эквивалентна чистому сдвигу (σ/2, 0, -σ/2) типа 2 плюс гидростатическое давление (-σ/2).

Если главными напряжениями являются (σ, σ/2, 0), р = σ/2, σ_ij = (σ/2, 0, -σ/2), то

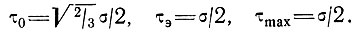
Если главные скорости деформации равны (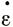, 0, -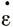), то

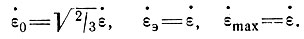
4. Деформация "простой сдвиг" соответствует типичному градиенту горизонтальной скорости деформации по глубине в массе льда, фиксированной у основания, т. е.

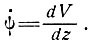
При этом главные напряжения оказываются такими же, как и для чистого сдвига, а именно (τ, 0, -τ), р = 0.

Поэтому

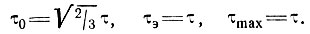
Так как главные скорости деформации равны 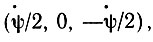, то

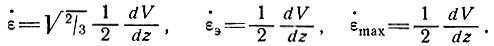
Поскольку эффективное напряжение сдвига равно напряжению сдвига при простом сдвиге и является постоянным коэффициентом, который при более сложных напряженных состояниях умножается на октаэдрическое напряжение сдвига, то термин "напряжение сдвига" (τ) будет принят в дальнейшем для обозначения указанного эффективного напряжения сдвига без более точного определения. Аналогично поступим и со скоростью деформации сдвига .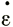

Из уравнений (5) и (6) Най [86] получил связь между напряжением и скоростью деформации сдвига

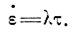
(9)

Для данного типа льда I и температуры Т можно ожидать, что функция λ является функцией только напряжения сдвига τ, т. е.

(10)

Тогда для определения закона течения льда необходимо установить значения функции λ, т. е. отношение скорости деформации сдвига к напряжению сдвига, и показать, как эта функция зависит от напряжения, температуры и типа льда, определяемого некоторыми свойствами, такими, как размер кристаллов и их ориентация, плотность и тип пористости.

Поскольку нашей задачей является применение закона течения к изучению динамики больших масс льда, сосредоточим внимание в основном на напряжениях, температурах и типах льда, встречающихся в больших ледниковых массах.