1. Введение

1.1. Постановка задачи

Основная задача при изучении динамики больших естественных масс льда в том, чтобы установить законы, управляющие их движением, и показать, как можно использовать эти законы для расчета современного движения, прошлого и будущего состояния масс льда при минимуме измерений. Эту основную задачу можно разделить на три части - вывод уравнений движения, определение связи между напряжением и деформацией льда и решение уравнений движения для трех типов масс льда.

1.1.1. Уравнения движения. Обозначим составляющие вектора какой-либо точки во льду, имеющем плотность ρ, через х_i (i = 1, ..., 3) в прямоугольных координатах, при этом х₁ - ось, совпадающая с направлением движения в горизонтальной плоскости, х₂ - вертикальная ось, х₃ - нормаль к направлению движения.

Обозначим компоненты тензора напряжений в точке х_i через σ_ij. Внешняя сила, действующая на элементарный объем среды, является силой тяжести ρg_i.

В естественных ледниковых массах вследствие малой скорости деформации под действием силы тяжести ускорения малы, поэтому ими можно пренебречь.

Таким образом, получаем уравнение движения (суммируя по дважды повторяющимся индексам)

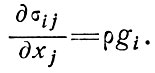
(1)

Вообще, вследствие деформации льда все граничные условия для напряжения неизвестны, тем не менее обычно можно измерить граничные скорости. Поэтому для вывода уравнений движения в терминах скоростей и градиентов скоростей (скоростей деформации) нам нужно знать связь между напряжением и скоростью деформации.

1.1.2. Связь между напряжением и скоростью деформации льда. Практически для большинства целей лед можно считать несжимаемым. Поэтому единственным видом деформации, который представляет для нас интерес, является чистый сдвиг без изменения объема. Пусть ε_ij - тензор скорости деформации в направлении х_i, т. е.

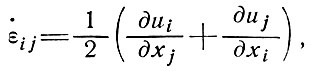
где u_i - скорость в x_i, тогда

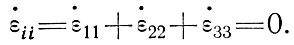
(2)

Особенности связи между напряжением и скоростью деформации, характерные для закона течения льда, будут рассмотрены в разделе 2. А пока можно выразить σ_ij как функцию ε_ij с помощью тензора девиатора напряжения σ'_ij, определяемого как

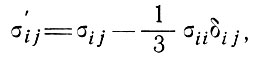
(3)

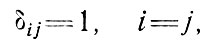
или

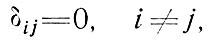
и закона течения льда

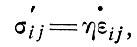
(4)

где η - скалярная функция инвариантов напряжения и других характеристик льда, таких, как температура.

Чтобы решить уравнения (1) и (4) относительно скоростей деформации, необходимо знать граничные скорости деформации, а для решения последних относительно скоростей движения требуется знать граничные скорости.

Эти два положения показывают, что для массы ледника определенной формы и размера (т. е. при известных профилях высоты, ложа и плана) решение относительно скорости движения не является однозначным и зависит от граничной скорости и скорости деформации, которые, как можно ожидать, к тому же вообще изменяются во времени. Тот совершенно особый случай установившегося состояния, при котором размеры границ и скорости движения ледника сохраняются постоянными вследствие особого характера аккумуляции, абляции, обламывания и т. п., будет рассмотрен отдельно.

1.1.3. Решение уравнений движения для различных граничных условий. При изучении динамики естественных масс льда нужно знать их формы и размеры. Для этого необходимо:

1) произвести съемку границ этих масс льда в горизонтальной плоскости (например, методом аэрофотосъемки или наземного тригонометрического наблюдения);

2) установить контуры их высоты методом барометрического или оптического определения уровня, а также фотограмметрированием с самолета или наземными наблюдениями;

3) определить контуры ложа методом сейсмических наблюдений, дополняемых гравитационными или радиолокационными измерениями.

Этого было бы достаточно для расчета напряжения во льду, если бы он был неподвижен, но поскольку лед деформируется, необходимо знать скорости его движения и деформации на границе. Они обычно определяются в нескольких точках методами воздушного или наземного наблюдений.

Исходя из этих граничных условий, по уравнениям движения и закону течения льда можно определить численным интегрированием скорости деформации и движения льда по всей массе ледника. Численный подход, однако, правомерен только в особых случаях. Для уяснения общих принципов динамики масс льда в работе предпринята попытка исследовать аналитические решения скорости для некоторых общих типов масс льда.

Необходимость знать граничные значения скорости движения льда и деформации и их следствия заслуживает особого внимания. Было проведено несколько исследований изменения скорости, формы и размера ледниковых масс во времени в зависимости от изменения скорости аккумуляции. Но даже если скорость аккумуляции остается постоянной, можно ожидать, что форма, размер и распределение скорости движения будут изменяться во времени, по- видимому, колеблясь вокруг некоторых "равновесных значений", которые "устанавливаются" лишь на очень короткое время.